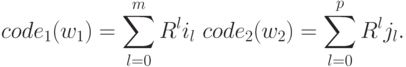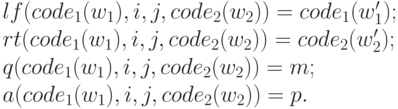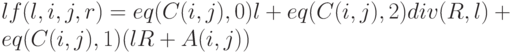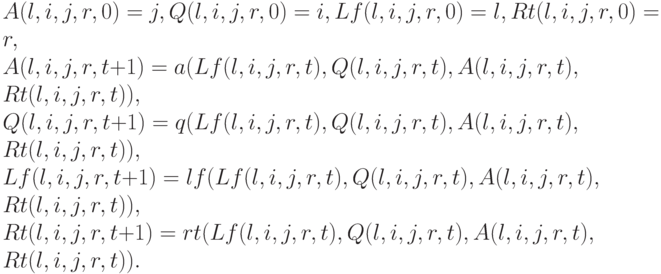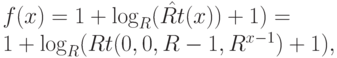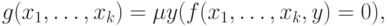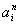Частично рекурсивные функции машина тьюринга
Вычислимые функции, тезис Тьюринга-Черча и неразрешимые проблемы
Частичная рекурсивность функций, вычислимых по Тьюрингу
В этом параграфе покажем, как можно промоделировать работу машины Тьюринга, используя частично рекурсивные определения.
Пусть при i >= k или j >= R эти функции принимают какое-нибудь фиксированное значение (например, 0). Тогда по лемме 18.1 все они примитивно рекурсивны.
и следовательно, функция f(x) частично рекурсивна.
Тезис Тьюринга-Черча и алгоритмически неразрешимые проблемы
Мы рассмотрели три математические модели для описания алгоритмов и вычисляемых ими функций, отражающие различные аспекты и представления о работе абстрактного вычислителя. Из теорем 8.1, 10.2 и 10.3 непосредственно получаем
Естественно, возникает вопрос о том, насколько общим является этот результат? Верно ли, что каждый алгоритм может быть задан одним из рассмотренных способов? На эти вопросы теория алгоритмов отвечает следующей гипотезой.
Чтобы показать связь теории алгоритмов с «практическим» программированием, рассмотрим некоторые алгоритмичские проблемы, связанные со структурированными программами.
Рекурсивные функции
Машины Тьюринга и рекурсивные функции
Мы рассмотрели несколько различных приемов построения примитивно рекурсивных функций. Тем не менее остается не вполне ясным, насколько этот класс широк. Сейчас мы покажем, что он включает в себя все достаточно быстро вычислимые функции.
При имитации работы машин Тьюринга с помощью программ мы кодировали состояние машины четырьмя числами (код левой части ленты, код правой части ленты, состояние и буква под головкой). При этом удобно было такое кодирование : левую часть ленты мы считали записью числа в системе счисления, в которой основание равно числу символов в алфавите машины, а пробел считается нулем; с правой частью ленты мы поступали так же, только в обратном порядке (младшие разряды у головки). При этом добавление или изъятие символа у головки соответствовало простой арифметической операции (удаление это деление нацело, добавление умножение на основание системы счисления и сложение ). При таком кодировании функции перехода (четыре функции четырех аргументов, показывающие следующее состояние как функцию предыдущего), записываются простыми формулами и примитивно рекурсивны.
87. Сформулируйте и докажите соответствующее утверждение.
Частично рекурсивные функции
Часто используется обозначение
и потому оператор минимизации также называют 
Функции, получающиеся из базисных (нуля, проекции и прибавления единицы) с помощью операторов подстановки, примитивной рекурсии и минимизации, называются частично рекурсивными. Если такая функция оказывается всюду определенной, то ее называют общерекурсивной функцией.
Верно и обратное: Теорема 77. Всякая частично рекурсивная функция вычислима на машине Тьюринга.
Поэтому если мы верим в » тезис Тьюринга», гласящий, что всякая вычислимая функция вычислима на машине Тьюринга, то должны верить и в » тезис Черча» (всякая вычислимая функция частично рекурсивна), так что эти тезисы равносильны.
Параллельно английский математик Тьюринг и американский математик Пост предложили свои модели абстрактных вычислительных машин (машины Тьюринга и Поста), отличающиеся лишь некоторыми деталями, и высказали предположение о том, что такие машины покрывают весь класс алгоритмических процессов. Вскоре стало ясно, что вычислимость функции на таких машинах равносильна частичной рекурсивности. (Исторические подробности можно узнать из книги Клини [4].)
Так или иначе, сейчас выражения » тезис Тьюринга», » тезис Черча», » тезис Поста» и т.п. обычно употребляют как синонимы: эти тезисы утверждают, что интуитивно понимаемый класс вычислимых частичных функций совпадает с формально определенным классом частично рекурсивных функций (тезис Черча), вычислимых на машинах Тьюринга функций (тезис Тьюринга) и т.д. При таком понимании можно доказать равносильность всех этих тезисов, так как все известные формальные определения вычислимости (частичная рекурсивность, машины Тьюринга и т.д.) приводят к одному и тому же классу функций.
Алгоритмы. Машина Тьюринга. Альтернативные определения алгоритма. Теория вычислимости и проблема останова.
Мы часто решаем задачи различной сложности: бытовые, математические, и т.п. Некоторые решаются легко, над некоторыми приходится изрядно подумать, для некоторых мы так и не находим решения.
В общем случае, способ решения задачи (если оно есть) можно описать с помощью конечного числа элементарных действий.
Например, решение квадратного уравнения:
Можно ввести следующее интуитивное понятие алгоритма:
Алгоритм набор инструкций, описывающих порядок действий исполнителя для достижения результата решения задачи за конечное число действий, при любом наборе исходных данных.
Это, конечно, не строгое определение, но оно описывает суть понятия алгоритма.
Алгоритмы составляются в расчёте на конкретного исполнителя, и, соответственно, должны быть составлены на языке, который исполнитель сможет понять.
Исполнителем алгоритма может быть человек, а может быть и вычислительная машина, или какой-нибудь другой автомат, например, ткацкий станок.
Выделяются следующие свойства алгоритмов:
Дискретность алгоритм должен представлять собой некую последовательность отдельных, чётко определённых шагов (действий). Каждое из этих действий должно быть конечно по времени. Детерминированность на каждом шаге работы алгоритма, следующий шаг однозначно определяется текущим состоянием системы. Как следствие, на одинаковых исходных данных, алгоритм всякий раз возвращает одинаковые результаты, сколько бы раз его ни выполняли. Понятность алгоритм должен быть сформулирован на языке, понятном исполнителю. Если речь идёт о вычислительной машине, алгоритм должен использовать только те команды, которые известны вычислительной машине и результат действий которых строго определён. Конечность алгоритм должен завершаться за конечное число шагов. Массовость алгоритм должен быть применим к разным наборам входных данных. Другими словами, алгоритм должен быть пригоден для решения класса задач. Возвращаясь к примеру с квадратным уравнением, алгоритм подходит для решения всех квадратных уравнений, а не только одного или нескольких. Результативность алгоритм должен завершаться определенным результатом. Скажем, решением задачи, или выяснением отсутствия решений. Если алгоритм не приводит к результату, непонятно, зачем он вообще такой нужен.
Не всякий способ решения задачи является алгоритмом. Скажем, алгоритм подразумевает отсутствие выбора. Например, большинство кулинарных рецептов алгоритмами не являются, поскольку используют такие фразы как “соль добавить по вкусу”. Как следствие, нарушается требование детерминированности.
Не для каждой задача, для которой существует решение, существует так же и алгоритм решения. Например, задача распознавания изображений до сих пор в значительной мере остается не решенной, и уж точно не с помощью строгого алгоритма. Впрочем, использование нейросетей дает вполне неплохие результаты.
Обычно, для алгоритма существуют наборы допустимых входных данных. Было бы странно пытаться применить алгоритм решения уравнений для приготовления ужина, или наоборот.
Кроме того, ограничен так же и набор возможных действий исполнителя, поскольку если бы были допустимы любые действия, то среди них должно было бы быть так же и “недопустимое”.
Строгое определение алгоритма
Определение алгоритма, приведенное выше, не является строгим. Это создает некоторые трудности. В частности, с таким определением невозможно строго доказать, является ли данный класс задач решаемым при помощи алгоритма.
Оказывается, существует класс алгоритмически неразрешимых задач – задач, для которых невозможно составить алгоритм решения. Но чтобы строго доказать алгоритмическую неразрешимость, нужно для начала иметь строгое определение алгоритма.
В 20-30 годах XX века, над проблемой строгого определения алгоритма работали разные математики, в частности Алан Тьюринг, Эмиль Леон Пост, Андрей Андреевич Марков, Андрей Николаевич Колмогоров, Алонзо Чёрч и другие. Их работа в итоге привела к возникновению и развитию теории алгоритмов, теории исчислимости и различных подходов к исчислению, и, кстати, программированию в целом. Одним из результатов их работы стало появление нескольких строгих определений алгоритма, введенных различным образом, но эквивалентных друг другу.
Мы подробно остановимся на определении Тьюринга, и поверхностно разберем эквивалентные определения Поста, Чёрча и Маркова.
Машина Тьюринга
Для введения формального определения алгоритма, Тьюринг придумал и описал абстрактную вычислительную машину, называемую вычислительной машиной Тьюринга, или просто машиной Тьюринга.
Английский математик, логик, криптограф, возможно первый в мире “хакер”, стоял у истоков информатики и теории искуственного интеллекта. Внес существенный вклад в победу союзных войск во второй мировой войне.
В качестве входных данных для машины Тьюринга используются слова, составленные с помощью некоего алфавита, то есть, набора символов.
Результатом работы машины Тьюринга так же являются слова.
Слово, к которому применяется алгоритм, называется входным. Слово, которое получается в результате работы, выходным.
Набор слов, к которым применим алгоритм, называется областью применимости алгоритма.
Строго говоря, доказать, что любой объект может быть представлен в виде слов, составленных в каком-то алфавите, нельзя – для этого нам бы потребовалось строгое определение объекта. Однако, можно проверить, что любой наугад взятый алгоритм, работающий над объектами, можно преобразовать так, что он будет работать над словами, при этом суть алгоритма не изменится.
Описание машины Тьюринга
В состав машины Тьюринга входит неограниченная в обе стороны лента, разделенная на ячейки, и управляющее устройство (также называется головкой записи-чтения, или просто автомат), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Хотя машина Тьюринга является абстрактной концепцией, достаточно просто представить себе подобную машину (правда, с конечной лентой), и даже существуют демонстрационные машины в таком роде:
Алгоритм для машины Тьюринга удобно представлять в виде таблицы: столбцы таблицы соответствуют текущему (наблюдаемому) символу на ленте, строки – текущему состоянию автомата, а в ячейках записывается команда, которую должен выполнить автомат.
Команда, в свою очередь, может иметь следующую структуру:
\[ a_k \left\lbrace \begin
Пример
Составим алгоритм для машины Тьюринга, который прибавит к входному слову, представляющему собой десятичное число, 1.
Будем считать, что в начальном состоянии автомат находится слева от входного слова.
Тогда, описательно, алгоритм можно сформулировать следующим образом:
Условимся, что начальное состояние \(1\) – поиск начала входного слова, \(2\) – поиск конца входного слова, \(3\) – прибавление 1.
| \(_ | Λ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ΛП1 | 0Н2 | 1Н2 | 2Н2 | 3Н2 | 4Н2 | 5Н2 | 6Н2 | 7Н2 | 8Н2 | 9Н2 |
| 2 | ΛЛ3 | 0П2 | 1П2 | 2П2 | 3П2 | 4П2 | 5П2 | 6П2 | 7П2 | 8П2 | 9П2 |
| 3 | 1Н0 | 1Н0 | 2Н0 | 3Н0 | 4Н0 | 5Н0 | 6Н0 | 7Н0 | 8Н0 | 9Н0 | 0Л3 |
Проследим работу этого алгоритма на примере. Первая строчка соответствует ленте, во второй обозначается положение автомата и его текущее состояние.
В состоянии 1, автомат находится над пустой ячейкой. Соответствующая команда из таблицы “ΛП1”, то есть, оставить ячейку пустой, переместиться вправо и остаться в состоянии 1:
Теперь автомат наблюдает значение “1”. Соотвествующая команда “1Н2”, то есть оставить в ячейке “1”, не перемещаться, и перейти в состояние “2”:
В состоянии “2”, автомат наблюдает значение “1”. Соответствующая команда “1П2”, то есть оставить “1”, переместиться вправо и остаться в состоянии “2”:
Аналогично, команда для состояния “2” и символа “9” – “9П2”:
Наконец, в состоянии 2 автомат наблюдает пустой символ. Команда “ΛЛ3”:
Теперь, в состоянии 3 и наблюдая символ “9”, автомат выполняет команду “0Л3”:
Наконец, выполняется команда “2Н0”:
Состояние “0” – состояние остановки. Работа алгоритма завершена.
Формальное описание
Математически, машину Тьюринга можно описать следующим образом:
Ключевым в теории алгоритмов является тезис Тьюринга.
В вольной формулировке, тезис Тьюринга формулируется следующим образом:
Тезис Тьюринга для любой алгоритмически разрешимой задачи, существует решающая эту задачу машина Тьюринга. иначе, для любого алгоритма существует эквивалентная ему машина Тьюринга.
Тезис Тьюринга позволяет говорить об алгоритмах, пользуясь достаточно простым математическим аппаратом. Более того, сама по себе машина Тьюринга является универсальным исполнительным устройством, и сама возможность создания такой воображаемой машины стала поводом говорить о создании универсальной вычислительной техники.
Альтернативные определения алгоритма
Кроме машины Тьюринга, существует несколько независимых определений, эквивалентных определению Тьюринга.
В частности, определение через машину Поста, через лямбда-исчисление Чёрча, нормальный алгоритм Маркова.
Рассмотрим эти способы.
Машина Поста
Через год после Тьюринга, американский математик Эмиль Леон Пост независимо предложил другую абстрактную универсальную вычислительную машину, которая является некоторым упрощением по сравнению с машиной Тьюринга.
Машина Поста оперирует двузначным алфавитом, и внутреннее состояние автомата заменяется на строку программы.
В остальном, машина Поста аналогична машине Тьюринга: есть автомат, и есть бесконечная лента с ячейками.
Машина Поста может выполнять следующие команды:
Так же машина Поста имеет несколько запрещенных команд:
Подобные события приводят к аварийному завершению работы.
Для написания программ для машины поста можно использовать следующие обозначения:
Эта программа сотрет первую метку (1), находящуюся справа от начального положения автомата, и остановит автомат в ячейке слева от нее.
По большому счету, машина Поста является предшественником императивных языков программирования, например, C, Fortran и пр.
Машина Поста является эквивалентной машине Тьюринга. Другими словами, для любой программы для машины Тьюринга, можно записать эквивалентную программу для машины Поста, и наоборот.
Одним из важных следствий этой эквивалентности является то, что любой алфавит можно свести к двоичному коду.
Аналогично тезису Тьюринга, существует так же и тезис Поста.
Тезис Поста всякий алгоритм представим в виде машины Поста.
Нормальный алгоритм Маркова
Нормальные алгоритмы Маркова предназначены для применения к словам в различных алфавитах.
Определение всякого нормального алгоритма состоит из двух частей:
Сам алгоритм применяется к словам, то есть последовательностям символов алфавита.
При этом предполагается, что вспомогательные символы \(\to\) и \(\to\cdot\) не принадлежат алфавиту алгоритма.
Процесс применения нормального алгоритма к произвольному слову \(V\) представляет собой следующую последовательность действий:
Любой нормальный алгоритм эквивалентен некоторой машине Тьюринга, и наоборот – любая машина Тьюринга эквивалентна некоторому нормальному алгоритму.
Аналог тезиса Тьюринга для нормальных алгоритмов принято называть принципом нормализации.
Пример
Данный алгоритм преобразует двоичные числа в “единичные” (в которых записью целого неотрицательного числа N является строка из N палочек). Например, двоичное число 101 преобразуется в 5 палочек: |||||.
Рекурсивные функции
Систему, эквивалентную машине Тьюринга, можно построить на основе математических функций. Для этого, нам требуется ввести следующие классы функций:
Последний класс будет совпадать с классом вычислимых по Тьюрингу функций (то есть функций, для вычисления которых можно построить алгоритм для машины Тьюринга).
Определение алгоритма через рекурсивные функции по сути лежит в основе лямбда-исчисления, и на его основе строится подход функционального программирования.
Примитивно рекурсивные функции
Класс примитивно рекурсивных функций содержит базовые функции и все функции, получающиеся из базовых посредством операторов подстановки и примитивной рекурсии.
К базовым функциям относятся:
Для конструирования остальных функций класса используются операторы:
Частично рекурсивные функции
Класс частично рекурсивных функций включает примитивно рекурсивные функции, и, плюс к этому, все функции, которые получаются из примитивно рекурсивных с помощью оператора минимизации аргумента:
Оператор минимизации аргумента
\[ h(x_1,\ldots,x_
В то время как примитивно рекурсивные функции всегда вычислимы, частично рекурсивные функции при некоторых значениях аргументов могут быть не определены.
Более строго частично рекурсивные функции следовало бы называть “частично определенные рекурсивные функции”, поскольку они определены только на части возможных значений аргументов.
Общерекурсивные функции
Общерекурсивные функции – это подкласс всех частично рекурсивных функций, которые определены для любых значений аргументов. Задача определения того, является ли данная частично рекурсивная функция общерекурсивной является алгоритмически неразрешимой. Это подводит нас к теме теории вычислимости и проблеме останова.
Теория вычислимости и проблема останова
Наше воображение в целом допускает существование неразрешимых задач, то есть задач, для решения которых невозможно составить алгоритм.
Исследованием таких задач занимается теория вычислимости.
Примерами алгоритмически неразрешимых задач являются проблема останова и проблема распознавания выводимости. Рассмотрим их более подробно.
Проблема останова является алгоритмически неразрешимой. Докажем это.
Пусть существует универсальный алгоритм, решающий проблему останова. Рассмотрим тогда класс алгоритмов, обрабатывающий тексты описания алгоритмов.
Более общей формулировкой проблемы останова является проблема определения выводимости.
Проблема распознавания выводимости
Пусть определены некий алфавит, слова (формулы) этого алфавита, и система формальных преобразований над словами этого алфавита (т.е. построено логическое исчисление)
Существует ли для любых двух слов \(R\) и \(S\) дедуктивная цепочка, ведущая от \(R\) к \(S\) в рамках данного логического исчисления?
В 1936 году Алонзо Чёрч доказал теорему Чёрча.
Теорема Чёрча Проблема распознавания выводимости алгоритмически неразрешима.
Чёрч использовал для доказательства формализм лямбда-исчисления. В 1937 независимо от него ту же теорему доказал Тьюринг, используя формализм машины Тьюринга.
Поскольку все определения алгоритмов эквиваленты друг другу, существует система понятий, не связанная с конкретным определением алгоритма, и оперирует понятием вычислимой функции.
Вычислимая функция функция, для вычисления которой можно составить алгоритм.
Существуют задачи, в которых связь между входными и выходными данными невозможно описать с помощью алгоритма. Такие функции являются невычислимыми.
Пример невычислимой функции
Тема 9 Элементы теории алгоритмов
9.1 Машины Тьюринга
9.2 Рекуррентные функции
9.3 Тезисы Тьюринга и Чёрча
Понятие алгоритма стихийно формировалось с древнейших времен. Современный человек понимает под алгоритмом четкую систему инструкций о выполнении в определенном порядке некоторых действий для решения всех задач какого-то данного класса.
Многочисленные и разнообразные алгоритмы окружают нас буквально во всех сферах жизни и деятельности.
Большое количество алгоритмов встречаются при изучении математики буквально с первых классов школы. Это, прежде всего, алгоритмы выполнения четырех арифметических действий над различными числами – натуральными, целыми, дробными, комплексными. Примерами известных алгоритмов являются алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел, вычисление определителей различных порядков, вычисление рангов матриц с рациональными элементами, приближенное вычисление корней уравнений и т. д.
В начале ХХ века у математиков начали возникать подозрения в том, что некоторые массовые задачи, по-видимому, не имеют алгоритмического решения. Для точного доказательства несуществования алгоритма необходимо иметь его точное математическое определение. Первые работы по уточнению понятия алгоритма и его изучению были выполнены в 1936–1937 гг. А. Тьюрингом, Э. Постом, К. Геделем, А. А. Марковым, А. Черчем. Было выработано несколько определений понятия алгоритма, но впоследствии выяснилось, что все они равносильны между собой, то есть определяют одно и то же понятие.
9.1 Машины Тьюринга. Машины Тьюринга есть математическая (вообразимая) машина, а не машина физическая. Она есть такой же математический объект, как функция, производная, интеграл и т. д. А так же, как и другие математические понятия, понятие машина Тьюринга отражает объективную реальность, моделирует некие реальные процессы.
Машина Тьюринга состоит из ленты, управляющего устройства и считывающей головки.
Лента разбита на ячейки. Во всякой ячейки в каждый момент времени находится в точности один символ из внешнего алфавита А=<а0,а1,…аn-1 >, n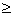
Считывающая головка перемещается вдоль ленты так, что в каждый момент времени она обозревает ровно одну ячейку ленты. Головка может считывать содержимое обозреваемой ячейки и записывать в нее вместо обозреваемого символа некоторый новый символ из внешнего алфавита.
Работа машины Тьюринга определяется программой. Программа состоит из команд. Каждая команда представляет собой выражение одного из следующего вида:
Команда 1 заключается в том, что содержимое aj обозреваемой на ленте ячейки стирается, а на его места дописывается символ ae (который может совпадать с aj ), машина переходит в новое состояние qk (оно может совпадать с предыдущим состоянием qi ).
Команда 2 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю справа ячейку.
Команда 3 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю слева ячейку.
Если считывающая головка находится в крайней справа (слева) ячейки ленты и происходит ее сдвиг вправо (влево), то к ленте пристраивается новая ячейка в пустом состоянии.
Машинным словом или конфигурацией называется слово вида
Где аij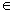
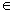

Например, конфигурация 13q10212 на ленте выглядит следующим образом: