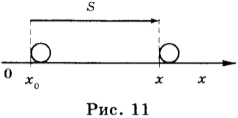
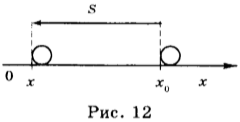
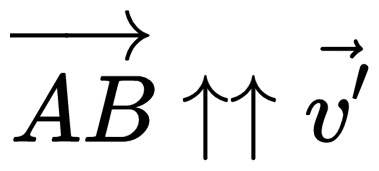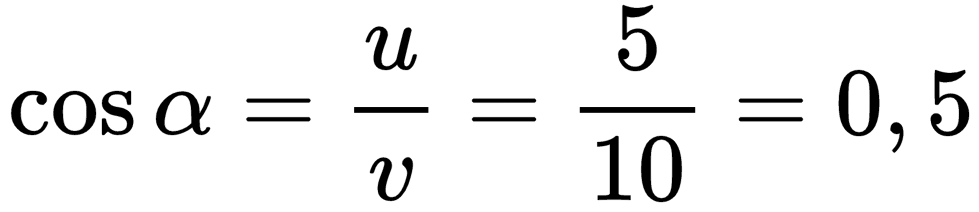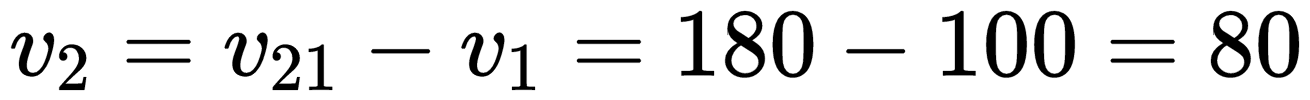Чему равна относительная скорость автомобилей движущихся навстречу друг другу по прямолинейному
Относительная скорость.
Относительная скорость – это физическая величина, равная векторной разности скоростей, заданных относительно неподвижной системы отсчета.
При изучении механического движения в первую очередь подчеркивается его относительность. При изучении различных свойств движения тела предполагается, что рассматривается абсолютное движение (т. е. движение, отнесенное к неподвижным осям). Во многих случаях возникает необходимость определить относительное движение, отнесенное к системе отсчета, движущейся по отношению к неподвижным осям.
Относительное движение точки по отношению к подвижной системе отсчета может рассматриваться как абсолютное движение, и обладает всеми свойствами абсолютного движения.
Движение можно рассматривать в разных системах отсчета. Выбор системы отчета диктуется удобством: ее нужно выбрать так, чтобы изучаемое движение и его закономерности выглядели по возможности проще. Для перехода от одной системы отсчета к другой необходимо знать, какие характеристики движения изменяются и каким образом, а какие остаются неизменными.
Исходя из опытов можно утверждать, что при рассмотрении движений, происходящих со скоростями, малыми по сравнению со скоростью света, время неизменно во всех системах отсчета, что означает, что при измерении в любой системе отсчета промежуток времени между двумя событиями одинаков.
Что же касается пространственных характеристик, то положение тела изменяется при переходе к другой системе отсчета, однако при этом не меняется пространственное расположение этих двух событий.
Теперь рассмотрим изменение скорости движения тел при переходе от одной системы отсчета к другой, которая движется относительно первой.
Рассмотрим пример переправы на пароме, движущемся поступательно относительно берегов (относительно земли). Вектор перемещения пассажира относительно берегов обозначим через Δr, а относительно парома – через Δr´. Перемещение парома относительно земли за то же время Δt обозначим через ΔR. В этом случае
Разделим равенство почленно на промежуток времени Δt, в течение которого произошли эти перемещения. Перейдя к пределу Δt >0, получим аналогичное соотношение для скоростей:
Из формулы (2) следует, что относительная скорость двух тел одинакова во всех системах отсчета. При переходе к новой системе отсчета к скорости каждого тела прибавляется один и тот же вектор V скорости системы отсчета. Поэтому разность векторов скоростей тел υ – υ´ не изменяется. Относительная скорость тел абсолютна.
10 класс
§ 10. Относительность механического движения. Закон сложения скоростей
Относительность движения.
Ранее для описания механического движения тела мы ввели понятие системы отсчёта. Дело в том, что не имеют определённого смысла слова «тело движется». Нужно обязательно сказать, по отношению к каким телам или относительно какой системы отсчёта это движение рассматривается. Например, пассажиры движущегося поезда неподвижны относительно стен вагона. И в то же время те же пассажиры движутся в системе отсчёта, связанной с Землёй. Таким образом, скорость одного и того же тела различна в разных системах отсчёта.
При решении конкретной задачи мы можем выбрать ту или иную систему отсчёта. Но среди этих систем отсчёта можно найти наиболее удобные, в которых движение выглядит проще. Особенно важен выбор системы отсчёта в космонавтике. Стыковку космических кораблей рассматривают в системе отсчёта, связанной с одним из кораблей. При выводе корабля на орбиту удобно использовать систему отсчёта, связанную с Землёй. Полёт межпланетных станций изучают в системе отсчёта, связанной с Солнцем и звёздами. Оси координат этой системы отсчёта направлены на удалённые звёзды, а начало координат совмещено с центром Солнца.
Представьте себе пассажира, выпускающего из рук мяч в равномерно движущемся относительно поверхности Земли вагоне. Он видит, как мяч падает относительно вагона вертикально вниз с ускорением. Свяжем с вагоном систему координат X1O1Y1 (рис. 2.46).
В этой системе координат за время падения мяч пройдёт путь AD = h, и пассажир отметит, что мяч упал на пол со скоростью 1 направленной вертикально вниз.
А что же увидит наблюдатель, находящийся на неподвижной платформе, с которой связана система координат XOY? Он заметит (представим себе, что стены вагона прозрачны), что траекторией мяча является парабола AD, и мяч упал на пол со скоростью 2, направленной под углом к горизонту (см. рис. 2.46). Итак, наблюдатели в системах координат X1O1Y1 и XOY обнаруживают различные по форме траектории, скорости и пройденные пути при движении одного тела — мяча.
Такие кинематические понятия, как траектория, координаты, путь, перемещение, скорость, при переходе от одной системы отсчёта к другой могут измениться. В этом и состоит относительность движения, и в этом смысле механическое движение всегда относительно.
Преобразования Галилея и их следствия.
Для проекций на ось X можно записать:
Координаты y, z и yl, zl одинаковы в обеих системах отсчёта. При этом считается, что время течёт одинаково в системах отсчёта К и K1, так что t = t1. Выражения (1) или (2) вместе с утверждением о независимости течения времени от движения (t = t1) называют преобразованиями Галилея. Преобразования координат при переходе от системы отсчёта K1 к системе отсчёта К будут иметь вид (с учётом того, что uх = u):
Закон сложения скоростей.
Учитывая, что = 1 + t, получим
Часто для большей наглядности и удобства используют понятия абсолютного, относительного и переносного движений. Для этого одну из систем координат, например XOY, считают условно неподвижной. Движение тела относительно неподвижной системы координат называют абсолютным. Движение тела относительно подвижной системы координат (относительно X1O1Y1) называют относительным. Движение подвижной системы координат относительно неподвижной называют переносным. Скорость, ускорение, перемещение, путь и траекторию тела в неподвижной системе координат называют абсолютными, а в подвижной системе — относительными. В формуле (4) — абсолютная скорость ( a), 1 — относительная скорость ( отн) — переносная скорость ( п). C учётом этого закон сложения скоростей (4) можно записать в виде:
Абсолютная скорость равна векторной сумме относительной и переносной скоростей.
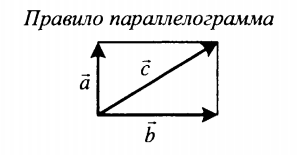
Закон сложения скоростей (5) геометрически осуществляется по правилу параллелограмма (рис. 2.48, а) или треугольника (рис. 2.48, б).
В заключение отметим, что, если одна система отсчёта движется относительно другой равномерно и прямолинейно, ускорения тела в них одинаковы.
Вопросы:
1. В чём состоит относительность механического движения? Приведите примеры.
2. Что называют преобразованиями Галилея?
3. Как связаны между собой скорости тела в различных системах отсчёта, → движущихся относительно друг друга с постоянной скоростью и 2
4. Какой физический смысл имеет:
в) переносная скорость?
5. Каким соотношением связаны данные физические величины?
Вопросы для обсуждения:
1. Пассажир перемещается вдоль палубы корабля, движущегося по реке. Какие из физических величин — перемещение пассажира, скорость его движения, длина палубы, промежуток времени — имеют одинаковые значения в системе отсчёта, связанной с берегом реки?
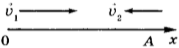
2. Чему равна относительная скорость автомобилей, движущихся навстречу друг другу по прямолинейному участку дороги?
3. Чему равна относительная скорость автомобилей, движущихся друг за другом по одному прямолинейному участку шоссе, но с разными скоростями?
Упражнения:
1. Пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, видит в течение 10 с встречный поезд, длина которого 290 м. Определите модуль скорости встречного поезда относительно пассажира и относительно Земли.
2. Два поезда идут навстречу друг другу: один со скоростью, модуль которой равен 10 м/с, второй — со скоростью, модуль которой равен 20 м/с. Пассажир второго поезда, длина которого 200 м, замечает, что первый поезд проходит мимо него в течение 20 с. В течение какого времени второй поезд обогнал бы первый, если бы они шли в одном направлении?
3. Вагон поезда, движущийся со скоростью 54 км/ч, был пробит пулей, летевшей перпендикулярно направлению движения вагона. Смещение отверстий в стенках вагона относительно друг друга равно 6 см. Ширина вагона равна 2,4 м. Чему равен модуль скорости пули?
4. Самолёт движется относительно воздуха со скоростью, модуль которой равен 50 м/с. Модуль скорости ветра относительно Земли равен 15 м/с.
Чему равен модуль скорости самолёта относительно Земли, если он движется:
в) перпендикулярно направлению ветра?
5. Лодка, двигаясь перпендикулярно берегу, оказалась на другом берегу через 100 с, на расстоянии 25 м ниже по течению. Ширина реки равна 100 м. Определите модуль скорости лодки и модуль скорости течения реки.
Относительность механического движения
теория по физике 🧲 кинематика
Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Относительность перемещения
Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.
Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.
Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:
Относительность скорости в ПСО и НСО
Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.
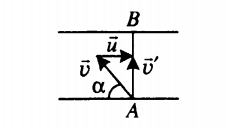
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:
Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):
Косинусу 0,5 соответствует угол, равный 60 градусам.
Относительная скорость двух тел
Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.
Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:
v отн — относительная скорость, или скорость первого тела относительно второго, v 1 и v 2 — скорость первого и второго тела относительно СО.
Варианты обозначения относительной скорости и их проекций:
Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.
Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:
Скорость второго автомобиля относительно дороги равна 80 км/час.
Правила сложения векторов
| Сложение двух сонаправленных векторов | |
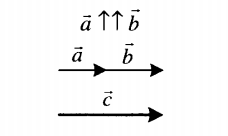 | Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b. |
| Сложение двух противоположно направленных векторов | |
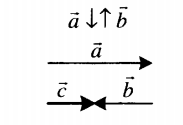 | Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|. |
| Сложение двух векторов, расположенных друг к другу под углом | |
| Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
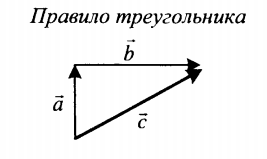 | Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: 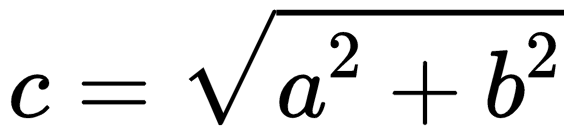 . . |
 | |
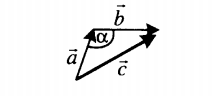 | Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 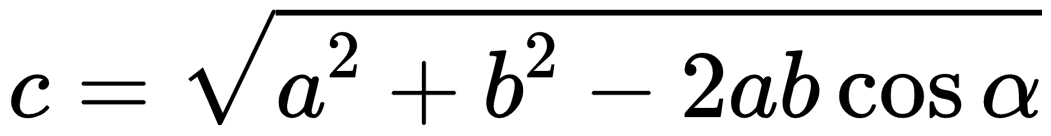 . . |
 | Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: 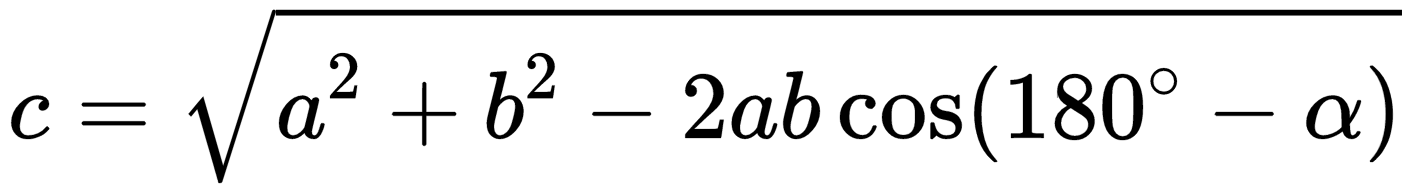 . . |
Правила вычитания векторов
Эта таблица иллюстрирует правила вычитания векторов на примере векторов 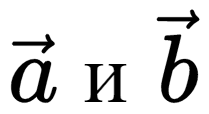
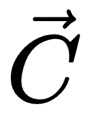
Алгоритм решения
Решение
Записываем данные относительно Земли:
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость второго автомобиля относительно оси ОХ ( v 2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v 1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Записываем закон сложения скоростей в векторном виде:
v ′ — скорость автомобиля относительно земли ( v 1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v 2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50
pазбирался: Алиса Никитина | обсудить разбор | оценить
Равномерное прямолинейное движение
1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.
Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.
2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.
Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.
Если за время \( t \) тело совершило перемещение \( \vec \) , то скорость его движения \( \vec >
3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.
Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.
4. Зависимость координаты от времени можно представить графически.
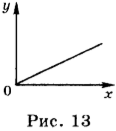
Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: \( x \) = 4 м/с · \( t \) . Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).
Для того чтобы её построить, необходимо иметь две точки: одна из них \( t \) = 0 и \( x \) = 0, а другая \( t \) = 1 с, \( x \) = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.
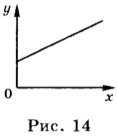
Если в начальный момент времени координата тела \( x_0 \) = 2 м, а проекция его скорости \( v_x \) = 4 м/с, то уравнение движения имеет вид: \( x \) = 2 м + 4 м/с · \( t \) . Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой \( t \) = 0, \( x \) = 2 м (рис. 14).
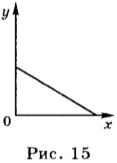
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \) = 2 м – 4 м/с · \( t \) . График зависимости координаты такого движения от времени представлен на рисунке 15.
Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.
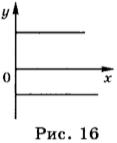
График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.
5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.
Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.
При решении задачи целесообразно придерживаться следующей последовательности действий:
Применим эту последовательность действий к приведённой выше задаче.
Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь
Система отсчёта связана с Землёй, ось \( Ox \) направлена в сторону движения первого тела, начало отсчёта координаты — т. \( O \) — положение первого тела в начальный момент времени.
Начальные условия: \( t \) = 0; \( x_ <01>\) = 0; \( x_ <02>\) = 270.
Уравнения для каждого тела с учётом начальных условий: \( x_1=v_1t \) ; \( x_2=l-v_2t \) . В месте встречи тел \( x_1=x_2 \) ; следовательно: \( v_1t=l-v_2t \) . Откуда \( t=\frac
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?
1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с
2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?
1) 0,25 м
2) 6 м
3) 10 м
4) 150 м
1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)
1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)
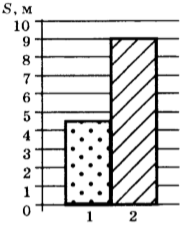
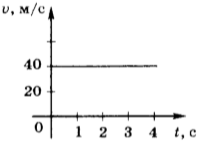
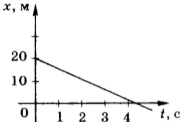
5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен
1) 20 м
2) 40 м
3) 80 м
4) 160 м
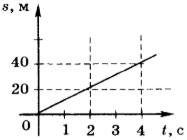
6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен
1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с
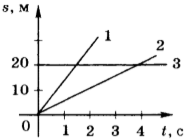
7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости \( v_1 \) , \( v_2 \) и \( v_3 \) движения этих тел.
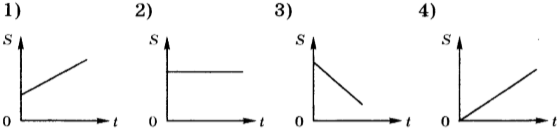
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?
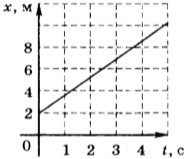
9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?
1) 9,8 м
2) 6 м
3) 4 м
4) 2 м
10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид
1) \( x=1t \) (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)
11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость
ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит
12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.
1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось
Часть 2
13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?