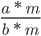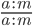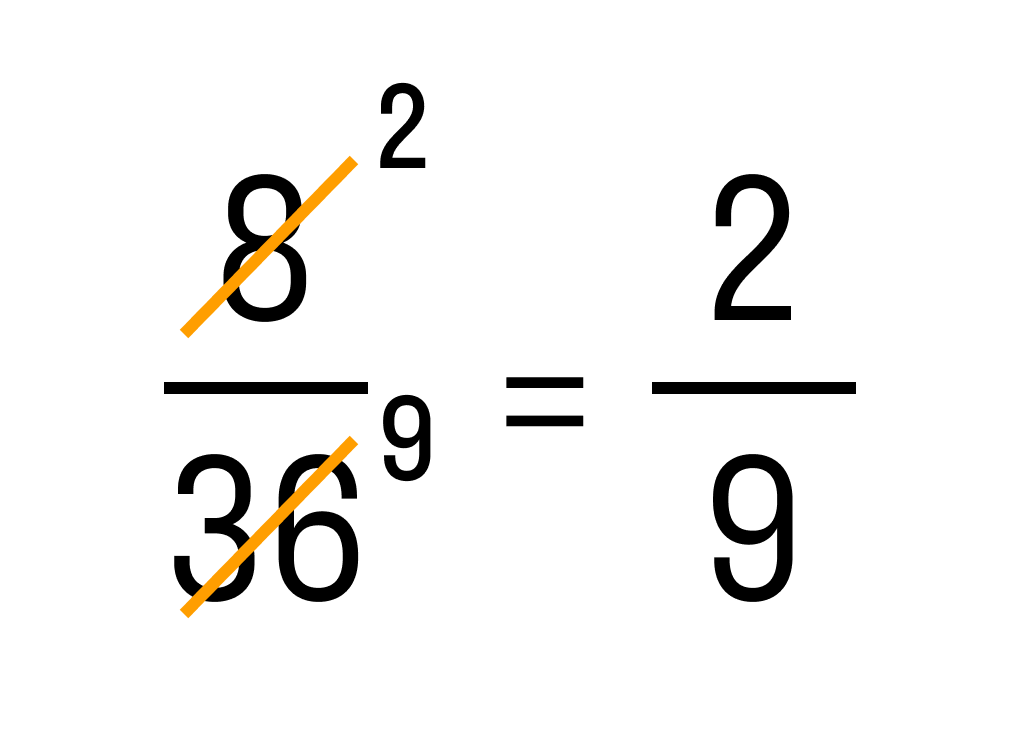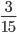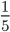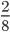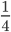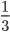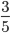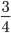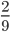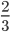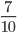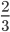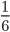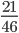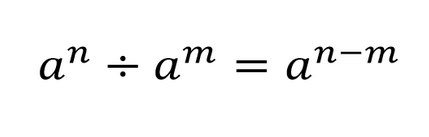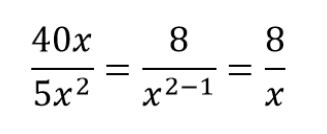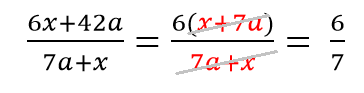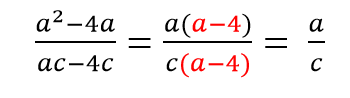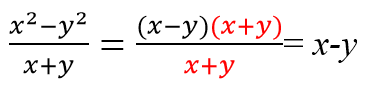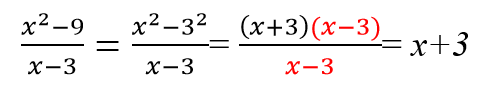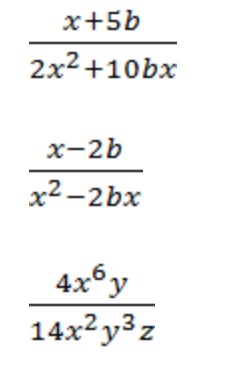Что меняется при сокращении дробей
Как сокращать дроби: простые примеры с подробными решениями
Содержание:
В этой статье коротко предоставим информацию о том, как сокращать дроби. Сначала приведем немного теоретической части, а затем подкрепим ее решением практических задач.
Что означает сократить дробь
Как сокращаются дроби
Как привести дробь к несократимому виду
Обычно алгебраическое решение любой задачи по сокращению дробей сводится к получению равной дроби, но в несокращаемом виде. Чтобы получить несократимую дробь, ее делят на определенное число, которое называется наибольший общий делитель (сокращенно НОД):
Практически рассмотрим, используя дробь \frac < 6 > < 12 >. Ее можно сократить на НОД, который равняется 6. Тогда 6 : 6 = 1 и 12 : 6 = 2. Следовательно:
Последняя дробь является несократимой.
Следует обратить внимание, что в большинстве случаев если требуется выполнить сокращение дробей, то это значит выполнить до получения несократимой дроби.
Как сократить большую дробь
В качестве нового примера возьмем дробь 144192. Сначала найдем наибольший общий делитель для чисел 144 и 192. Для этого можно применить метод разложения на простые множители:
144 : 2 = 72 192 : 2 = 96
72 : 2 = 36 96 : 2 = 48
36 : 2 = 18 48 : 2 = 24
18 : 2 = 9 24 : 2 = 12
Тогда наибольшим общим множителем для данных чисел будет число 48 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 2.
Разделив исходную дробь на 48 получим несократимую дробь:
Разберем еще один способ, который позволяет сокращать числитель и знаменатель дроби последовательно на делитель, который без труда определяется по простейшим математическим признакам. Если требуется сократить дробь типа 40008 800, то можно сразу же определить, что здесь присутствует общий множитель 100, который можно вынести за скобку:
Далее невооруженным глазом заметно, что оба числа делятся на 2, а результат опять на 2 и т. д. В конечном итоге получаем несократимую дробь \frac < 5 > < 11 >= \frac < 4000 > < 8800 >. Теперь можно сказать, что наибольшим общим делителем для данной дроби было число 800.
В заключении заметим, что если знаменатель дроби представляет собой числитель, возведенный в квадрат, то такая дробь в несокращаемом виде всегда будет представлять собой: 1 – в числителе + число, значившееся числителем до сокращения, в знаменателе:
Сокращение обыкновенных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое «сокращение дробей»
Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.
Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.
В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.
С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:


где a, b, m — натуральные числа.
Графически сокращение дробей обычно записывается вот так:
Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.
Больше наглядных примеров и понятных объяснений — на курсах обучения математике в онлайн-школе Skysmart.
Пример 1. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 3.

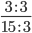
Сокращение выполнено: 
Пример 2. Сократим обыкновенную дробь
Разделим числитель и знаменатель на общий делитель 2.

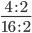
Сокращение выполнено: 
Приведение дробей к несократимому виду
Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.
Так, в результате сокращения в примере 2, мы из дроби 
Выходит, что дробь выдержит еще одно сокращение и придет к виду
Сокращая дробь, стремитесь в итоге получить несократимую дробь.
Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.
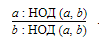
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.
Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.
Пример 3. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 12
Найдем частное: 12 : 12 = 1

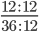
Сокращение выполнено: 
Пример 4. Приведите обыкновенную дробь к несократимому виду
Найдем НОД числителя и знаменателя. НОД = 5
Найдем частное: 15 : 5 = 3

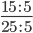
Сокращение выполнено: 
Правило сокращения дробей
Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.
Выполняйте сокращение дробей по следующему алгоритму:
В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.
Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.
Пример 5. Сократите дробь
Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5
Мысленно убираем все общие множители и перемножаем оставшиеся.

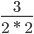
Сокращение выполнено: 
Пример 6. Сократите обыкновенную дробь
Найдем НОД числителя и знаменателя. НОД = 9

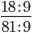
Сокращение выполнено: 
Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.
Пример 6. Сократите дробь:

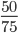
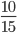
Сокращение выполнено: 
Пример 7. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
168 = 2 * 2 * 2 * 3 * 7
240 = 2 * 2 * 2 * 2 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24
НОД 168 и 240 равен 24
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

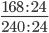
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
360 = 2 * 2 * 2 * 3 * 3 * 5
540 = 2 * 2 * 3 * 3 * 3 * 5
Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180
НОД 360 и 540 равен 180
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

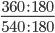
Сокращение выполнено: 
Пример 8. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
420 = 2 * 2 * 3 * 5 * 7
2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7
Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420
НОД 420 и 2520 равен 420
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

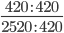
Сокращение выполнено. Дробь приведена к несократимому виду: 
Пример 9. Сократите дробь
Найдем НОД, разложив числитель и знаменатель на простые множители.
1575 = 3 * 3 * 5 * 5 * 7
3450 = 2 * 3 * 5 * 5 * 23
Перемножаем все общие множители между собой 3 * 5 * 5 = 75
НОД 1575 и 3450 равен 72
Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

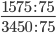
Сокращение выполнено. Дробь приведена к несократимому виду: 
Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.
Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Как сокращать алгебраические дроби?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
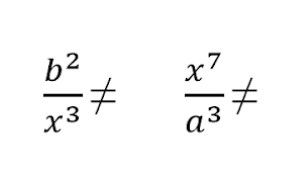 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
Получаем сокращенную дробь.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
Примеры сокращения дробей с помощью формул сокращенного умножения:
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.