Что может быть аргументом функции

Блог Мачула Владимира

Функции представляют собой зависимость одного элемента (результата) от других элементов (аргументов. тех, что внутри :-)). Это как бы понятно. Для того чтобы использовать какую-либо функцию в Excel, следует ввести ее как формулу (нюансы описаны тут) или как часть формулы в ячейку рабочего листа.

Последовательность, в которой должны располагаться применяемые в формуле символы и аргументы, называется синтаксисом функции. Все функции используют одинаковые правила синтаксиса. Если нарушить эти правила, то Excel выдаст сообщение о том, что в формуле имеется ошибка и не будет с вами дружить. Но поверьте, в функциях Excel все достаточно однотипно и разобравшись один раз, на одной-двух функциях, в остальных случаях все будет достаточно просто.

Правила синтаксиса при записи функций

Далее рассмотрены правила, которым необходимо следовать для грамотного и оптимального построения формулы с использованием одной или нескольких функций.

Если функция появляется в самом начале формулы, ей должен предшествовать знак равенства, как это имеет место в начале любой формулы. Я об этом уже говорил в предыдущих статьях, но не грех ещё повторить.

После этого вводится имя функции и сразу за ним – список аргументов в круглых скобках. Аргументы отделяются друг от друга точкой с запятой «;». Скобки позволяют Excel определить, где начинается и где заканчивается список аргументов.

Заметьте, в записи функции обязательно должны присутствовать открывающая и закрывающая скобки, при этом нельзя вставлять пробелы между названием функции и скобками. В противном случае Excel выдаст сообщение об ошибке.

В качестве аргументов можно использовать числа, текст, логические значения, массивы, значения ошибок или ссылки. При этом параметры, задаваемые пользователем, должны иметь допустимые для данного аргумента значения.

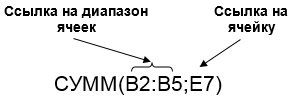
Например, в приведенной ниже формуле осуществляется суммирование значений в ячейках В2, В3, В4, В5 и Е7, причем часть ячеек — от В2 до В5, представлены как непрерывный диапазон.

Рассмотрим работу функции ОКРУГЛ(арг1;арг2), которая возвращает число, округленное до заданного количества знаков после запятой, и имеет два аргумента:

арг1 – адрес ячейки с числом (или само число), которое нужно округлить;

арг2 – количество цифр после запятой у числа после округления.
Чтобы округлить число 2,71828, находящееся в ячейке A1, с точностью до одного, двух или трех знаков после запятой и записать результаты вычислений соответственно в ячейки B1, C1 и D1, необходимо действовать следующим образом.

Аргументы могут быть как константами, так и функциями. Функции, которые являются аргументами другой функции, называются вложенными.

Например, просуммируем значения ячеек А1 и А2, предварительно округлив эти значения до двух десятичных знаков:

Здесь функция ОКРУГЛ является вложенной аж два раза, но это не страшно, в формулах Excel можно использовать до семи уровней вложенности функций.

Стоит отметить, что в Excel существуют функции, которые не имеют аргументов. Примерами таких функций являются ПИ (возвращает значение числа π, округленное до 15 знаков) или СЕГОДНЯ (возвращает текущую дату). При использовании подобных функций следует в строке формул сразу после названия функции ставить пустые круглые скобки без аргументов. Другими словами, чтобы получить в ячейках значение числа p или текущую дату, следует ввести формулы такого вида:

Типы функций Excel

Для удобства работы пользователя при построении формул функции в Excel разбиты по категориям: функции управления базами данных и списками, функции даты и времени, финансовые, статистические, текстовые, математические, логические.

Текстовые функции используются для обработки текста, а именно: поиска нужных символов, записи символов в строго определенное место текста и т.д.

С помощью функций Даты и времени можно решить практически любые задачи, связанные с учетом календарных дат или времени (например, рассчитать число рабочих дней для любого промежутка времени).

Логические функции используются при создании сложных формул, которые в зависимости от выполнения тех или иных условий будут реализовывать различные виды обработки данных. Они особо интересны, и о них поговорим в отдельной статье.

В Excel широко представлены Математические функции и некоторые я уже привел в примерах.

В распоряжении пользователя также находится библиотека Статистических функций, при помощи которой можно осуществлять поиск среднего значения, максимального и минимального элементов и пр.

Источник

Функции

Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.

Функция — это зависимая переменная величина. Аргумент — это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.

Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:

Иногда, чтобы показать, что y зависит от x, пишут просто:

Обратите внимание, что вместо y и x могут использоваться любые другие буквы.

Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:

D(f) — область определения функции
(множество значений аргумента).

E(f) — множество значений функции.

Пример. Возьмём формулу нахождения расстояния по скорости и времени:

где S — это расстояние, v — скорость, а t — время. Если взять скорость, равную 50 км/ч, то каждому неотрицательному значению t будет соответствовать строго определённое значение S:

Источник

Типы аргументов функций

В каждой из функций используется пара скобок. Информация, приведенная в скобках, называется аргументами функции. Количество аргументов в разных функциях не одинаково.

• не иметь ни одного аргумента;
• иметь один аргумент;
• иметь фиксированное количество аргументов;
• иметь неограниченное количество аргументов;
• иметь необязательные аргументы.

Например, функция СЛЧИС, которая возвращает случайное число между нулем и единицей, не имеет аргументов. Но даже при отсутствии аргументов необходимо ввести пустую пару скобок:

Если функция имеет больше одного аргумента, то все они отделяются друг от друга точкой с запятой. В функции НАИБОЛЬШИЙ, которая возвращает n-ое по величине значение из множества данных, используются два аргумента. Первый из них задает диапазон значений, а второй – значение n. Приведенная ниже формула возвращает третье по величине значение ячеек диапазона А1:А100:

Примечание

Символы разделителей определяются в окне региональных стандартов Windows. Если в этом окне установлен русский формат, разделителем списка служит точка с запятой, а десятичным разделителем – запятая. Если же установлен формат США, разделителем списка будет запятая, а десятичным разделителем – точка. Переключите формат в Windows, и вы увидите, что символы разделителей в формулах автоматически изменятся. Кроме разделителей, установленный формат влияет на отображение дат, времени, денежных значений и т.д.

В помощь пользователям, работавшим в Lotus 1-2-3

Если вам приходилось работать в одной из версий Lotus 1-2-3 (или Quattro Pro компании Corel), то вы, наверное, помните, что в этих электронных таблицах перед именем функции должен стоять символ @. Программа Excel способна распознать функцию и без отличительного символа.

От старых привычек трудно избавиться, и поэтому Excel воспринимает символы @ при вводе формул. Как только вы введете формулу, символ @ будет удален.

В качестве оператора ссылки на диапазон в Lotus 1-2-3 и Quattro Pro используются две точки (..), например A1..A10. Excel позволяет использовать такой оператор при вводе формулы. Однако как только формула будет введена, Excel заменит его собственным оператором ссылки на диапазон – двоеточием (:).

Использование имен в качестве аргументов

В качестве аргументов функций могут использоваться имена, т.е. ссылки на ячейки и диапазоны. Выполняя вычисления, Excel просто использует текущее содержимое ячейки или диапазона. Функция СУММ возвращает сумму своих аргументов (или аргумента). Например, вычислить сумму значений диапазона А1:А20 можно с помощью такой формулы:

Если диапазон А1:А20 имеет имя (например, Продажи), то оно может быть использовано вместо ссылки на диапазон:

Использование столбцов и строк в качестве аргументов

Иногда в качестве аргумента функции удобно использовать строку или столбец полностью. К примеру, следующая формула возвращает сумму всех значений столбца В:

Ссылки на целую строку или столбец особенно эффективны в тех случаях, если диапазон, сумму значений которого следует вычислить, постоянно изменяется (например, если в таблицу периодически вносятся новые данные об объемах продаж). Прежде чем использовать ссылку на целую строку или столбец, убедитесь в том, что они не содержат данных, которые не должны быть включены в сумму.

Не следует беспокоиться о том, что суммирование такого громадного диапазона значений (столбец, например, состоит из 1048576 ячеек) может увеличить время вычисления. Дело в том, что Excel “помнит”, в каком столбце и в какой строке располагается последнее значение. Поэтому, вычисляя результат формулы с помощью ссылки на целую строку или столбец, программа не будет принимать в расчет ячейки, выходящие за пределы последнего использованного столбца и строки.

Использование литералов в качестве аргументов

Литерал – это числовое значение или текстовая строка, которые указаны непосредственно в выражении. Например, функция КОРЕНЬ, которая возвращает значение квадратного корня, имеет один аргумент. В следующем примере в качестве аргумента функции используется литерал:

В некоторых случаях использование литерального аргумента лишает формулу всякого смысла. Эта формула всегда возвращает одно и то же значение, поэтому ее можно просто заменить цифрой 15. Использовать такую формулу можно разве что в случае, когда вы хотите дать понять, что 15 – это квадратный корень из 225.

Использование литералов оправдано, если формула имеет два и более аргументов. Функция ЛЕВСИМВ, имеющая два аргумента, возвращает крайние левые символы текстовой строки, являющейся первым аргументом функции. Второй аргумент определяет количество возвращаемых символов. Если ячейка А1 содержит текст Бюджет, следующая формула возвращает первую букву, т.е. Б:

Использование выражений в качестве аргументов

Excel позволяет использовать в качестве аргументов выражения. Такие выражения следует рассматривать как формулы в формуле. Если в качестве аргумента используется выражение, Excel сначала вычисляет значение этого выражения, а затем использует его в качестве аргумента. Рассмотрим следующий пример:

В этой формуле используется функция КОРЕНЬ, единственным аргументом которой выступает следующее математическое выражение:

Вычисляя значение формулы, Excel сначала вычисляет значение выражения в аргументе функции, а затем извлекает квадратный корень из результата вычислений.

Использование других функций в качестве аргументов

Итак, в качестве аргументов функций могут выступать математические выражения. Очевидно, что эти выражения, в свою очередь, содержат другие функции. Функции, которые используются внутри других функций, называются вложенными. Прежде всего, Excel оценивает значение выражения с наибольшей глубиной вложения, а затем – все остальные. Рассмотрим следующий пример вложенной функции:

Функция РАДИАНЫ преобразует градусы в радианы – единицы измерения, которые используются во всех тригонометрических функциях Excel. Если в ячейке В9 задан угол в градусах, функция РАДИАНЫ преобразует градусы в радианы, а затем функция SIN вычисляет синус этого угла.

Формула может содержать не более 64 уровней вложенных функций. Вряд ли вы когда-либо напишете такое длинное выражение.

Использование массивов в качестве аргументов

В качестве аргумента функции может быть использован массив. Массив представляет собой ряд значений, разделенных точкой с запятой и заключенных в скобки. В приведенной ниже формуле используется функция ИЛИ, в качестве аргумента которой применен массив. Формула возвращает ИСТИНА, если ячейка А1 содержит значение 1, 3 или 5.

Очень часто использование массивов помогает упростить формулу. Например, следующая формула возвращает тот же результат, что и предыдущая, но в качестве аргумента в ней используется не массив, а функции ЕСЛИ. Как видите, формула с массивом намного проще.

Источник

Что такое функция?

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Функция. Аргумент. Прямая и обратная зависимость

Содержание

Вокруг нас происходит множество событий или процессов, которые можно измерить. При этом величина одних зависит от величины каких-либо других.

Так, например, от того, сколько мы испишем страниц в тетради, зависит количество оставшихся в стержне чернил. Чем больше кружек наполнено компотом, тем меньше его останется в кастрюле. Чем больше мама оставит денег на обеды, тем больше можно на них купить мороженого. А чем сильнее велосипедист крутит педали, тем больше километров он проедет. Придумайте свои примеры?

В наших описанных выше примерах первые два имеют обратную зависимость, то есть при увеличении одной величины (количество страниц и кружек в наших случаях), уменьшается вторая (количество чернил и компота в кастрюле).

Обратная зависимость

Примеры с велосипедистом и мороженым имеют прямую зависимость, то есть при увеличении одной величины (скорость движения педалями и количество оставленных мамой денег) увеличивается и другая (пройденное расстояние и количество мороженого).

Прямая пропорциональность

Зависимость, которая показывает как одна величина связана с другой величиной, как раз и называется функцией.

Аргумент и функция

Зависимые и независимые переменные могут обозначаться и любыми другими буквами (латинскими или греческими).

Примеры аргумента и функции

Запись функции

Слово «функция» произошло от латинского слова functio – исполнение, осуществление. Это одно из главных понятий в математике, показывающее зависимость одних переменных величин от других. Понятие «величина» в данном случае может включать в себя совершенно любое число.

Переменные могут принимать как положительные, так и отрицательные значения.

Источник