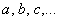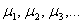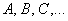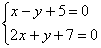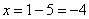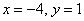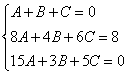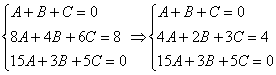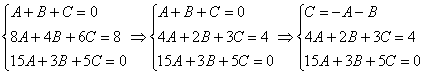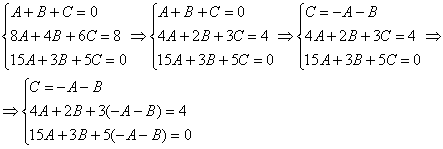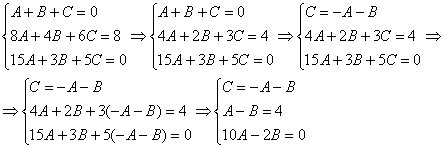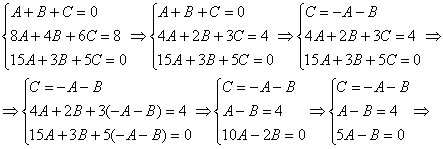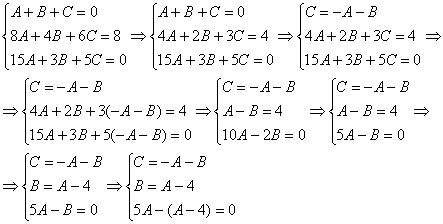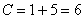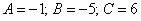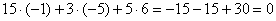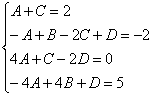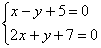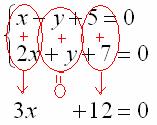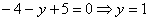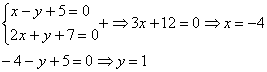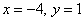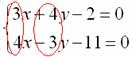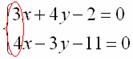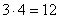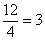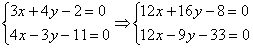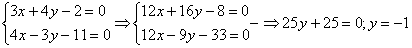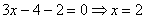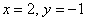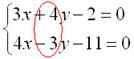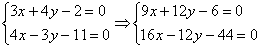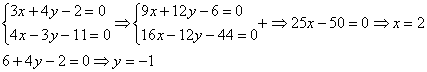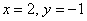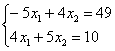Что можно делать с системами уравнений

Система уравнений

Пример системы уравнений

Существует два метода решений систем линейных уравнений:

Алгоритм решения системы уравнений методом подстановки:

Решить систему уравнений методом подстановки

Решение:

y = − 28 − 7 = 28 7 = 4

x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0

Ответ можно записать одним из трех способов:

Решение системы уравнений методом сложения.

Метод сложения основывается на следующем свойстве:

Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.

Решить систему уравнений методом сложения

Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.

( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )

− 3 x − 6 y + 3 x − y = − 24 − 4

y = − 28 − 7 = 28 7 = 4

Ответ можно записать одним из трех способов:

Задания для самостоятельного решения

№1. Решите систему уравнений < 4 x + y = 10 x + 3 y = − 3

В ответе запишите сумму решений.

Решение:

1 способ: (метод подстановки)

x + 3 ( 10 − 4 x ) = − 3

y = 10 − 4 x = 10 − 4 ⋅ 3 = − 2

В ответе надо указать сумму решений:

2 способ: (метод сложения)

( − 12 x − 3 y + ( x + 3 y ) = ( − 30 ) + ( − 3 )

− 12 x − 3 y + x + 3 y = − 30 − 3

В ответе надо указать сумму решений:

Решение:

y = − 20 − 5 = 20 5 = 4

x = 6 − 2 y = 6 − 2 ⋅ 4 = 6 − 8 = − 2

Запишите координаты в ответе через точку с запятой.

Решение:

Для того, чтобы найти точки пересечения графиков, необходимо составить систему уравнений. Будем решать эту систему методом подстановки:

D = b 2 − 4 a c = ( − 2 ) 2 − 4 ⋅ 1 ⋅ ( − 3 ) = 4 + 12 = 16

x 1,2 = − b ± D 2 a = − ( − 2 ) ± 16 2 ⋅ 1 = [ 2 + 4 2 = 6 2 = 3 2 − 4 2 = − 2 2 = − 1

Ищем координату y (ординату), соответствующую координате x = 3 (абсциссе).

Источник

Алгебра. Урок 4. Уравнения, системы уравнений

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Уравнения”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Линейные уравнения

Примеры линейных уравнений:

Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.

Примеры решения линейных уравнений:

Это линейное уравнение, так как переменная стоит в первое степени.

Попробуем преобразовать его к виду a x = b :

Для начала раскроем скобки:

− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5

Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.

Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:

Это уравнение не является линейным уравнением.

Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

Квадратные уравнения

Алгоритм решения квадратного уравнения:

Примеры решения квадратного уравнения:

D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64

D > 0 – будет два различных корня:

x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7

Ответ: x 1 = − 1, x 2 = 7

D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0

D = 0 – будет один корень:

x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2

D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31

Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо с = 0, либо b = с = 0 ). Смотрите видео, как решать такие квадратные уравнения!

Разложение квадратного трехчлена на множители

Квадратный трехчлен можно разложить на множители следующим образом:

a x 2 + b x + c = a ⋅ ( x − x 1 ) ⋅ ( x − x 2 )

где a – число, коэффициент перед старшим коэффициентом,

x – переменная (то есть буква),

a x 2 + b x + c = a ⋅ ( x − x 0 ) 2

Примеры разложения квадратного трехчлена на множители:

− x 2 + 6 x + 7 = ( − 1 ) ⋅ ( x − ( − 1 ) ) ( x − 7 ) = − ( x + 1 ) ( x − 7 ) = ( x + 1 ) ( 7 − x )

− x 2 + 4 x − 4 = ( − 1 ) ⋅ ( x − 2 ) 2 = − ( x − 2 ) 2

Если квадратный трехчлен является неполным, ( ( b = 0 или c = 0 ) то его можно разложить на множители следующими способами:

Дробно рациональные уравнения

Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает.

ОДЗ – область допустимых значений переменной.

В выражении вида f ( x ) g ( x ) = 0

ОДЗ: g ( x ) ≠ 0 (знаменатель дроби не может быть равен нулю).

Алгоритм решения дробно рационального уравнения:

Пример решения дробного рационального уравнения:

Решить дробно рациональное уравнение x 2 − 4 2 − x = 1.

Решение:

Будем действовать в соответствии с алгоритмом.

Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:

x 2 − 4 2 − x − 1 \ 2 − x = 0

x 2 − 4 2 − x − 2 − x 2 − x = 0

x 2 − 4 − ( 2 − x ) 2 − x = 0

x 2 − 4 − 2 + x 2 − x = 0

Первый шаг алгоритма выполнен успешно.

Обводим в рамочку ОДЗ, не забываем про него: x ≠ 2

x 2 + x − 6 = 0 – Квадратное уравнение. Решаем через дискриминант.

D = b 2 − 4 a c = 1 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 1 + 24 = 25

D > 0 – будет два различных корня.

x 1,2 = − b ± D 2 a = − 1 ± 25 2 ⋅ 1 = − 1 ± 5 2 = [ − 1 + 5 2 = 4 2 = 2 − 1 − 5 2 = − 6 2 = − 3

Корни, полученные на предыдущем шаге:

Значит, в ответ идет только один корень, x = − 3.

Системы уравнений

Пример системы уравнений

Существует два метода решений систем линейных уравнений:

Алгоритм решения системы уравнений методом подстановки:

Решить систему уравнений методом подстановки

Решение:

y = − 28 − 7 = 28 7 = 4

x = 8 − 2 y = 8 − 2 ⋅ 4 = 8 − 8 = 0

Ответ можно записать одним из трех способов:

Решение системы уравнений методом сложения.

Метод сложения основывается на следующем свойстве:

Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.

Решить систему уравнений методом сложения

Теперь, когда перед переменной в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.

( − 3 x − 6 y ) + ( 3 x − y ) = ( − 24 ) + ( − 4 )

− 3 x − 6 y + 3 x − y = − 24 − 4

y = − 28 − 7 = 28 7 = 4

Ответ можно записать одним из трех способов:

Задание №9 из ОГЭ 2020. Типовые задачи и принцип их решения.

Источник

Как решить систему линейных уравнений?

На данном уроке мы рассмотрим методы решения системы линейных уравнений. В курсе высшей математики системы линейных уравнений требуется решать как в виде отдельных заданий, например, «Решить систему по формулам Крамера», так и в ходе решения остальных задач. С системами линейных уравнений приходится иметь дело практически во всех разделах высшей математики.

Сначала немного теории. Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени: без всяких причудливых вещей вроде и т.п., от которых в восторге бывают только участники математических олимпиад.

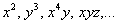
В высшей математике для обозначения переменных используются не только знакомые с детства буквы .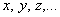
Довольно популярный вариант – переменные с индексами: .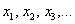
Либо начальные буквы латинского алфавита, маленькие и большие: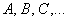
Не так уж редко можно встретить греческие буквы: 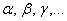– известные многим «альфа, бета, гамма». А также набор с индексами, скажем, с буквой «мю»:

Использование того или иного набора букв зависит от раздела высшей математики, в котором мы сталкиваемся с системой линейных уравнений. Так, например, в системах линейных уравнений, встречающихся при решении интегралов, дифференциальных уравнений традиционно принято использовать обозначения

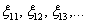
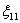
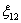
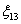
Но как бы ни обозначались переменные, принципы, методы и способы решения системы линейных уравнений от этого не меняются. Таким образом, если Вам встретится что-нибудь страшное типа , не спешите в страхе закрывать задачник, в конце концов, вместо можно нарисовать солнце, вместо – птичку, а вместо – рожицу (преподавателя). И, как ни смешно, систему линейных уравнений с данными обозначениями тоже можно решить.

Что-то у меня есть такое предчувствие, что статья получится довольно длинной, поэтому небольшое оглавление. Итак, последовательный «разбор полётов» будет таким::

– Решение системы линейных уравнений методом подстановки («школьный метод»);
– Решение системы методом почленного сложения (вычитания) уравнений системы;
– Решение системы по формулам Крамера;
– Решение системы с помощью обратной матрицы;
– Решение системы методом Гаусса.

С системами линейных уравнений все знакомы из школьного курса математики. По сути дела, начинаем с повторения.

Решение системы линейных уравнений методом подстановки

Данный метод также можно назвать «школьным методом» или методом исключения неизвестных. Образно говоря, его еще можно назвать «недоделанным методом Гаусса».

Решить систему линейных уравнений:

Здесь у нас дана система из двух уравнений с двумя неизвестными. Обратите внимание, что свободные члены (числа 5 и 7) расположены в левой части уравнения. Вообще говоря, без разницы, где они находятся, слева или справа, просто в задачах по высшей математике нередко они расположены именно так. И такая запись не должна приводить в замешательство, при необходимости систему всегда можно записать «как обычно»: 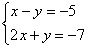. Не забываем, что при переносе слагаемого из части в часть у него нужно поменять знак.

Что значит решить систему линейных уравнений? Решить систему уравнений – это значит найти множество её решений. Решение системы представляет собой набор значений всех входящих в неё переменных, который обращает КАЖДОЕ уравнение системы в верное равенство. Кроме того, система может быть несовместной (не иметь решений). Не тушуйтесь, это общее определение =) У нас же будет всего лишь одно значение «икс» и одно значение «игрек», которые удовлетворяют каждому уравнению с-мы.

Существует графический метод решения системы, с которым можно ознакомиться на уроке Простейшие задачи с прямой. Там же я рассказал о геометрическом смысле системы двух линейных уравнений с двумя неизвестными. Но сейчас на дворе эра алгебры, и числа-числа, действия-действия.

Решаем: из первого уравнения выразим: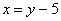
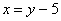
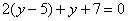
Полученное выражение подставляем во второе уравнение:

Раскрываем скобки, приводим подобные слагаемые и находим значение :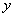

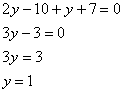
Далее вспоминаем про то, от чего плясали: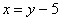
Значение 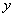нам уже известно, осталось найти:

Ответ:

После того, как решена ЛЮБАЯ система уравнений ЛЮБЫМ способом, настоятельно рекомендую выполнить проверку (устно, на черновике либо калькуляторе). Благо, делается это легко и быстро.

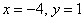
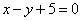
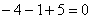
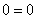
1) Подставляем найденный ответ в первое уравнение :

– получено верное равенство.

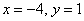
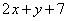
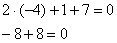
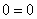
2) Подставляем найденный ответ во второе уравнение :

– получено верное равенство.

Или, если говорить проще, «всё сошлось»

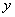
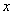
Рассмотренный способ решения не является единственным, из первого уравнения можно было выразить , а не .
Можно наоборот – что-нибудь выразить из второго уравнения и подставить в первое уравнение. Кстати, заметьте, самый невыгодный из четырех способов – выразить из второго уравнения: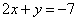

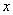
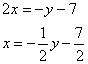
Получаются дроби, а оно зачем? Есть более рациональное решение.

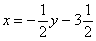
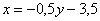
Тем не менее, в ряде случаев без дробей всё-таки не обойтись. В этой связи обращаю Ваше внимание на то, КАК я записал выражение. Не так: , и ни в коем случае не так: .

Если в высшей математике Вы имеете дело с дробными числами, то все вычисления старайтесь проводить в обыкновенных неправильных дробях.

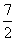
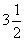
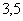
Именно , а не или !

Запятую можно использовать лишь иногда, в частности, если 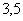– это окончательный ответ какой-нибудь задачи, и с этим числом больше не нужно выполнять никаких действий.

Многие читатели наверняка подумали «да зачем такое подробное объяснение, как для класса коррекции, и так всё понятно». Ничего подобного, вроде бы такой простой школьный пример, а сколько ОЧЕНЬ важных выводов! Вот еще один:

Любое задание следует стремиться выполнить самым рациональным способом. Хотя бы потому, что это экономит время и нервы, а также снижает вероятность допустить ошибку.

Если в задаче по высшей математике Вам встретилась система двух линейных уравнений с двумя неизвестными, то всегда можно использовать метод подстановки (если не указано, что систему нужно решить другим методом) Ни один преподаватель не подумает, что ты лох снизит оценку за использование «школьного метода».
Более того, в ряде случаев метод подстановки целесообразно использовать и при большем количестве переменных.

Решить систему линейных уравнений с тремя неизвестными

Похожая система уравнений часто возникает при использовании так называемого метода неопределенных коэффициентов, когда мы находим интеграл от дробно-рациональной функции. Рассматриваемая система взята мной как раз оттуда.

При нахождении интеграла – цель быстро найти значения коэффициентов 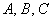, а не изощряться формулами Крамера, методом обратной матрицы и т.д. Поэтому, в данном случае уместен именно метод подстановки.

Когда дана любая система уравнений, в первую очередь желательно выяснить, а нельзя ли ее как-нибудь СРАЗУ упростить? Анализируя уравнения системы, замечаем, что второе уравнение системы можно разделить на 2, что мы и делаем:

Справка: математический знак 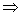обозначает «из этого следует это», он часто используется в ходе решения задач.

Теперь анализируем уравнения, нам нужно выразить какую-нибудь переменную через остальные. Какое уравнение выбрать? Наверное, Вы уже догадались, что проще всего для этой цели взять первое уравнение системы:

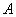
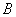
Здесь без разницы, какую переменную выражать, можно было с таким же успехом выразить или .

Далее, выражение для 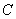подставляем во второе и третье уравнения системы:

Раскрываем скобки и приводим подобные слагаемые:

Третье уравнение делим на 2:

Из второго уравнения выразим 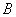и подставим в третьей уравнение:

Практически всё готово, из третьего уравнения находим: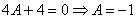
Из второго уравнения: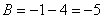
Из первого уравнения:

Ответ:

Проверка: Подставим найденные значения переменных в левую часть каждого уравнения системы:

1)
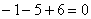
2)
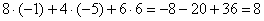
3)

Получены соответствующие правые части уравнений, таким образом, решение найдено верно.

Решить систему линейных уравнений с 4 неизвестными

Это пример для самостоятельного решения (ответ в конце урока).

Решение системы методом почленного сложения (вычитания) уравнений системы

В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, впрочем, сейчас станет всё понятнее.

Решить систему линейных уравнений:

Я взял ту же систему, что и первом примере.
Анализируя систему уравнений, замечаем, что коэффициенты при переменной 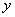одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно:

Действия, обведенные красным цветом, выполняются МЫСЛЕННО.
Как видите, в результате почленного сложения у нас пропала переменная 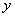. В этом, собственно, и состоит суть метода – избавиться от одной из переменных.

Теперь всё просто: 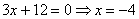– подставляем в первое уравнение системы (можно и во второе, но это не так выгодно – там числа больше):

В чистовом оформлении решение должно выглядеть примерно так:

Ответ:

У некоторых явно возник вопрос: «Зачем все эти изыски, если можно просто выразить одну переменную через другую и подставить во второе уравнение?».

Решить систему линейных уравнений: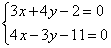

В данном примере можно использовать «школьный» метод, но большой минус состоит в том, что когда мы будем выражать какую-либо переменную из любого уравнения, то получим решение в обыкновенных дробях. А возня с дробями займет время, к тому же, если у Вас не «набита рука» на действиях с дробями, то велика вероятность допустить ошибку.

Поэтому целесообразно использовать почленное сложение (вычитание) уравнений. Анализируем коэффициенты при соответствующих переменных:

Как видим числа в парах (3 и 4), (4 и –3) – разные, поэтому, если сложить (вычесть) уравнения прямо сейчас, то от переменной мы не избавимся. Таким образом, хотелось бы видеть в одной из пар одинаковые по модулю числа, например, 20 и 20 либо 20 и –20.

Будем рассматривать коэффициенты при переменной :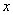

Подбираем такое число, которое делилось бы и на 3 и на 4, причем оно должно быть как можно меньше. В математике такое число называется наименьшим общим кратным. Если Вы затрудняетесь с подбором, то можно просто перемножить коэффициенты:

Далее:
Первое уравнение умножаем на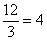
Второе уравнение умножаем на

В результате:

Вот теперь из первого уравнения почленно вычитаем второе. На всякий случай привожу еще раз действия, которые проводятся мысленно: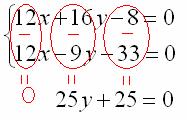

Следует отметить, что можно было бы наоборот – из второго уравнения вычесть первое, это ничего не меняет.

Теперь подставляем найденное значение 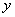в какое-нибудь из уравнений системы, например, в первое:

Ответ:

Решим систему другим способом. Рассмотрим коэффициенты при переменной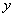

Очевидно, что вместо пары коэффициентов (4 и –3) нам нужно получить 12 и –12.
Для этого первое уравнение умножаем на 3, второе уравнение умножаем на 4:

Почленно складываем уравнения и находим значения переменных:

Ответ:

Второй способ несколько рациональнее, чем первый, так как складывать проще и приятнее чем вычитать.

В высшей математике всегда стремимся складывать и умножать, а не вычитать и делить.

Решить систему линейных уравнений:

Это пример для самостоятельного решения (ответ в конце урока).

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник