Что можно определить по диаграмме состояния

Определение диаграммы состояния

Сплавы называют однородными (гомогенными), если структура их однофазная, и разнородными (гетерогенны­ми), если структура их состоит из нескольких фаз. Для сплавов, образованных одними и теми же компонентами, фазовое состояние описывается диаграммой состояния.

Пользуясь диаграммой состояния, можно установить воз­можность проведения термической обработки и ее режимы, температуры литья, горячей пластической деформации и т. д.

Правило фаз

Правило фаз устанавливает температурные условия про­цесса кристаллизации при заданном давлении, а также опре­деляет, сколько фаз должно быть в чистом компоненте или в сплаве определенного состава, если они находятся в равно­весном состоянии при данной температуре (или давлении). Число факторов, которые можно менять, не изменяя фазово­го состава сплава, называется степенью свободы.

Правило фаз выражает зависимость между числом степе­ней свободы С (вариантностью) системы, числом компонен­тов К и числом фаз Ф системы, находящихся в равновесии (рис. 3)

Обычно все превращения в металлах и сплавах происхо­дят при постоянном давлении (атмосферном). Тогда правило фаз записывается так:

Уравнение правила фаз позволяет корректировать пра­вильность построения диаграмм состояния.

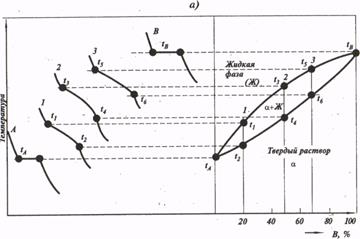
Рис. 3 Методы построения диаграмм состояния

В результате измерений получают серию кривых охлаж­дения, на которых при температурах фазовых превращений наблюдаются точки перегиба и температурные остановки.

Температуры, соответствующие фазовым превращениям, называются критическими точками.

Вид диаграммы состояния определяется характером взаи­модействий, которые возникают между компонентами в жид­ком и твердом состояниях. Во всех случаях предполагают, что в жидком состоянии существует неограниченная раство­римость, то есть однородная фаза существует при любом со­отношении компонентов.

Диаграммы с ограниченной растворимостью или с пол­ным отсутствием растворимости в жидком состоянии практи­ческого значения не имеют, так как сплавы этих систем мало применяются в технике.

Источник

Анализ диаграмм состояния

По диаграмме состояния можно определить критические точки сплава при нагревании и охлаждении и установить его структуру, выбрать сплав, обладающий наилучшими литейными свойствами, правильно назначить режим термической обработки.

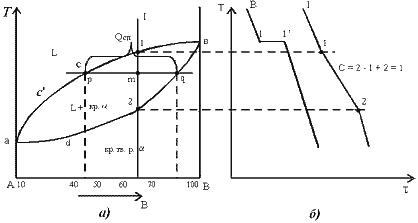
Диаграмма состояния сплавов, компоненты которой неограниченно растворимы в жидком состоянии, нерастворимы в твердом и при кристаллизации образуют эвтектику (рис. 3):

АЕС – ликвидус, начало кристаллизации сплавов.

ВЕF – солидус, конец кристаллизации сплавов; на этой линии происходит одновременная эвтектическая кристаллизация компонентов А и В при постоянной температуре. Линия называется эвтектической.

АЕ – начало кристаллизации компонента А.

ЕС – начало кристаллизации компонента В.

Точка Е называется эвтектической, в ней происходит одновре-
менная кристаллизация компонентов при самой низкой и постоянной
температуре.

Кристаллизация и структурообразование сплавов (I–III)

Сплав I – доэвтектический. Критическая точка 1 – начало кристаллизации компонента А, две фазы: жидкость и зародыши зерен компонента А.

Критическая точка 2 – кристаллизация эвтектики, т. е. из оставшейся к этой температуре жидкости одновременно кристаллизуютсякомпоненты А и В:

На кривой охлаждения образуется площадка 2-2. Структура сплавапосле охлаждения состоит из зерен компонента А и эвтектики.

По мере охлаждения сплава между точками I и 2 жидкость меняет свою концентрацию по линии AЕ. Чтобы определить состав твердой и жидкой фаз при заданной температуре t₁ сплава I (рис. 4), необходи­мо через точку t₁провести коноду, т. е. прямую линию, параллельную оси концентрации, до пересечения с линиями диаграммы и точки пересечения спроектировать на ось концентрации. Точка пересечения l c линией ликвидус покажет концентрацию компонентов А и В в жидкой фазе, точка S – в твердой (чистый компонент А).

Соотношение масс фаз при заданной температуре можно определить по правилу отрезков.

Правило отрезков. Массы фаз относятся между собой как обрат­ная пропорция отрезков коноды. Например, при температуре t₁ сплав I имеет 2 фазы: жидкую и твердую с количеством масс Q_Ж и Q_ТВ, соотношение фаз определится выражением (2), а количество жидкой и твердой фаз – соотношениями (3) и (4):

где Р – общая масса сплава.

Присутствуют 3 фазы: жидкость эвтектического состава, компо­ненты А и В. На кривой охлаждения образуется площадка 1-1.

Структура сплава после охлаждения состоит из эвтектики (смеси кристаллов компонентов А и В).

Сплав III – заэвтектический. Критическая точка 1 – начало крис­таллизации компонента В. Фазы две: жидкость, кристаллы компонента В. По мере охлаждения сплава жидкость меняет концентрацию по линии ликвидус ЕС. Например, при t₂ состав жидкости определится точ­кой n, спроектированной на ось концентраций, а состав твердой фазы – проекцией точки m.

Критическая точка 2 – кристаллизация эвтектики, т. е. из остав­шейся к этой температуре жидкости при постоянной температуре кристаллизуются оба компонента:

Структура сплава после охлаждения состоит из зерен компонента В и эвтектики.

Правило фаз Гиббса устанавливает зависимость между числами фаз системы, ее компонентов и степеней свободы:

где С – число степеней свободы, или вариантность системы;

К – число компонентов системы;

Ф – число фаз, находящихся в равновесии в данной критической точке.

Под числом степеней свободы понимается число независимых па­раметров системы, которые можно изменить, не изменяя равновесия, например, температуру без изменения числа фаз. Так как степень свободы не может быть меньше нуля и дробным числом, то

Следовательно, в двойной системе в равновесии может находиться не более трех фаз, в тройной – не более четырех и т. д.

Например, определим число степеней свободы у сплава I в 1-й критической точке (рис. 5):

С = К – Ф + 1, С = 2(А, В) – 2(А, Ж) + 1 = 1,

т. е. с изменением температуры между точками 1-2 число фаз не изме­няется, а происходит переход одной фазы (жидкости) в другую (ком­понент А). Во второй точке

С = К – Ф + 1, С = 2(А, В) – 3(А, В, Ж) + 1 = 0,

т. е. процесс кристаллизации эвтектики идет при постоянной темпера­туре, система нонвариантна. Изменение температуры ведет к измене­нию количества фаз.

Диаграмма состояния сплавов, компоненты которой растворимы
в жидком состоянии, нерастворимы в твердом и при кристаллизации
образуют устойчивое химическое соединение (рис. 5).

Диаграмма рассматривается как совокупность двух диаграмм состояния, где в роли компонента выступает химическое соединение:

I часть диаграммы – компоненты А и А_тВ_n;

II часть диаграммы – компоненты В и А_тВ_n.

Обе части диаграммы характеризуются неограниченной раствори­мостью в жидком состоянии. В твердом состоянии они нерастворимы, при кристал­лизации образуется эвтектическая смесь, состоящая из кристаллов компонента и химического соединения.

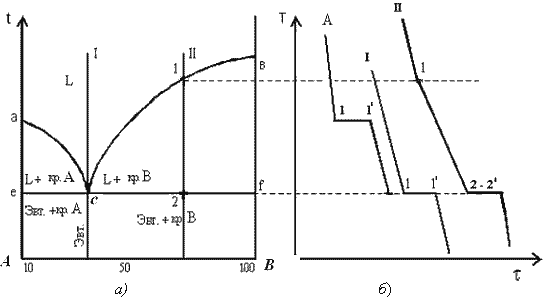
Диаграмма состояний сплавов, компоненты которой неограниченно растворимы друг в друге в жидком и твердом состояниях (рис. 6):

АnВ – ликвидус, начало кристаллизации твердого раствора;

АтВ – солидус, конец кристаллизации твердого раствора.

Кристаллизация и структурообразование сплавов (I)

Критическая точка 1 – начало кристаллизации твердого раство­ра α:

Критическая точка 2 – конец кристаллизации твердого раство­ра α.

При кристаллизации в интервале температур между точками 1-2 жидкая и твердая фазы изменяют состав. Изменение концентрации жид­кости определяется линией ликвидус АnВ, а концентрации твердого раствора – линией солидус АmВ. Например, в сплаве I при температу­ре t₁ состав жидкой фазы соответствует точке c, твердой – точ­ке d, спроектированными на ось концентраций. По правилу отрезков количество твердой фазы

Структура сплава: зерна однородного твердого раствора α.

Диаграмма состояния сплавов, компоненты которой неограничен­
но растворимы в жидком состоянии, ограниченно – в твердом, при
кристаллизации образуют эвтектическую смесь (эвтектику) (рис. 7).

АЕ – начало кристаллизации твердого раствора α;

АВ – конец кристаллизации твердого раствора α;

ЕС – начало кристаллизации твердого раствора β;

СF – конец кристаллизации твердого раствора β;

ВМ – ограничение растворимости компонента В в кристаллической решетке компонента А.

FN – ограничение растворимости компонента А в кристаллической решетке компонента В.

Точки В, F – максимальная растворимость компонентов друг в друге.

Диаграмма отличается от диаграммы (рис. 3) наличием двух об­ластей граничных твердых растворов α и β. Компоненты в чистом виде в сплавах этой системы макроскопически не присутствуют, а находятся только в виде твердых растворов α и β.

Кристаллизация и структурообразование в сплавах, состав которых находится в интервале проекций точек В и F диаграммы (рис. 7) на ось концентраций, происходят аналогично ранее рассмотренным примерам диаграммы с нерастворимыми в твердом состоянии компонентами, только вместо компонентов А и В присутствуют твердые растворы αи β.

Кристаллизация и структурообразование сплавов IV (V)

Критическая точка 1 – начало кристаллизации твердого раствора.α(β), две фазы: жидкость и α(β). В интервале темпера­тур между точками 1 и 2 идет кристаллизация:

Критическая точка 2 – конец кристаллизации α(β), в структуре сплава осталась одна фаза – α(β). В интервале температур меж­ду точками 2 и 3 – охлаждение твердого раствора α(β). За счет снижения растворимости твердый раствор становится насыщенным. Критическая точка 3 – начало выделения вторичного твердого раство­ра β_II(α_II) из пересыщенного твердого раствора α(β) вследствие уменьшения растворимости компонентов при снижении температу­ры. В интервале температур между точкой 3 и комнатной выделяется вторичный твердый раствор β_II(α_II). В структуре сплава две фазы:

Источник

Тема: «Изучение диаграмм состояния»

Цель работы: ознакомление студентов с основными видами диаграмм состояния, их основными линиями, точками, их значением.

Ход работы:

1.Изучите теоретическую часть.

2.Выполните задания практической части.

Теоретическая часть

Диаграмма состояния представляет собой графическое изображение состояния любого сплава изучаемой системы в зависимости от концентрации и температуры (см.рис. 1)

Рис.1 Диаграмма состояния

Диаграммы состояния показывают устойчивые состояния, т.е. состояния, которые при данных условиях обладают минимумом свободной энергии, и поэтому ее также называют диаграммой равновесия, так как она показывает, какие при данных условиях существуют равновесные фазы.

Построение диаграмм состояния наиболее часто осуществляется при помощи термического анализа. В результате получают серию кривых охлаждения, на которых при температурах фазовых превращений наблюдаются точки перегиба и температурные остановки.

По диаграмме состояния можно определить температуры фазовых превращений, изменение фазового состава, приблизительно, свойства сплава, виды обработки, которые можно применять для сплава.

Ниже представлены различные типы диаграмм состояния:

Рис.2. Диаграмма состояния сплавов с неограниченной растворимостью

компонентов в твердом состоянии (а); кривые охлаждения типичных

Анализ полученной диаграммы (рис.2).

1. Количество компонентов: К = 2 (компоненты А и В).

2. Число фаз: f = 2 (жидкая фаза L, кристаллы твердого раствора )

3. Основные линии диаграммы:

· acb – линия ликвидус, выше этой линии сплавы находятся в жидком состоянии;

· adb – линия солидус, ниже этой линии сплавы находятся в твердом состоянии.

Рис.3. Диаграмма состояния сплавов с отсутствием растворимости компонентов в твердом состоянии (а) и кривые охлаждения сплавов (б)

Анализ диаграммы состояния (рис. 3).

1. Количество компонентов: К = 2 (компоненты А и В);

2. Число фаз: f = 3 (кристаллы компонента А, кристаллы компонента В, жидкая фаза).

3. Основные линии диаграммы:

· линия ликвидус acb, состоит из двух ветвей, сходящихся в одной точке;

· линия солидус ecf, параллельна оси концентраций стремится к осям компонентов, но не достигает их;

Рис. 4. Диаграмма состояния сплавов с ограниченной растворимостью компонентов в твердом состоянии (а) и кривые охлаждения типичных сплавов (б)

Анализ диаграммы состояния (рис. 4).

1. Количество компонентов: К = 2 (компоненты А и В);

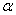
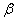
2. Число фаз: f = 3 (жидкая фаза и кристаллы твердых растворов (раствор компонента В в компоненте А) и ( раствор компонента А в компоненте В));

3. Основные линии диаграммы:

· линия ликвидус acb, состоит из двух ветвей, сходящихся в одной точке;

· линия солидус аdcfb, состоит из трех участков;

· dm – линия предельной концентрации компонента В в компоненте А;

· fn – линия предельной концентрации компонента А в компоненте В.

Практическая часть

Задание для студентов:

1. Запишите название работы и ее цель.

2. Запишите что такое диаграмма состояния.

Ответьте на вопросы:

1. Как строится диаграмма состояния?

2. Что можно определить по диаграмме состояния?

3. Какие названия имеют основные точки диаграммы?

4. Что указывается на диаграмме по оси абсцисс? Оси ординат?

5. Как называются основные линии диаграммы?

Задание по вариантам:

Студенты отвечают на одни и те же вопросы, различными являются рисунки, по которым необходимо отвечать. 1 вариант дает ответы по рисунку 2, 2 вариант дает ответы по рисунку 3, вариант 3 дает ответы по рисунку 4. Рисунок необходимо зафиксировать в тетрадь.

1. Как называется диаграмма?

2. Назовите сколько компонентов участвуют в образовании сплава?

3. Какими буквами обозначены основные линии диаграммы?

Практическая работа № 3

Тема: «Изучение чугунов»

Цель работы: ознакомление студентов с маркировкой и областью применения чугунов; формирование умения расшифровки марок чугунов.

Ход работы:

1.Ознакомьтесь с теоретической частью.

2.Выполните задание практической части.

Теоретическая часть

В зависимости от состояния углерода в чугуне различают: белый чугун – углерод в связанном состоянии в виде цементита, в изломе имеет белый цвет и металлический блеск; серый чугун – весь углерод или большая часть находится в свободном состоянии в виде графита, а в связанном состоянии находится не более 0,8 % углерода. Из-за большого количества графита его излом имеет серый цвет; половинчатый – часть углерода находится в свободном состоянии в форме графита, но не менее 2 % углерода находится в форме цементита. Мало используется в технике.

Графитовые включения можно рассматривать как соответствующей формы пустоты в структуре чугуна. Около таких дефектов при нагружении концентрируются напряжения, значение которых тем больше, чем острее дефект. Отсюда следует, что графитовые включения пластинчатой формы в максимальной мере разупрочняют металл. Более благоприятна хлопьевидная форма, а оптимальной является шаровидная форма графита. Пластичность зависит от формы таким же образом. Наличие графита наиболее резко снижает сопротивление при жестких способах нагружения: удар; разрыв. Сопротивление сжатию снижается мало.

Серые чугуны

Серый чугун широко применяется в машиностроении, так как легко обрабатывается и обладает хорошими свойствами. В зависимости от прочности серый чугун подразделяют на 10 марок (ГОСТ 1412).

Серые чугуны при малом сопротивлении растяжению имеют достаточно высокое сопротивление сжатию. Структура металлической основы зависит от количества углерода и кремния.

Например: СЧ 10 – серый чугун, предел прочности при растяжении 100 Мпа.

Ковкий чугун

Хорошие свойства у отливок обеспечиваются, если в процессе кристаллизации и охлаждения отливок в форме не происходит процесс графитизации. Чтобы предотвратить графитизацию, чугуны должны иметь пониженное содержание углерода и кремния.

По механическим и технологическим свойствам ковкий чугун занимает промежуточное положение между серым чугуном и сталью. Недостатком ковкого чугуна по сравнению с высокопрочным является ограничение толщины стенок для отливки и необходимость отжига.

Отливки из ковкого чугуна применяют для деталей, работающих при ударных и вибрационных нагрузках.

Из ферритных чугунов изготавливают картеры редукторов, ступицы, крюки, скобы, хомутики, муфты, фланцы.

Из перлитных чугунов, характеризующихся высокой прочностью, достаточной пластичностью, изготавливают вилки карданных валов, звенья и ролики цепей конвейера, тормозные колодки.

Например: КЧ 30-6 – ковкий чугун, предел прочности при растяжении 300Мпа, относительное удлинение 6 %.

Высокопрочный чугун

Получают эти чугуны из серых, в результате модифицирования магнием или церием. По сравнению с серыми чугунами, механические свойства повышаются, это вызвано отсутствием неравномерности в распределении напряжений из-за шаровидной формы графита.

Отливки коленчатых валов массой до 2..3 т, взамен кованых валов из стали, обладают более высокой циклической вязкостью, малочувствительны к внешним концентраторам напряжения, обладают лучшими антифрикционными свойствами и значительно дешевле.

Например: ВЧ 50 – высокопрочный чугун с пределом прочности на растяжение 500 Мпа.

Источник

диаграмма состояния

Д. с. однокомпонентного вещества обычно строится на плоскости в координатах T-P, T-V, P-V, T-H и др. Темп-pa равновесия двух фаз однокомпонентного вещества при заданном давлении определяется точкой пересечения кривых G(T)этих фаз (рис. 1). В тройных точках пересекаются три кривые попарного равновесия фаз, эти точки соответствуют равновесию трёх фаз. Равновесие большего числа фаз невозможно. Кривая равновесия двух фаз может оканчиваться в критической точке.

Для двухкомпонентных веществ система ур-ний (*) геометрически соответствует условиям общего касания к кривым G(с) (рис. 2) сосуществующих фаз; точки касания определяют структуру и составы фаз, находящихся в равновесии при заданных условиях. Концентрации фаз в двухфазном состоянии определяют с помощью конод (изотермич. прямых на изобарич. сечениях, соединяющих точки фазовых границ; см. рис. 3, а). Относит. количества фаз в двухфазном состоянии определяются правилом рычага.

Рис. 1. Зависимость энергии Гиббса G двух фаз I и II от температуры.

Рис. 2. Участки диаграммы состояния разных типов (вверху) и соответствующие им кривые G(с).

При фазовых переходах 2-го рода правило фаз Гиббса неприменимо, поэтому на T-с Д. с. такие фазы не всегда разделяются двухфазными областями, в отличие от переходов 1-го года (см. рис. 2,в, выше K₂).

Д. с. могут иметь разнообразную форму (рис. 3). К одному типу могут быть отнесены Д. с., на к-рых сохраняются неизменными число, размерность и взаимное расположение всех геом. элементов (характерных точек, линий, областей). Форма и размер отрезков линий и областей могут изменяться при сохранении типа Д. с. К характерным точкам относятся: критич. точки, точки фазовых переходов 2-го рода, трикритич. точки, точки равных концентраций с максимумом или минимумом M (рис. 3, б, в, е), точки равновесия трёх фаз (тройные точки на Д. с. однокомпонентного вещества), эвтектическая E (рис. 3, г), перитектическая P (рис. 3 д, и), монотектическая (рис. 3, и)точки, точка инконгруэнтного плавления соединения J (рис. 3, з). К характерным точкам можно также отнести точки фазовых переходов компонентов и соединений (в последнем случае при наличии сингулярной точки Д. с. разбивается на две: см. рис. 3, ж), точки максимумов и минимумов на их кривых плавления. На одной Д. с. может быть неск. характерных точек. Появление или исчезновение одной из них меняет тип Д. с. Эволюция T-с изобарич. сечений Т-Р-с Д. с. при изменении давления может привести к смене типов этих сечений (рис. 4) при переходе через граничные (переходные) Д. с. (рис. 4, б, д).

Д. с. трёхкомпонентного вещества при пост. P трёхмерна. Система координат, в к-рой она изображается, представляет собой рёбра трёхгранной призмы, основанием к-рой служит концентрац. треугольник; ось T перпендикулярна основанию, а грани являются Д. с. бинарных систем.

Рис. 5. Изотермическое сечение диаграммы состояний трёхкомпонентного вещества в случае ограниченной растворимости в твёрдых растворах и

Имеется ряд ограничений на структуру Д. с. Так, согласно третьему началу термодинамики, при T=0 К энтропия S=0, откуда вытекает неустойчивость растворов при К, они должны расслаиваться на смеси компонентов, соединений и стехиометрически упорядоченных фаз. Однако из-за малой диффузионной подвижности при К в большинстве случаев полного расслоения растворов наблюдать не удаётся. Границы равновесия двух фаз могут сливаться только в точках превращений чистых компонентов или в точках минимума или максимума этих границ.

Д. с., как правило, являются сложными и могут быть расчленены на простейшие. Д. с. на рис. 4, а-в являются простейшими. Д. с. на рис. 4, г—е расчленяются на три простейшие: , к-рые полностью или частично метастабильны. Д. с. одного и того же типа может быть как простейшей, так и сложной (ср. рис. 4, в, е). На Д. с. рис. 4, а—в можно нанести только одну линию T₀(с)изоконцентрац. равновесия, ; на Д. с. рис. 4, г-е три такие линии: , . При изменении давления (или смене одного из компонентов) простейшие Д. с., составляющие сложную, смещаются относительно друг друга, что приводит к стабилизации одних участков Д. с. и дестабилизации других. Тип простейших Д. с. определяется термодинамич. свойствами компонентов в сосуществующих фазах и термодинамич. свойствами растворов.

Для построения Д. с. используют данные разл. методов: рентгеноструктурного, калориметрического, термического, дилатометрического, оптич. и электронной микроскопии, ЯМP и др.

Д. с. можно рассчитать, если известны аналитич. выражения для G(T,P,с)всех фаз, образующихся в данной системе. Для определения вида G(T, P, с)достаточно иметь эксперим. данные о термодинамич. свойствах системы. Однако обычно такие данные либо отсутствуют, либо неполны. Для конструирования G(T, P, с)используют поэтому теорию растворов, электронную теорию вещества, разл. рода эмпирич. и полуэмпирич. соотношения. Привлекают закономерности изменения свойств элементов с изменением их атомного номера и положения в таблице Менделеева, а также имеющиеся данные об известных участках Д. с., метастабильных фазах в рассматриваемой системе, её физ. свойствах. Наиб. перспективным путём построения Д. с. является оптим. сочетание всех методов (эксперим. и теоретич.) нахождения ф-ций G(T, P, с) и последующего расчёта с помощью ЭВМ.

Д. с. используют на практике в материаловедении, металлургии, металловедении, химии, геологии и др.

Лит.: Ландау Л. Д., Лифшиц E. M., Статистическая физика, 3 изд., ч. 1, M., 1976; Древинг В. П., Калашников Я. А., Правило фаз с изложением основ термодинамики, 2 изд., M., 1964; Захаров A. M., Диаграммы состояния двойных и тройных систем, 2 изд., M., 1978; Устойчивость фаз в металлах и сплавах, пер. с англ., M., 1970; Кауфман Л., Бернстейн Г., Расчёт диаграмм состояния с помощью ЭВМ, пер. с англ., M., 1972; Гиббс Дж. В., Термодинамика. Статистическая механика, пер. с англ., M., 1982; Аптекарь И. Л., Исаева Л. Г., Анализ возможных типов диаграмм состояния двухкомпонентных систем и эволюция под давлением, в сб.: Физика и техника высоких давлений, в. 12, К., 1983.

И. Л. Аптекарь, Д. С. Каменецкая.

Источник