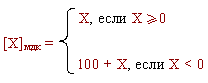что такое модифицированные обратный и дополнительный коды
Модифицированные обратный и дополнительный коды



При переполнении разрядной сетки, происходит перенос единицы в знаковый разряд. Это приводит к неправильному результату, причем положительное число, получившееся в результате арифметической операции может восприниматься как отрицательное (так как в знаковом разряде «1») и наоборот.
Здесь X и Y – коды положительных чисел, но ЭВМ воспринимает результат их сложения как код отрицательного числа (“1” в знаковом разряде). Для обнаружения переполнения разрядной сетки вводятся модифицированные коды.
Модифицированный обратный код – в нем под знак числа отводится не один, а два разряда. Форма записи чисел в модифицированном обратном коде выглядит следующим образом:
1) для положительного числа
X= 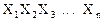
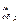
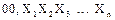
2) для отрицательного числа
X= 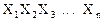
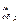
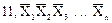
В модифицированном обратном и модифицированном дополнительном кодах под знак числа отводится не один, а два разряда: «00» соответствует знаку «+», «11» – знаку «-«. Любая другая комбинация (“01” или “10”), получившаяся в знаковых разрядах служит признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем не отличается от сложения в обычных обратном и дополнительном кодах.
Рассмотрим предыдущий пример, выполнив сложение в модифицированном обратном коде:
| X= 00,101011 Y= 00,110100 X+Y= 01,011111 |
В ЭВМ в процессе работы оба знаковых разряда сравниваются. В случае появления признака переполнения машина останавливается.
Модифицированный дополнительный код также рассматривает два знаковых разряда, а во всем остальном ничем не отличается от обычного дополнительного кода, то есть:
1) для положительного числа
X= 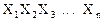
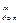
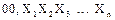
2) для отрицательного числа
Пример. Даны два числа: X=101001 и Y= –11010. Сложить их в дополнительном и модифицированном дополнительном кодах.
1) Переведем X и Y в дополнительный и модифицированный дополнительный код:
| Обычная запись | Обратный код | Дополнительный код |
| X=+0101001 Y=–0011010 | Xобр=0,0101001 Yобр=1,1100101 | Xдоп=0,0101001 Yдоп=1,1100110 |
| Обычная запись | Мод. обратный код | Мод. дополнительный код |
| X=+101001 Y=–011010 | 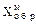 =00,101001 =00,101001 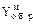 =11,100101 =11,100101 | 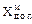 =00,101001 =00,101001 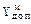 =11,100110 =11,100110 |
2) Выполним сложение:
  Xдоп= 0,0101001 Yдоп= 1,1100110 1)0,0001111 отбрасывается (X+Y)доп= 0,0001111 Xдоп= 0,0101001 Yдоп= 1,1100110 1)0,0001111 отбрасывается (X+Y)доп= 0,0001111 | X 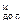 = 00,101001 Y = 00,101001 Y 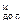 = 11,100110 1) 00,001111 отбрасывается (X+Y) = 11,100110 1) 00,001111 отбрасывается (X+Y) 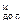 = 00,001111 = 00,001111 |
Переполнения нет (в знаковых разрядах “00”), поэтому результаты, полученные в обычном и модифицированном кодах совпадают (X+Y=1111).
Модифицированные коды
Важная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы.
При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым.
Рассмотрим такой пример:
То есть получаем неправильный результат как по знаку, так и в цифровой части.
Рассмотрим ещё один пример:
Можно заметить, что переполнение числовой сетки происходит в случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата.
Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата.
Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата.
Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд:
» + » ставится в соответствие 00
» – » ставится в соответствие 11
Тогда, по определению модифицированным дополнительным кодом числа называется
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
искажает младший знаковый разряд.
При этом различают два типа переполнения :
Модифицированные коды
Важная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы.
При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым.
Рассмотрим такой пример:
То есть получаем неправильный результат как по знаку, так и в цифровой части.
Рассмотрим ещё один пример:
Можно заметить, что переполнение числовой сетки происходит в случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата.
Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата.
Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата.
Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд:
» + » ставится в соответствие 00
» – » ставится в соответствие 11
Тогда, по определению модифицированным дополнительным кодом числа называется
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
искажает младший знаковый разряд.
При этом различают два типа переполнения :
Модифицированные коды
Важная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы.
При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым.
Рассмотрим такой пример:
То есть получаем неправильный результат как по знаку, так и в цифровой части.
Рассмотрим ещё один пример:
Можно заметить, что переполнение числовой сетки происходит в случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата.
Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата.
Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата.
Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд:
» + » ставится в соответствие 00
» – » ставится в соответствие 11
Тогда, по определению модифицированным дополнительным кодом числа называется
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
искажает младший знаковый разряд.
При этом различают два типа переполнения :
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода