Что такое пункт в алгебре
Что такое пункт в алгебре
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: 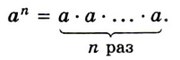
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
а m • а n = а m+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
(а m ) n = а mn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab) n = а n b n
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b) 2 = а 2 + 2аb + b 2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b) 2 = а 2 – 2аb + b 2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а 2 – b 2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а 3 + b 3 = (а + b)(a 2 – аb + b 2 )
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а 3 – b 3 = (а – b)(a 2 + ab + b 2 )
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :
Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Алгебра 7 класс Все формулы
Уравнения
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы 
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
Алгебра 7 класс Все формулы
Функции
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Значение слова «алгебра»
[Лат. algebra из араб.]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
А’ЛГЕБРА, ы, мн. нет, ж. [от араб.]. Отдел математики, часть математического анализа (см. анализ).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
а́лгебра
1. раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающих обычные операции сложения и умножения чисел
2. то же, что элементарная алгебра, раздел алгебры [1], охватывающий свойства операций с вещественными и комплексными числами, а также правила тождественных преобразований математических выражений и уравнений с использованием символов, обозначающих такие числа, и элементарных функций
3. тип алгебраических структур; множество из каких-либо объектов, над элементами которого определены некоторые операции, являющиеся, как правило, обобщением сложения и умножения
4. книжн. сложная система навыков, знаний, методов в какой-либо области ◆ Нужны объективные методы оценки эффективности производств, включающие в себя не только арифметику, но и социальную алгебру нашей действительности. Марина Наумова, «Рыба ищет где глубже», 2001 г. ◆ Очень грубый подсчёт показывает абсолютное преобладание тех, кто может выиграть от дерегулирования занятости. Почему тогда реформы в этой сфере остаются столь сложными с политической точки зрения? Почему аргумент от простой арифметики в их поддержку недостаточен, а необходима хитроумная алгебра политических комбинаций? Владимир Гимпельсон, «Пора дерегулировать?», 2003 г.
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: подгадать — это что-то нейтральное, положительное или отрицательное?
А́ЛГЕБРА
Том 1. Москва, 2005, стр. 415
Скопировать библиографическую ссылку:
А́ЛГЕБРА [ср.-век. лат. algebra, от араб. аль-джебр, аль-джабр – воссоединение (отдельных частей уравнения)], раздел математики, принадлежащий, наряду с арифметикой и геометрией, к числу старейших ветвей этой науки; она изучает операции над математич. объектами и влияет на формирование общих понятий и методов математики. Задачи и методы А. заключались первоначально в составлении и решении уравнений. В связи с исследованиями уравнений развивалось понятие числа, были введены отрицательные, рациональные, иррациональные и комплексные числа; общее исследование свойств этих числовых систем относится к А. В алгебре сформировались буквенные обозначения, позволившие записать свойства действий над числами в форме, не содержащей конкретных чисел. Преобразования по определённым правилам (связанным со свойствами действий) буквенных выражений составляет аппарат классич. А. Развитие А. оказало большое влияние на развитие новых областей математики, в частности математич. анализа, дифференциального и интегрального исчисления. Применение А. возможно всюду, где приходится иметь дело с операциями, аналогичными сложению и умножению чисел. Эти операции могут производиться над объектами самой различной природы. Наиболее известным примером такого расширенного применения алгебраич. методов является векторная алгебра (см. Линейная алгебра ) и её дальнейшее обобщение – тензорная алгебра (см. Тензорное исчисление ), ставшая одним из важных средств совр. физики.
Область определения функции
Прежде чем перейти к изучению области определения функции внимательно изучите уроки
«Что такое функция в математике» и «Как решать задачи на функцию».
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
Вместо « x » (аргумента функции) в формулу « у = 2x » подставляем произвольные числовые значения и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу « у = 2x » и запишем результаты в таблицу.
| x | y = 2 x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
| y = 2 ·
=
= 1 | ||||||
| x = 3 | y = 2 · 3 = 6 |
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
Вернемся к нашей функции « у = 2x » и найдем её область определения.
Посмотрим ещё раз на таблицу функции « y = 2x », где мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
| 1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать, что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
В нашей функции « у = 2x » вместо « x » можно подставить любое число, поэтому область определения функции « у = 2x » — это любые действительные числа.
Запишем область определения функции « у = 2x » через математические обозначения.
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на математические символы. Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции « у = 2x ». Так как в функции
« у = 2x » нет ограничений для « x », заштрихуем всю числовую ось от минус бесконечности « −∞ » до плюс бесконечности « +∞ ».
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как « x ∈ R ».
Читается « x ∈ R » как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
« x ∈ R » одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
№ 233 (2) Мерзляк 8 класс
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x » в функции
« f(x) =
| 8 |
| x + 5 |
».
По законам математики из школьного курса мы помним, что на ноль делить нельзя. Иначе говоря, знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции « f(x) =
| 8 |
| x + 5 |
». Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
Получается, что « x » может принимать любые числовые значения кроме « −5 ». На числовой оси заштрихуем все доступные значения для « x ».
Число « −5 » отмечено «пустой» точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число « −5 » не входит в область определения функции, при записи ответа рядом с ним будет стоять круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке «Как записать ответ неравенства».
Запишем окончательный ответ для области определения функции
« f(x) =
| 8 |
| x + 5 |
».
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
№ 98 (5) Колягин (Алимов) 8 класс
Найти область определения функции:
Из урока «Квадратный корень» мы помним, что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
« у = √ 6 − x ». Подкоренное выражение
« 6 − x » должно быть больше или равно нулю.
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
Запишем полученный ответ, используя числовую ось и математические символы. Число « 6 » отмечено «заполненной» точкой на числовой оси, так как входит в область допустимых значений.
Правило для определения области определения функции
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
№ 242 (3) Мерзляк 8 класс
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции « f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
» есть дробь «
| 1 |
| x 2 − 9 |
», где « x » расположен в знаменателе. Запишем условие, что знаменатель « x 2 − 9 » не может быть равен нулю.
Решаем квадратное уравнение через формулу квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −0 ± √ 0 2 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
| −0 ± √ 0 − (−36) |
| 2 |
Запомним полученный результат. Задаем себе второй вопрос. Проверяем, есть ли в формуле функции
« f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
» корень четной степени. В формуле есть квадратный корень « √ x + 3 ». Подкоренное выражение « x + 3 » должно быть больше или равно нулю.
Решим линейное неравенство.
Объединим полученные ответы по обоим вопросам:
Объединим все полученные результаты на числовых осях. Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях. Обратим внимание, что числа « −3 » и « 3 » отмечены «пустыми» точками и не входят в итоговое решение.

промежутка « −3 » и « x > 3 », которые являются областью определения функции
« f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
». Запишем окончательный ответ.
Примеры определения области определения функции
№ 101 Колягин (Алимов) 8 класс
Найти область определения функции:
Для поиска области определения функций задаем себе первый вопрос. Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
« y = 6 √ x + 5 √ 1 + x » нет дробей.
Задаем второй вопрос. Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени: « 6 √ x ». Степень корня — число « 6 ». Число « 6 » — чётное, поэтому подкоренное выражение корня « 6 √ x » должно быть больше или равно нулю.
В формуле функции « y = 6 √ x + 5 √ 1 + x » также есть корень пятой степени
« 5 √ 1 + x ». Степень корня « 5 » — нечётное число, значит, никаких ограничений на подкоренное выражение « 1 + x » не накладывается.
Получается, что единственное ограничение области определения функции
« y = 6 √ x + 5 √ 1 + x » — это ограничение подкоренного выражения « 6 √ x ».
Нарисуем область определения функции на числовой оси и запишем ответ.
№ 242 (4) Мерзляк 8 класс
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два. Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √ x + 2 ≠ 0 |
| x 2 − 7x + 6 ≠ 0 |
Обозначим их номерами « 1 » и « 2 » и решим каждое уравнение отдельно.
| √ x + 2 ≠ 0 (1) |
| x 2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
Если значение квадратного корня
« √ x + 2 ≠ 0 » не должно быть равно нулю, значит, подкоренное выражение
« x + 2 ≠ 0 » также не должно быть равно нулю.
Теперь решим уравнение под номером « 2 », используя формулу квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −(−7) ± √ (−7) 2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
| 7 ± √ 49 − 24 |
| 2 |
x1;2 =
| 7 ± 5 |
| 2 |
x1 ≠
| x2 ≠
|
x1 ≠
| x2 ≠
|
| x1 ≠ 6 | x2 ≠ 1 |
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
| x ≠ −2 |
| x ≠ 1 |
| x ≠ 6 |
В формуле функции
« f(x) =
| √ x − 4 |
| √ x + 2 |
+
| 4x − 3 |
| x 2 − 7x + 6 |
»
есть два корня « √ x − 4 » и « √ x + 2 ». Их подкоренные выражения должны быть больше или равны нулю.
| x − 4 ≥ 0 |
| x + 2 ≥ 0 |
| x − 4 ≥ 0 |
| x + 2 ≥ 0 |
| x ≥ 4 |
| x ≥ −2 |
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
Объединим в таблицу ниже полученные ответы по обеим проверкам:
Результат проверки, что знаменатели дробей с « x » не равны нулю
Результат проверки, что подкоренные выражения должно быть больше или равны нулю
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет всем полученным условиям.















