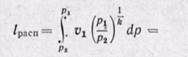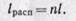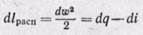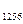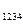Что такое работа расширения вытеснения располагаемая
Располагаемая работа
При истечении газа
Величина 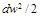
Из сравнения уравнений (4.8) и (10.6) следует, что для обратимого процесса течения газа
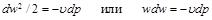
Равенство (10.10) показывает, что при движении рабочего тела по каналу знаки 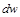
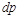
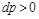
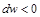
Если 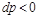
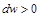
Эта закономерность лежит в основе специальных каналов переменного сечения, называемых соплами и диффузорами.
Если при перемещении газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом.
Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называется диффузором.
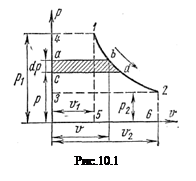
Располагаемую работу при истечении газа можно представить графически на 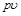
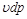
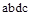
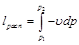
Приращение кинетической энергии потока газа (располагаемая работа), как это следует из (4.8) и (10.6) представляет собой разность работ расширения потока газа 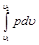
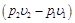
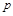
Если кривая 1–2 является политропой, то располагаемую работу определяем из уравнения
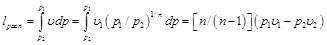
При адиабатном расширении идеального газа
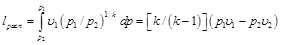
Сравнивая располагаемую работу при истечении (пл. 1234) с работой расширения газа (пл.1265), получаем, что величина располагаемой работы в n раз больше работы расширения газа:
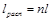
Из уравнения (10.4) следует, что
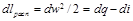
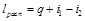
Располагаемая работа при течении газа может быть получена за счет внешней теплоты и уменьшения энтальпии газа. Это уравнение справедливо как для обратимых, так и для необратимых процессов течения газа с трением.
При адиабатном течении из уравнения (10.14)
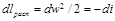
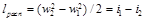
Из уравнения (10-15), принимая w1≈0 найдём скорость истечения
Дата добавления: 2020-07-18 ; просмотров: 227 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Располагаемая работа при истечении газа
Величинаравная бесконечно малому приращению внешней
кинетической 
Из сравнения уравнений (5-12) и (13-3) следует, что для обратимого процесса течения газа

Равенство (13-7) показывает, что при движении рабочего тела по каналу знаки dw и dp противоположны. Если dp>0, то газ сжимается, и его скорость будет уменьшаться dw 0.
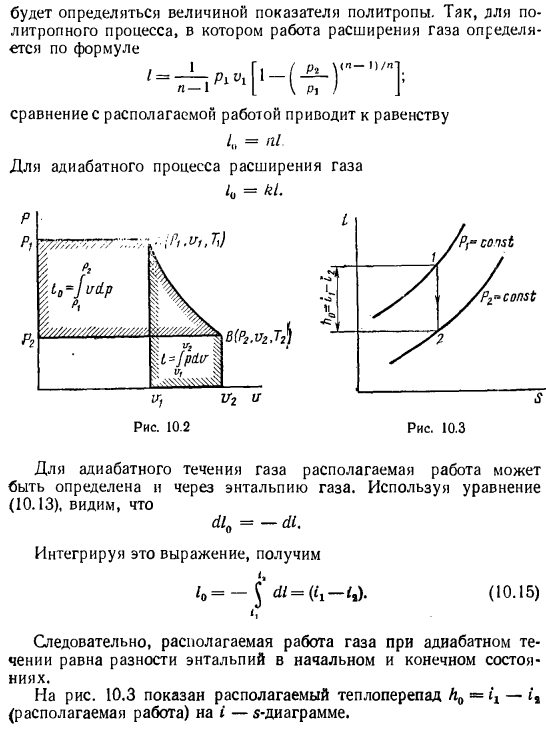
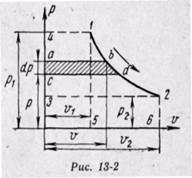
Располагаемую работу при истечении газа можно представить графически на рv-диаграмме. На рис. 13-2 изображен обратимый процесс расширения газа 1-2.
Бесконечно малая располагаемая работа — vdp измеряется элементарной площадкой abdc. Очевидно, вся располагаемая работа в процессе 1-2 будет равна
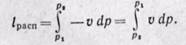
Отсюда приращение кинетической энергии потока газа (располагаемая работа) равно работе внешних сил (p1v1) плюс работа расширения в процессе 1-2 и минус работа (p2v2), затраченная газом на преодоление сопротивления среды, в которую газ вытекает. Она измеряется пл. 1234, ограниченной линией процесса расширения газа, абсциссами крайних точек и осью ординат (р).
Если кривая 1-2 является политропой, то располагаемую работу определяют из уравнения
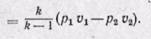
Сравнивая располагаемую работу при
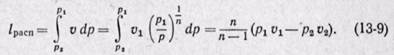
Из уравнения (13-3) следует, что
Располагаемая работа при течении газа может быть получена за счет внешнего тепла и уменьшения энтальпии газа. Это уравнение справедливо как для обратимых, так и для необратимых процессов течения газа с трением.
При адиабатном течении из уравнения (13-5)
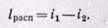
При необратимом истечении газа располагаемая работа при том же перепаде давления будет меньше.
Дата добавления: 2015-04-15 ; просмотров: 1842 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Располагаемая работа газа в потоке
Располагаемая работа газа в потоке
Осборн Рейнольдс впервые показал, что существуют два основных режима движения: ламинарный и турбулентный. Людмила Фирмаль
То есть в обратимом процессе увеличение скорости всегда связано с уменьшением давления, а в обратном случае уменьшение скорости сопровождается увеличением давления. Канал, через который происходит расширение газов, при уменьшении давления (ip 0) и увеличении скорости (wp> 0) называется соплом. Канал, в котором газ сжимается с увеличением давления (dr> 0) и уменьшением скорости (yi> 0), называется диффузионным. Золма. Как видно из уравнения(10.13), необходимым условием для получения доступной работы является перепад давления. Речь идет только о pp. Если во время процесса давление постоянно yp = 0, то доступная работа равна y /₀= 0.
Тот факт, что пограничный слой делит поток на зоны и, таким образом, вносит изменение в режим основного ядра потока, будет подробнее рассматриваться ниже. Людмила Фирмаль
В общем случае одноразовая работа может быть или не быть больше продолжительной работы, но это соотношение равно. Литропический процесс, при котором работа расширения газа определяется уравнением Сравнение с имеющейся работой приводит к равенству FН = Н1. Способ адиабатического расширения газа В случае изолированного потока газа доступная работа может также определяться энтальпией газа. Используя уравнение(10.13)、 ты » = — Си. Если вы интегрируете эту формулу、 1₀= — ^Λ = (1₁-y. (10.15). Таким образом, работа газов, имеющихся в адиабатическом потоке, будет равна разнице между энтальпией начального и конечного состояний.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Располагаемая (полезная) внешняя работа
l 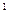





Тепло, участвующее в процессе и идущее на изменение внутренней энергии газа,
q = 



Изобарный процесс
Процесс, протекающий при постоянном давлении ( dp = 0, или p = const ), называют изобарным.
Уравнение процесса
Графическую линию процесса называют изобарой.
Зависимость между параметрами описывается законом Гей-Люссака (объёмы пропорциональны температурам):

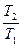
Теплоёмкость процесса – c 
Изменение внутренней энергии одного кг газа определяется по формуле (7.3):






Внешняя работа процесса при v = const определяется из уравнения:
l = 






Располагаемая (полезная) внешняя работа, равная нулю:
l 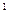

Тепло процесса, равное изменению энтальпии газа:
q = 



Изотермический процесс
Процесс, протекающий при постоянной температуре ( dT = 0, или T = const ), называют изотермическим.
Уравнение процесса
Графическую линию процесса называют изотермой.
Зависимость между параметрами описывается законом Бойля-Мариотта (давления обратно пропорциональны объёмам):


Теплоёмкость процесса c 

Внутренняя энергия и энтальпия газа в процессе не изменяются:


Внешняя работа (расширения или сжатия) процесса определяется из уравнения:
l = 



= 10 









Располагаемая работа, равная работе расширения (сжатия) процесса:
Тепло процесса, равное внешней работе процесса:
Адиабатный процесс
Процесс, протекающий без теплообмена с окружающей средой (dq = 0), называют адиабатным.
где k = 

Графическую линию процесса называют адиабатой.
Зависимости между параметрами в адиабатном процессе:


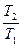




Теплоёмкость процесса, равная 0:
Изменение внутренней энергии одного кг газа определяется по формуле (7.3):






В соответствии с уравнением первого закона термодинамики ( q = 
l = – 











Располагаемая работа в k раз больше работы процесса:
l 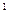
Политропный процесс
Любой процесс идеального газа, в котором теплоёмкость является постоянной величиной, условились называть политропным процессом. Из этого следует, что основные термодинамические процессы (изохорный, изобарный, изотермический и адиабатный), если они протекают при постоянной теплоёмкости, являются частными случаями политропного процесса.
где n = 
любое значение от + 

При известных начальных и конечных параметрах процесса показатель политропы рассчитывается по формуле:
n = 
Графическую линию процесса называют политропой.
Зависимости между параметрами в политропном процессе:


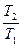




Теплоёмкость политропного процесса может принимать любое значение
от + 

c 


где k = 

Изменение внутренней энергии одного кг газа определяется по формуле (7.3):






Внешняя работа политропного процесса вычисляется по формуле:
l = 


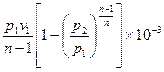
= 
Располагаемая работа в n раз больше работы процесса:
Тепло процесса определяется по формуле:
Изображение процессов в координатах p-v
Равновесные процессы изменения состояния термодинамической системы можно изображать и исследовать графически, используя для этого двухосную систему координат, в которой осью абсцисс является удельный объём v, а осью ординат – давление p. Эта диаграмма получила название pv – диаграмма (рис.7.1).
Следует отметить, что площадь под кривой уравнения процесса на ось v представляет собой работу расширения (сжатия) l, а на ось p – располагаемую работу процесса l 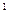






 |
l 




Рис. 7.1. pv – диаграмма.
В координатах pv равновесный изохорный процесс изображается вертикальной прямой линией, изобарный – горизонтальной прямой, изотермический и адиабатный – гиперболическими линиями.



















 |