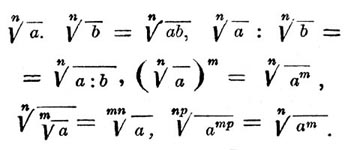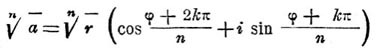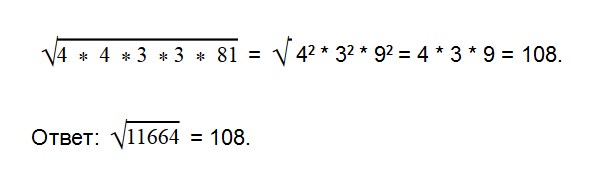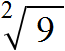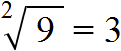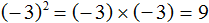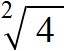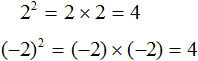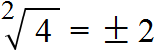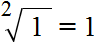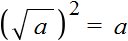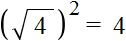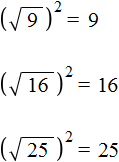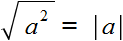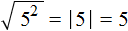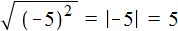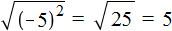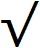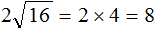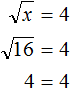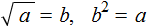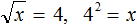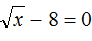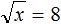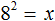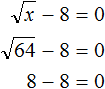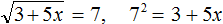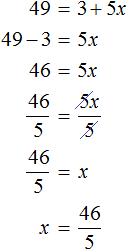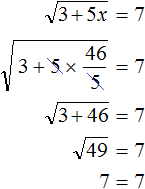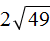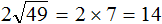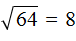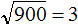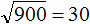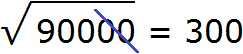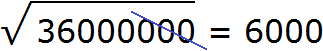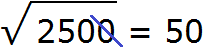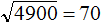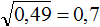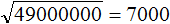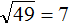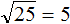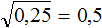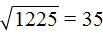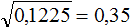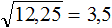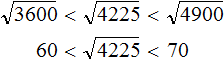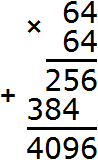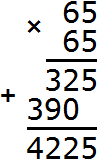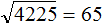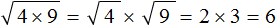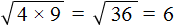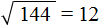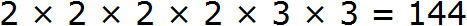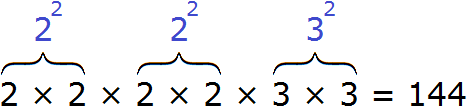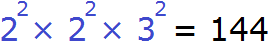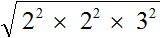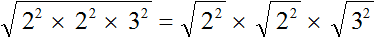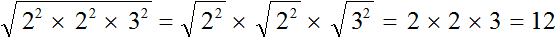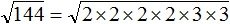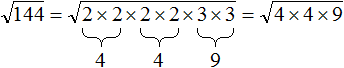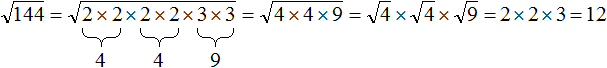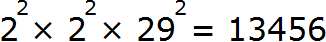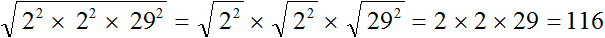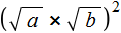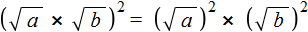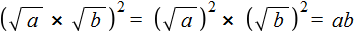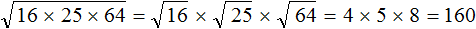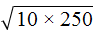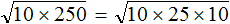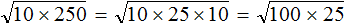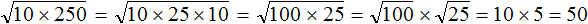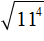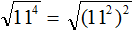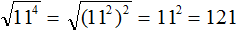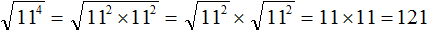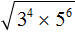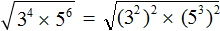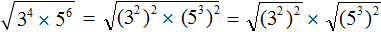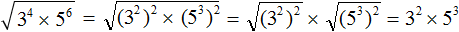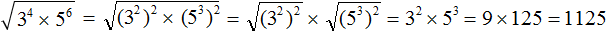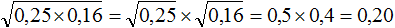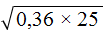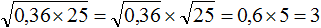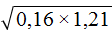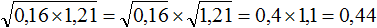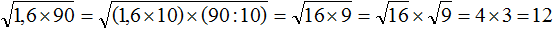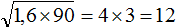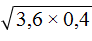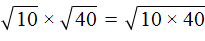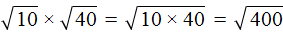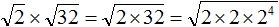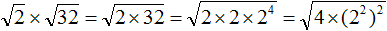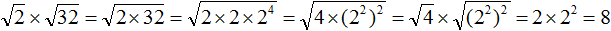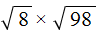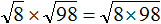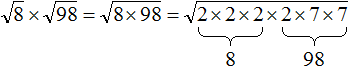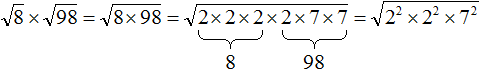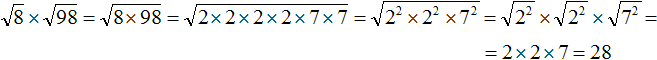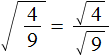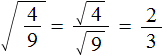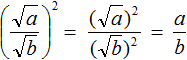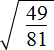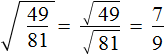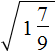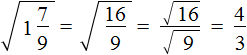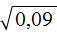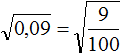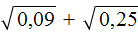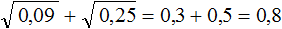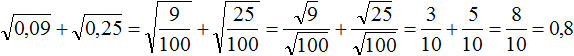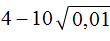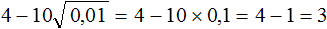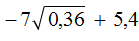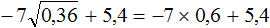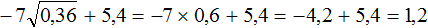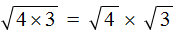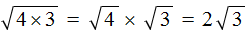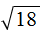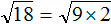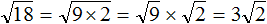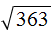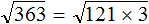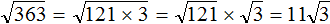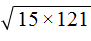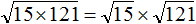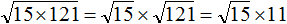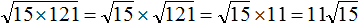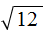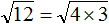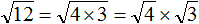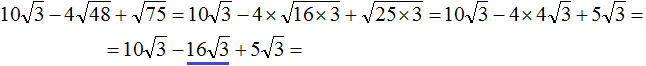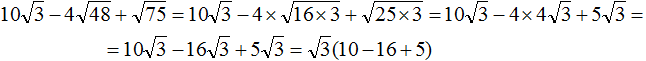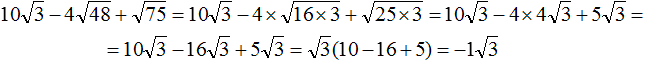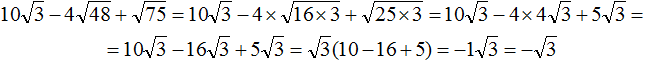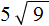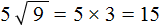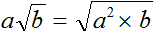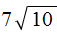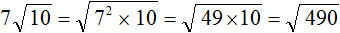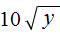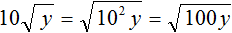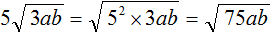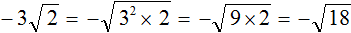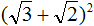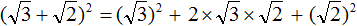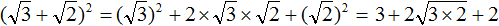Что такое радикалы математика

Радикал в математике

Здесь а называется подкоренным числом, n — показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р. подразумевается число положительное. Алгебраическое выражение, содержащее Р., может подвергаться преобразованиям при помощи формул:

a = r (cos φ + i sin φ), где r > 0.

Для n значений Р. получается выражение

где k = 0, 1, 2. n— 1. В правой части

Полезное

Смотреть что такое «Радикал в математике» в других словарях:

РАДИКАЛ (в математике) — РАДИКАЛ, математический знак (измененное латинское r), которым обозначают действие извлечения корня, а также результат извлечения корня, т. е. число вида … Энциклопедический словарь

Радикал, в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РАДИКАЛ — (лат., radix, radicis корень). 1) Политик, стремящийся к коренным преобразованиям в управлении страны. 2) английские социалисты носят также название радикалов. 3) В органической химии сложные вещества, способные соединяться с другими веществами… … Словарь иностранных слов русского языка

радикал — РАДИКАЛ, а, муж. 1. Сторонник радикализма (в 1 знач.), член радикальной партии. 2. Приверженец крайних, решительных действий, взглядов. | прил. радикалистский, ая, ое. II. РАДИКАЛ, а, муж. 1. В математике: знак, (Ц) обозначающий извлечение корня… … Толковый словарь Ожегова

РАДИКАЛ — (от лат. radicalis коренной) многозначный термин, используемый в разных науках (напр., в химии и математике) и практиках. 1, Сторонник радикальных (крайних, решительных) взглядов и действий, партий, движений. Бескомпромиссный человек. Склонность… … Большая психологическая энциклопедия

Радикал — В Викисловаре есть статья «радикал» Радикал (буквально: «коренной» от лат. radix … Википедия

РАДИКАЛ — Основное значение имеющий отношение к корню. Таким образом: 1. В математике знак (V), выражающий операцию разложения числа, стоящего под ним, на его корни. 2. В социальных/политических терминах описание любой точки зрения или предложения, в… … Толковый словарь по психологии

Центр (в математике) — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Вербицкий, Михаил Сергеевич — В Википедии есть статьи о других людях с такой фамилией, см. Вербицкий. Михаил Вербицкий … Википедия

Абель Нильс Хенрик — (Abel) (1802 1829), норвежский математик. Доказал, что алгебраические уравнения степени выше 4 й в общем случае неразрешимы в радикалах. Изучал интегралы от алгебраических функций (абелевы интегралы). Один из создателей теории эллиптических… … Энциклопедический словарь

Источник

Радикал, в математике

Полезное

Смотреть что такое «Радикал, в математике» в других словарях:

РАДИКАЛ (в математике) — РАДИКАЛ, математический знак (измененное латинское r), которым обозначают действие извлечения корня, а также результат извлечения корня, т. е. число вида … Энциклопедический словарь

Радикал в математике — Один из корней двучленного уравнения xn = а называется радикалом и обозначается Здесь а называется подкоренным числом, n показателем корня. Р. называется иногда корнем. В начальной алгебре подкоренное число предполагается положительным и под Р.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

РАДИКАЛ — (лат., radix, radicis корень). 1) Политик, стремящийся к коренным преобразованиям в управлении страны. 2) английские социалисты носят также название радикалов. 3) В органической химии сложные вещества, способные соединяться с другими веществами… … Словарь иностранных слов русского языка

радикал — РАДИКАЛ, а, муж. 1. Сторонник радикализма (в 1 знач.), член радикальной партии. 2. Приверженец крайних, решительных действий, взглядов. | прил. радикалистский, ая, ое. II. РАДИКАЛ, а, муж. 1. В математике: знак, (Ц) обозначающий извлечение корня… … Толковый словарь Ожегова

РАДИКАЛ — (от лат. radicalis коренной) многозначный термин, используемый в разных науках (напр., в химии и математике) и практиках. 1, Сторонник радикальных (крайних, решительных) взглядов и действий, партий, движений. Бескомпромиссный человек. Склонность… … Большая психологическая энциклопедия

Радикал — В Викисловаре есть статья «радикал» Радикал (буквально: «коренной» от лат. radix … Википедия

РАДИКАЛ — Основное значение имеющий отношение к корню. Таким образом: 1. В математике знак (V), выражающий операцию разложения числа, стоящего под ним, на его корни. 2. В социальных/политических терминах описание любой точки зрения или предложения, в… … Толковый словарь по психологии

Центр (в математике) — Для общего описания теории групп см. Группа (математика) и Теория групп. Курсив обозначает ссылку на этот словарь. # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У … Википедия

Вербицкий, Михаил Сергеевич — В Википедии есть статьи о других людях с такой фамилией, см. Вербицкий. Михаил Вербицкий … Википедия

Абель Нильс Хенрик — (Abel) (1802 1829), норвежский математик. Доказал, что алгебраические уравнения степени выше 4 й в общем случае неразрешимы в радикалах. Изучал интегралы от алгебраических функций (абелевы интегралы). Один из создателей теории эллиптических… … Энциклопедический словарь

Источник

Что такое квадратный корень

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

Это два нетождественных друг другу выражения.

Из выражения x 2 = 16 следует, что:

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Извлечение корней

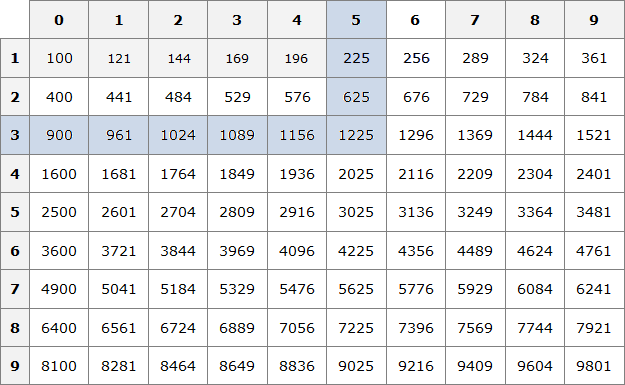
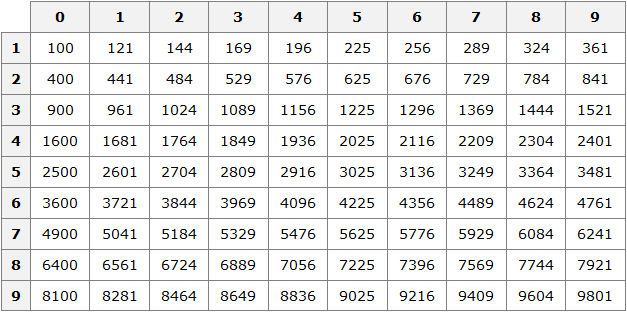
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

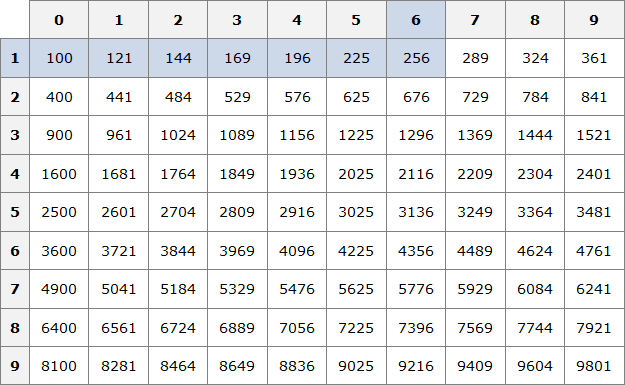
Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Ищем в таблице число 7396.

Ищем в таблице число 9025.

Ищем в таблице число 1600.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

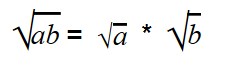Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

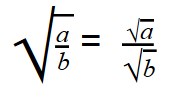Примеры:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

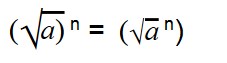Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Извлечь корень из большого числа можно разными способами — вот один из них.

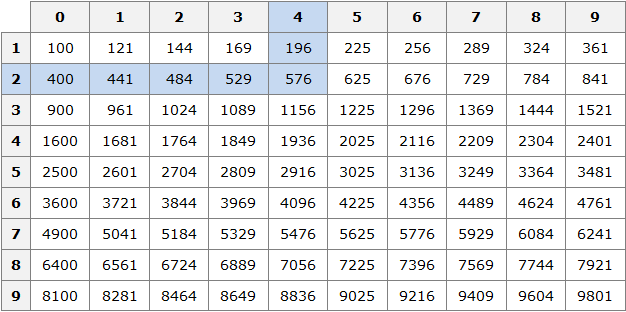
Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10

Источник

Квадратный корень

Основные сведения

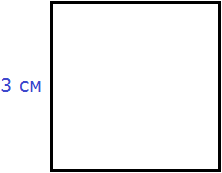
Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.

Найдём площадь квадрата, длина стороны которого 3 см

S = 3 2 = 9 см 2

Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.

Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.

Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.

Введём для работы с корнями новые обозначения.

Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)

Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)

Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:

Значит квадрат площадью 9 см 2 имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.

Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9

Получается, что выражение 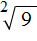имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.

Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.

Например, извлечём квадратный корень из числа 4

Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4

Поэтому ответ к выражению вида 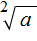записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.

Запишем ответ к выражению 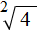с плюсом и минусом:

Определения

Дадим определение квадратному корню.

Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16

Корень 4 можно обозначить через радикал 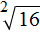так, что .

Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16

Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.

В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.

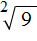
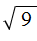
Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи можно использовать запись. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.

Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:

Это по причине того, что единица во второй степени равна единице:

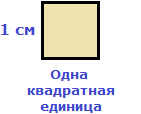
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:

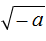
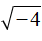
Выражение вида смысла не имеет. Например, не имеет смысла выражение , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.

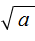
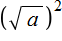
Если выражение вида возвести во вторую степень, то есть если записать , то это выражение будет равно подкореннóму выражению a

Например, выражение 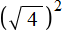равно 4

Это потому что выражение 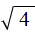равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.

Корень из квадрата числá равен модулю этого числá:

Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5

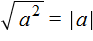
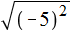
Действительно, если не пользуясь правилом , вычислять выражение обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5

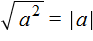
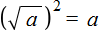
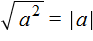
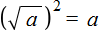
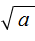
Не следует путать правило с правилом . Правило верно при любом a, тогда как правило верно в том случае, если выражение имеет смысл.

В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:

Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.

Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.

Примеры извлечения квадратных корней

Рассмотрим несколько простых примеров на извлечение квадратных корней.

Пример 1. Извлечь квадратный корень √36

Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 6 2 = 36

Пример 2. Извлечь квадратный корень √49

Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 7 2 = 49

В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:

Пример 3. Извлечь квадратный корень √100

Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.

Пример 3. Извлечь квадратный корень √256

Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.

Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.

Пример 4. Найти значение выражения 2√16

Пример 7. Решить уравнение

В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.

Значение переменной x равно 16, поскольку 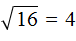. Значит корень уравнения равен 16.

Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом .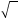

Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.

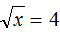
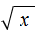
Применим равенство b 2 = a к нашему примеру . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем , а именно переменная x

Пример 8. Решить уравнение

Перенесем −8 в правую часть, изменив знак:

Возведем правую часть во вторую степень и приравняем её к переменной x

Пример 9. Решить уравнение

Воспользуемся определением квадратного корня:

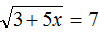
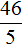
Корень уравнения равен . Выполним проверку, подставив его в исходное уравнение:

Пример 10. Найти значение выражения

В этом выражении число 2 умножается на квадратный корень из числа 49.

Сначала нужно извлечь квадратный корень и перемножить его с числом 2

Приближённое значение квадратного корня

Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.

А извлечь квадратный корень 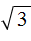нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.

Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.

Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.

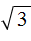
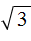
Найдём значение корня приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня будет представлять собой десятичную дробь, у которой после запятой одна цифра.

Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:

Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2

А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:

Точные значения корней √1 и √4 известны. Это числа 1 и 2

Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.

Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1

Проверим тогда дробь 1,8

Проверим тогда дробь 1,7

В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.

Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8

Проверим дробь 1,74

Проверим тогда дробь 1,73

Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:

√3 = 1,732 (вычислено с точностью до тысячных)

√3 = 1,7320 (вычислено с точностью до десятитысячных)

√3 = 1,73205 (вычислено с точностью до ста тысячных).

Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:

Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.

В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.

Приближенное значение квадратного корня с недостатком или избытком

Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.

Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:

Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.

Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2

Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:

Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.

Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:

Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1

Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1

Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01

Границы, в пределах которых располагаются корни

Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].

Пример 2. Извлечь квадратный корень из числа 49

Пример 2. Извлечь квадратный корень из числа 1

Пример 3. Извлечь квадратный корень из числа 100

Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:

1 2 = 1
2 2 = 4
3 2 = 9
4 2 = 16
5 2 = 25
6 2 = 36
7 2 = 49
8 2 = 64
9 2 = 81
10 2 = 100

И обратно, следует знать значения квадратных корней этих квадратов:

Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.

А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:

Тогда можно сделать следующий вывод:

Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.

Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3

Пример 2. Извлечём квадратный корень из числа 90000

Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:

Пример 3. Извлечем квадратный корень из числа 36000000

Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:

Пример 4. Извлечем квадратный корень из числа 2500

Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:

Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.

Например, 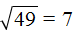. Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:

И наоборот, если в равенстве 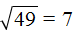уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:

Пример 2. Увеличим в равенстве 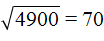подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз

Пример 3. Уменьшим в равенстве 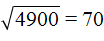подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз

Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:

Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве 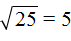подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:

В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.

Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, .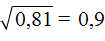

Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.

Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].

В этом случае применяется таблица квадратов:

Видим, что это число 24. Значит .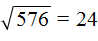

Извлечем квадратный корень из числа 432 с точностью до десятых.

В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.

Проверим, например, число 20,8. Для этого возведём его в квадрат:

Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.

Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:

Корень 64 не годится. Проверим корень 65

Получается 4225. Значит 65 является корнем числа 4225

Тождественные преобразования с квадратными корнями

Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.

Квадратный корень из произведения

Квадратный корень из произведения это выражение вида 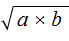, где a и b некоторые числа.

Например, выражение 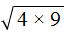является квадратным корнем из произведения чисел 4 и 9.

Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.

Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12

Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.

Итак, разлóжим число 144 на простые множители:

Получили следующее разложение:

В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.

В результате будем иметь следующее разложение:

Теперь можно извлекáть квадратный корень из разложения числа 144

Применим правило извлечения квадратного корня из произведения:

Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.

Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.

затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:

Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:

С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.

Итак, разложим число 13456 на простые множители:

Теперь будем извлекать квадратный корень из разложения числа 13456

Докажем равенство 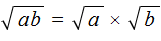. Для этого воспользуемся определением квадратного корня.

Итак, выпишем правую часть равенства 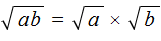и возведём ее во вторую степень:

Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:

Значит равенство 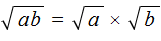справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.

Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:

, при a ≥ 0 и b ≥ 0, c ≥ 0.

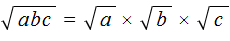
Пример 1. Найти значение квадратного корня

Запишем корень 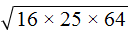в виде произведения корней, извлечём их, затем найдём значение полученного произведения:

Пример 2. Найти значение квадратного корня

Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100

Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:

Пример 3. Найти значение квадратного корня

Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:

Далее возводим число 11 во вторую степень и получаем окончательный ответ:

Пример 4. Найти значение квадратного корня

Далее используем правило извлечения квадратного кóрня из произведения:

Далее используем правило извлечения квадратного кóрня из квадрата числа:

Вычислим произведение получившихся степеней и полýчим окончательный ответ:

Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения

Запишем корень 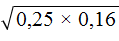в виде произведения корней, извлечём их, затем найдём значение полученного произведения:

Пример 6. Найти значение квадратного корня

Пример 7. Найти значение квадратного корня

Например, произведение 8 × 4 равно 32

Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.

Например, извлечём квадратный корень из произведения 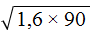. Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.

Запишем полное решение данного примера:

Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:

Пример 9. Найти значение квадратного корня

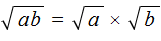
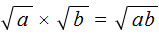
Если в равенстве поменять местами левую и правую часть, то полýчим равенство . Это преобразовáние позволяет упрощáть вычисление некоторых корней.

Например, узнáем чему равно значение выражения .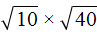

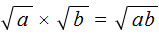
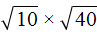
Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом , то есть заменим выражение из двух корней на выражение с одним корнем, под которым будет произведение из чисел 10 и 40

Теперь найдём значение произведения, находящегося под корнем:

А квадратный корень из числа 400 извлекается. Он равен 20

Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.

Например, найдём значение выражения .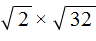

Воспользуемся правилом

Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 2 4 предстáвим в виде степени с показателем 2

Теперь воспóльзуемся правилом 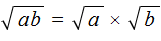и вычислим окончательный ответ:

Пример 12. Найти значение выражения

Воспользуемся правилом

Теперь воспользуемся правилом 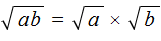и вычислим окончательный ответ:

Квадратный корень из дроби

Вычислим квадратные корни в числителе и знаменателе:

Докáжем, что равенство является верным.

Возведём правую часть во вторую степень. Если в результате полýчим дробь 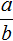, то это будет означать, что равенство верно:

Пример 1. Извлечь квадратный корень

Воспользуемся правилом извлечения квадратного корня из дроби:

Пример 2. Извлечь квадратный корень

Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:

Пример 3. Извлечь квадратный корень

Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:

Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:

Пример 4. Найти значение выражения

Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:

Также можно воспользоваться правилом извлечения квадратного корня из дроби:

В данном примере первый способ оказался проще и удобнее.

Пример 5. Найти значение выражения

Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4

Пример 6. Найти значение выражения

Сначала найдём значение квадратного корня 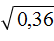. Он равен 0,6 поскольку 0,6 2 = 0,36

Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:

Вынесение множителя из-под знака корня

В некоторых задачах может быть полезным вынесение множителя из-под знака корня.

Рассмотрим квадратный корень из произведения . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения: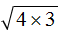

В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение 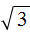оставим без изменений:

Это и есть вынесение множителя из-под знака корня.

На практике подкореннóе выражение чаще всего требуется разложить на множители.

Пример 2. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:

Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:

Пример 3. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:

Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:

Пример 4. Вынести множитель из-под знака корня в выражении

Воспользуемся правилом извлечения квадратного корня из произведения:

Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:

Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √ 15 и 11 местами:

Пример 5. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 4 и 3

Воспользуемся правилом извлечения квадратного корня из произведения:

Извлечём корень из числа 4, а выражение √3 остáвим без изменений:

Пример 6. Упростить выражение

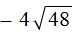
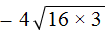
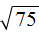
Предстáвим второе слагаемое в виде . А третье слагаемое предстáвим в виде

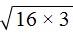
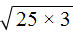
Теперь в выражениях и вынесем множитель из-под знака корня:

Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:

Вычислим содержимое скобок, полýчим −1

Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3

Внесение множителя под знак корня

Рассмотрим следующее выражение:

В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.

Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.

Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15

Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.

Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:

Итак, если данó выражение 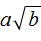, и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:

Пример 1. Внести множитель под знак корня в выражении

Возведём число 7 во вторую степень и внесём его под знак корня:

Пример 2. Внести множитель под знак корня в выражении

Возведём число 10 во вторую степень и внесем его под знак корня:

Пример 3. Внести множитель под знак корня в выражении

Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида 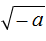не имеет смысла.

Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.

Пример 4. Внести множитель по знак корня в выражении

В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:

Пример 5. Выполнить возведéние в степень в следующем выражении:

Воспользуемся формулой квадрата суммы двух выражений:

Теперь необходимо упростить получившееся выражение.

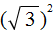
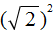
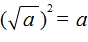
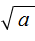
Для выражений и применим правило . Ранее мы говорили, что если выражение вида возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.

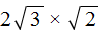
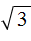
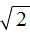
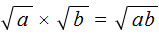
А в выражении для множителей и применим правило . То есть заменим произведение корней на один общий корень:

Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом вычислить произведение, которое под кóрнем:

Источник