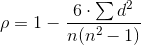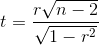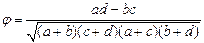Что такое ранговая корреляция
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
КРИТЕРИЙ СПИРМЕНА
– это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

1. История разработки коэффициента ранговой корреляции
Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.
2. Для чего используется коэффициент Спирмена?
3. В каких случаях можно использовать коэффициент Спирмена?
В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.
Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).
Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.
4. Как рассчитать коэффициент Спирмена?
Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
5. Как интерпретировать значение коэффициента Спирмена?
Также для оценки тесноты связи может использоваться шкала Чеддока:
| Абсолютное значение rxy | Теснота (сила) корреляционной связи |
| менее 0.3 | слабая |
| от 0.3 до 0.5 | умеренная |
| от 0.5 до 0.7 | заметная |
| от 0.7 до 0.9 | высокая |
| более 0.9 | весьма высокая |
Ранговая корреляция



В отличие от этого метода, метод ранговой корреляции (корреляция Спирмена) применим к любым количественно измеренным или ранжированным данным. Этот метод способен, в отличие от других, измерять согласованность изменения разных признаков у одного испытуемого или выявлять совпадения индивидуальных ранговых показателей у двух испытуемых; или у испытуемого и усредненный показатель некой группы; или какие-либо показатели в сравнении двух групп.
Метод ранговой корреляции Спирмена позволяет определить силу и направление корреляционной связи между двумя признаками (или двумя иерархиями признаков).
Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы.
Такими рядами могут быть:
а) Два признака, измеренные в одной и той же группе переменных (наиболее часто в этом качестве выступает группа людей, которых принято тогда именовать испытуемыми или респондентами. Естественно, под переменными подразумеваются не сами люди, а данные ими ответы на те или иные вопросы.)
б) две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (скажем, по ответам на пункты анкеты или теста).
в) Две групповые иерархии признаков (например, соответствие каких-либо выборов, сделанных одной группой людей выборам другой группы).
г) Индивидуальная и групповая иерархии признаков (например, сопоставление индивидуальной иерархии жизненных ценностей сотрудника усредненному мнению группы на этот же счет; сопоставление последовательности товаров, которые приобрели бы (в среднем) жители города А и города Б при условии получения премии, на которую заранее не рассчитывали.)
Ограничения метода ранговой корреляции
По каждой переменной должно быть представлено не менее 5 наблюдений. Верхняя граница выборки – меньше или равна 40. Коэффициент ранговой корреляции Спирмена rs при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения. В идеале оба коррелируемых ряда должны представлять собой две последовательности несовпадающих значений. В случае несоблюдения такого условия вносится поправка на одинаковые ранги (будет дано ниже). Помимо этих ограничений, следует так же помнить об ограничениях корреляционного метода вообще – невозможность обнаружения причинной связи между явлениями.
Алгоритм расчета ранговой корреляции:
1) Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные А и В.
2) Проранжировать значения переменной А, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. Занести ранги во 2-й столбец таблицы по порядку номеров признаков. (В 1-м к тому моменту уже находятся номера или имена исследуемых признаков.)
3) Проранжировать значения переменной В и занести в 3-й столбец таблицы по порядку номеров.
4) Подсчитать разности d между рангами А и В по каждой строке и результаты занести в 4-й столбец таблицы.
5) Возвести каждую разность из столбца 4 в квадрат, и результаты занести в столбец №5.
6) Подсчитать сумму квадратов из столбца №5.
7) При наличии одинаковых рангов, рассчитать поправки: Тa =S(a 3 – a)/12 и Тb =S(b 3 – b)/12
8) Рассчитать коэффициент ранговой корреляции rs при отсутствии одинаковых рангов – по формуле а; при наличии – по формуле б:
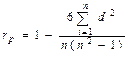
Где: Sd 2 – квадратов разностей между рангами; Тa и Тb – поправки на одинаковые ранги;
N – количество признаков, участвовавших в ранжировании.
При 0,05% уровне значимости:
| N (df=N-2) | Уровень значимости |
| 0,05 (95%) | 0,01 (99%) |
| 0,63 | 0,77 |
| 0,44 | 0,56 |
Образец таблицы для внесения данных:
| Наименование признака | Ранги переменной А (по порядку) | Ранги переменной В (по порядку) | Разница между значениями двух предыдущих столбцов №2 и №3 | Квадрат значений предыдущего столбца №4 |
Преимущество r-Спирмена по сравнению с r-Пирсона — в большей чувствительности к связи в случае:
· существенного отклонения распределения хотя бы одной переменной от нормального вида (асимметрия, выбросы);
· криволинейной (монотонной) связи
Недостаток r-Спирмена по сравнению с r-Пирсона — в меньшей чувствительности к связи в случае несущественного отклонения распределения обеих переменных от нормального вида.
Корреляция бинарных данных
Если обе переменные представлены в бинарной шкале (0,1), для изучения связи между ними можно применять φ-коэффициент сопряженности ( если для каждой переменной количество 0 и 1 приблизительно одинаковое).
Рассмотрим случай изучения связи двух бинарных переменных. Примеры таких переменных: пол (мужской, женский), образование (среднее, высшее), тревожность (низкая, высокая), успешность (низкая, высокая) и т. д. При изучении связей между бинарными переменными обычно строят четырехклеточные таблицы сопряженности:
| Признак X | Итог | ||
| Признак Y | а | b | a + b |
| с | d | с + d | |
| Итог | а + с | b + d | N |
В этом случае допустимо применение r-Пирсона непосредственно к исходным данным — двум бинарным переменным, принимающим значение 0 или 1, измеренным для каждого члена выборки численностью N. Результат применения r-Пирсона к двум бинарным переменным называется «фи-коэффициентом сопряженности» (Phi). Если данные представлены в четырехклеточной таблице сопряженности, то применяется формула, существенно упрощающая расчеты, но дающая аналогичный результат:
Пример. Исследовалась связь семейного положения студенток (X: 0 — холостая, 1 — замужем) и их академической успеваемости (Y: 0 — закончила вуз, 1 — отчислена).
Таблица сопряженности для этих данных:
Вычислим ср-коэффициент сопряженности:
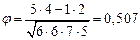
Получена умеренная положительная взаимосвязь: холостые студентки чаще заканчивают вуз, а замужние — чаше отчисляются. Отметим, что тот же самый результат был бы получен при применении формулы r-Пирсона непосредственно к исходным данным.
Ранговая корреляция
Ранговая корреляция [rank correlation] — мера зависимости между случайными величинами (наблюдаемыми признаками, переменными), когда эту зависимость невозможно определить количественно с помощью обычного коэффициента корреляции (см. Корреляция). Процедура установления Р.к. заключается в упорядочении изучаемых объектов в отношении некоторого признака, т.е. им приписываются порядковые номера — ранги (по два номера в соответствии с двумя наблюдаемыми признаками, между которыми исследуется корреляция). Например, наибольшее значение для переменной обозначается номером 1, второе по величине — номером 2 и т.д. Наиболее распространен коэффициент Р.к. (коэффициент Спирмена):
где Di — разница между рангами, присвоенными каждой из переменных i (i = 1, …, n), N — размер выборки. Этот коэффициент принимает значения между +1 и –1, показывая тесноту и направление связи между исследуемыми величинами. Метод Р.к. — один из т.н. непараметрических методов математической статистики.
Смотреть что такое «Ранговая корреляция» в других словарях:
РАНГОВАЯ КОРРЕЛЯЦИЯ — (rank correlation) Метод проверки зависимости между двумя переменными с помощью определения корреляции их ранговых порядков. Этот метод может быть использован, если предполагается, что зависимость монотонно возрастает или снижается, но форма ее… … Экономический словарь
ранговая корреляция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] ранговая корреляция Мера зависимости между случайными величинами (наблюдаемыми признаками, переменными), когда эту зависимость невозможно определить… … Справочник технического переводчика
СПИРМЕНА, РАНГОВАЯ КОРРЕЛЯЦИЯ — См. корреляция, ранговых порядков … Толковый словарь по психологии
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
КОРРЕЛЯЦИЯ РАНГОВАЯ — англ. correlation, rank; нем. Rangkorrelation. Корреляция, измеряющая степень соответствия упорядочения совокупности объектов по двум переменным. см. КОРРЕЛЯЦИЯ ЛИНЕЙНАЯ. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
КОРРЕЛЯЦИЯ РАНГОВАЯ — корреляция двух ранговых переменных ( также Шкала измерительная). С поправкой на связные ранги может применяться к любым порядковым переменным. К.Р. называется прямой или положительной, если с повышением ранга объекта по одной переменной… … Социология: Энциклопедия
КОРРЕЛЯЦИЯ РАНГОВАЯ — англ. correlation, rank; нем. Rangkorrelation. Корреляция, измеряющая степень соответствия упорядочения совокупности объектов по двум переменным. См. КОРРЕЛЯЦИЯ ЛИНЕЙНАЯ … Толковый словарь по социологии
КОРРЕЛЯЦИЯ, КЕНДАЛЛА РАНГОВАЯ (и КЕНДАЛЛА, ЧАСТИЧНАЯ РАНГОВАЯ) — См. Кендалла тесты … Толковый словарь по психологии
Что такое ранговая корреляция
Пример 176. Получить выборочный коэффициент ранговой корреляции Спирмена
(использовали формулы конечных сумм из [15. С. 72-74]).
Покажем эффективность использования полученного коэффициента ранговой корреляции Спирмена на следующем примере.
Пример 177. Знания 10 студентов проверены по двум тестам, А и В. Оценки по стобалльной системе оказались следующими:
| Тест А | 95 90 87 84 75 70 61 60 58 55 |
| Тест В | 92 94 83 79 58 61 47 72 62 68 |
Найдите выборочный коэффициент ранговой корреляции Спирмена между оценками по двум тестам.
Решение. Запишем ранги студентов по тестам и квадраты их разностей:
| ранг по тесту А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ранг по тесту В | 2 | 1 | 3 | 4 | 9 | 8 | 10 | 5 | 7 | 6 |
| 1 | 1 | 0 | 0 | 16 | 4 | 9 | 9 | 4 | 16 |
В психолого-педагогических исследованиях достаточно часто используется ранговая корреляция Спирмена, поэтому приведем здесь алгоритм ее применения и пример из диссертационного исследования по психологии.
Проранжировать значения второй переменной по тем же правилам и занести соответствующие ранги во второй столбец.
Подсчитать разности между рангами и по каждой строке и занести их в третий столбец.
При наличии одинаковых рангов рассчитать поправки:
Рассчитать коэффициент ранговой корреляции Спирмена по формуле:
б) при наличии одинаковых рангов
Пример 178. Найти коэффициент ранговой корреляции Спирмена по связи эмоционального состояния и зрительной памяти после иппотерапии по результатам исследования.
| Количество выборов, соответствующее положительному эмоциональному состоянию | Зрительная память | ||||
| баллы | ранг | баллы | ранг | ||
| 3 | 19.5 | 6 | 22 | -2,5 | 6,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 1 | 3,5 | 4 | 7 | -3,5 | 12,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 3 | 19,5 | 6 | 22 | -2,5 | 6,25 |
| 2 | 10,5 | 3 | 3 | 7,5 | 56,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 3 | 19,5 | 6 | 22 | -2,5 | 6,25 |
| 2 | 10,5 | 6 | 22 | 11,5 | 132,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 3 | 19,5 | 6 | 22 | -2,5 | 6,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 3 | 19,5 | 4 | 7 | 12,5 | 156,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 1 | 3,5 | 4 | 7 | -3,5 | 12,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 1 | 3,5 | 3 | 3 | 0,5 | 0,25 |
| 2 | 10,5 | 5 | 14 | -3,5 | 12,25 |
| 3 | 19,5 | 5 | 14 | 5,5 | 30,25 |
| 620 | |||||
| r = | 0,611 | ||||
Связь между двумя качественными признаками можно оценить, используя выборочный коэффициент ранговой корреляции Кендалла :
Пример 179. Определите степень связи итогов чемпионата России по футболу в премьер-лиге и результаты первого круга 2002 года.
| Команда | Локо | ЦСКА | Спартак | Торпедо | Кр. Сов. | Сатурн | Шинник | Динамо | Ротор | Зенит |
| Итог 2002 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| круг | 1 | 2 | 3 | 10 | 6 | 4 | 8 | 7 | 5 | 9 |
Решение. Определим степень связи по выборочному коэффициенту ранговой корреляции Кендалла.
и между итогом чемпионата и результатом первого круга существует прямая средней тесноты связь.
Если статистическая информация о многомерном признаке представлена в порядковой шкале, то измерение парных связей осуществляется через коэффициенты ранговой корреляции Кендалла или Спирмена.
Пример 180. Три арбитра оценили мастерство 10 фигуристов, в итоге были получены три последовательности рангов:
| Ранг арбитра А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранг арбитра В | 3 | 10 | 6 | 2 | 8 | 5 | 7 | 9 | 1 | 4 |
| Ранг арбитра С | 6 | 3 | 1 | 2 | 9 | 4 | 5 | 7 | 10 | 8 |
Найдите матрицу ранговой корреляции Спирмена и пару арбитров, оценки которых наиболее согласуются.
Поскольку коэффициент является максимальным, то оценки арбитров А и С наиболее согласуются.
I. 351. Специалисты двух заводов проранжировали 8 факторов, влияющих на ход технологического процесса. В итоге были получены две последовательности рангов:
Определите, согласуются ли мнения специалистов различных заводов, используя коэффициент ранговой корреляции Спирмена.
352. Получены рейтинги строительства жилья в регионах Центрального федерального округа в 2001 и 2002 годах:
Найдите коэффициент ранговой корреляции Спирмена для строительства жилья в 2001 и 2002 годах по 10 регионам РФ.
353. Установить, как коррелируют результаты чемпионата России по хоккею в суперлиге по итогам двух кругов чемпионата 2001 и 2002 годов:
| Команда | Ак Барс | Авангард | Мет. М. | Лада | Сев. Ч. | Неф. | Локо. | Мечел | Амур | Мет. Нк. | ЦСКА | Динамо |
| Место 2001 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Место 2002 | 4 | 3 | 7 | 5 | 2 | 11 | 1 | 12 | 9 | 8 | 10 | 6 |
354. По данным статистического сборника «Социальная сфера регионов Центральной России», денежные доходы и потребительские расходы в расчете на душу населения в ноябре 2002 года составили:
| Области | Брянская | Владимирская | Ивановская | Калужская | Костромская | Московская | Орловская | Рязанская | Тверская | Ярославская |
| Доходы (руб.) | 2542 | 2256 | 1793 | 2633 | 2440 | 3631 | 2614 | 2726 | 2416 | 3630 |
| Расходы (руб.) | 1666 | 1259 | 1241 | 1693 | 1459 | 2788 | 1868 | 1673 | 1620 | 1902 |
Проранжируйте полученные данные и найдите коэффициент ранговой корреляции Кенделла для доходов и расходов на душу населения в областях Центрального федерального округа.
355. За пять лет ввод общей площади (в тыс. кв. м) жилых домов в области и в городе Ярославле характеризуются следующими данными:
| Год | 1997 | 1998 | 1999 | 2000 | 2001 |
| Яр. область | 222,6 | 231,7 | 221 | 130,6 | 162,3 |
| г. Ярославль | 118,6 | 119,7 | 113,3 | 66,5 | 89 |
Что можно сказать о степени зависимости ввода жилья в Ярославской области и в городе Ярославле?
: 6, 3, 4, 2, 1, 10, 7, 8, 9, 5, 11, 12.
II. 357. Четыре преподавателя расположили 10 студентов по результатам текущей успеваемости по алгебре, аналитической геометрии, общей физике и истории отечества:
Найдите матрицу ранговой корреляции Кенделла и два предмета, оценки по которым наиболее согласуются.
358. Докажите, что если между качественными признаками А и В имеется «полная прямая зависимость» («противоположная зависимость»), то выборочные коэффициенты ранговой корреляции Спирмена и Кендалла равны единице (минус единице).
III. 359. Найдите корреляционную матрицу для характеристики директорского и учительского корпуса Ярославской области по стажу педагогической работы.
| всего | До 2 лет | 2-5 лет | 5-10 лет | 10-20 лет | свыше 20 лет | пенсионеры | |||||||
| Кол-во | % | Кол-во | % | Кол-во | % | Кол-во | % | Кол-во | % | Кол-во | % | ||
| Дир. СШ | 289 | 6 | 2,1 | 7 | 2,4 | 21 | 7,3 | 59 | 20,4 | 198 | 67,8 | 63 | 21,8 |
| Зам. дир. СШ | 687 | 28 | 4,1 | 28 | 4,0 | 67 | 9,8 | 241 | 35,1 | 323 | 47,0 | 63 | 9,2 |
| Учит. гуманит. и ест.-мат циклов | 6343 | 462 | 7,3 | 411 | 6,5 | 843 | 13,3 | 2039 | 32,1 | 2588 | 40,8 | 766 | 12.1 |
| Учит.др. спец. | 1984 | 135 | 6,8 | 119 | 6,0 | 299 | 15,0 | 684 | 34,5 | 747 | 37,7 | 141 | 7,1 |
360. Найдите корреляционные матрицы по производству продуктов животноводства (в тыс. тонн и в % к 2001 году) в хозяйствах 10 регионов РФ в 2002 году.
| Области | Скот и птица | Молоко | Яйца | ||||||
| Тыс. тонн | В % к 2001 г. | рост | Тыс. тонн | В % к 2001 г. | рост | Тыс. тонн | В % к 2001 г. | рост | |
| Орловская | 56,7 | 108,6 | 279,6 | 98,9 | 202 | 92 | |||
| Московская | 103,4 | 106,4 | 778,5 | 97,8 | 1238 | 88 | |||
| Ярославская | 32,5 | 105,5 | 291 | 99,6 | 384 | 105,8 | |||
| Владимирская | 42,7 | 105,3 | 283 | 100,3 | 333 | 107,3 | |||
| Калужская | 40,5 | 103,3 | 238 | 93,8 | 171 | 124 | |||
| Тульская | 51,0 | 102,8 | 282 | 99,8 | 401 | 100,6 | |||
| Рязанская | 41,7 | 100,3 | 380 | 102,5 | 332 | 98,3 | |||
| Тверская | 45,9 | 99,7 | 373 | 99,4 | 385 | 102 | |||
| Ивановская | 27,6 | 99,6 | 194 | 97,7 | 204 | 103,7 | |||
| Костромская | 30,4 | 97,5 | 195 | 101 | 365 | 112,1 | |||
Какая из полученных корреляционных матриц лучше отражает связь при производстве продуктов животноводства в регионах РФ?