Что такое расходящиеся ряды
РАСХОДЯЩИЙСЯ РЯД
— ряд, у к-рого последовательность частичных сумм не имеет конечного предела. Напр., ряды
Р. р. стали появляться в работах математиков 17-18 вв. Л. Эйлер (L. Euler) первым пришел к выводу, что нужно ставить вопрос, не чему равна сумма, а как определить сумму Р. р., и нашел подход к решению этого вопроса, близкий к современному. Р. р. до кон. 19 в. не находили применения и были почти забыты. Накопление к кон. 19 в. различных фактов математич. анализа вновь пробудило интерес к Р. р. Стал выдвигаться вопрос о возможности суммирования рядов в нек-ром смысле, отличном от обычного.
П р и м е р ы. 1) Если перемножить два ряда
сходящихся соответственно к А и В, то полученный в результате перемножения ряд
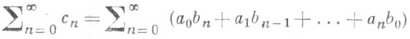
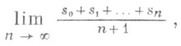
то в этом смысле ряд (1) всегда будет сходиться (т. е. предел в (2) будет существовать) и его сумма в этом смысле равна С=АВ.
2) Ряд Фурье функции f(х), непрерывной в точке х 0 (или имеющей разрыв 1-го рода), может расходиться в этой точке. Если же сумму ряда определить по формуле (2), то в этом смысле ряд Фурье такой функции всегда будет сходиться и его сумма в этом смысле равна f(x 0 ) (или соответственно 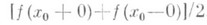

сходится для 



Полезное
Смотреть что такое «РАСХОДЯЩИЙСЯ РЯД» в других словарях:
расходящийся ряд — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN divergent series … Справочник технического переводчика
расходящийся ряд — diverguojančioji eilutė statusas T sritis fizika atitikmenys: angl. divergent series vok. divergente Reihe, f rus. расходящийся ряд, m pranc. série divergente, f … Fizikos terminų žodynas
Ряд Фурье — Добавление членов ряда Фурье … Википедия
Ряд в математике — Содержание. 1) Определение. 2) Число, определяемое рядом. 3) Сходимость и расходимость рядов. 4) Условная и абсолютная сходимость. 5) Равномерная сходимость. 6) Разложение функций в ряды. 1. Определения. Р. есть последовательность элементов,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ряд, в математике — Содержание. 1) Определение. 2) Число, определяемое рядом. 3) Сходимость и расходимость рядов. 4) Условная и абсолютная сходимость. 5) Равномерная сходимость. 6) Разложение функций в ряды. 1. Определения. Р. есть последовательность элементов,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ряд — I бесконечная сумма, например вида u1 + u2 + u3 +. + un +. или, короче, Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей… … Большая советская энциклопедия
РЯД — б е с к о н е ч н а я с у м м а, последовательность элементов (наз. ч л е н а м и д а н н о г о р я д а) нек рого линейного топологич. пространства и определенное бесконечное множество их конечных сумм (наз. ч а с т и ч н ы м и с у м м а м и р я… … Математическая энциклопедия
Что такое расходящиеся ряды
IX .1. Исследование рядов на сходимость
Числовым рядом (или просто рядом) называется бесконечная сумма ви да
где 
Если известен общий член ряда как функция его номера n : un = f ( n ), то ряд считают заданным.
Рассмотрим последовательность частичных сумм ряда (9.1):
Сформулируем некоторые свойства числовых рядов.
3. Если к ряду (9.1) прибавить или отбросить конечное число членов, то полученный ряд и ряд (9.1) сходятся или расходятся одновременно.
Следствие (достаточное условие расходимости ряда). Если 
Решение. Вычислим предел общего члена ряда:
Во многих случаях на вопрос о сходимости или расходимости числового ряда можно ответить с помощью достаточных признаков.
Сходимость или расходимость знакоположительного ряда часто устанавливается путем сравнения его с другим рядом, о котором известно, сходится он или не т. Подобное сравнение базируется на теоремах 9.2 и 9.3.
Теорема 9.2 (признак сравнения числовых знакоположительных рядов). Пусть даны два знакоположительных ряда
В этом случае ряд (9.4) называется минорантным, а ряд (9.5) – мажорантным рядом.
Теорема 9.3. (признак сравнения в предельной форме)
Примечание. Если l =1, то ряд (9.1) может быть как сходящимся, так и расходящимся
Признак Даламбера целесообразно применять, когда общий член ряда содержит факториалы и показательные выражения.
Теорема 9.5 (радикальный признак Коши). Если для ряда (9.1) с положительными членами существует конечный или бесконечный предел 
Решение. Учитывая теорему 9.5 и второй замечательный предел (3.13), вычисляем:
Теорема 9.6 (интегральный признак Коши). Если члены знакоположительного числового ряда 


Так как несобственный интеграл от общего члена ряда сходится, то и исходный ряд также сходится (согласно теореме 9.6)
Особое значение в теории числовых рядов (в частности, при их сравнении) имеет обобщенный гармонический ряд
где p > 0 – действительное число. Для исследования ряда (9.6) применим теорему 9.6 (интегральный признак Коши).
Помимо знакоположительных числовых рядов существует важный класс знакопеременных рядов, в которых члены ряда имеют произвольные знаки.
Теорема 9.7 (общий достаточный признак сходимости). Пусть дан знакопеременный ряд
составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (9.7)
Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Сформулируем основные свойства абсолютно сходящихся рядов.
2. Абсолютно сходящиеся ряды с суммами S 1 и S 2 можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна S 1 + S 2 ( S 1 – S 2 ).
Примечание. В случае условно сходящихся рядов подобные свойства, вообще говоря, места не имеют.
Используя указанные свойства, математические действия и операции производят только над абсолютно сходящимися рядами. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.
Частным случаем знакопеременных рядов являются знакочередующиеся ряды, члены которых имеют строго чередующиеся знаки:
Для знакочередующихся рядов имеет место следующий достаточный признак сходимости.
Ряд, членами которого являются функции от переменной x, называется функциональным:
В области сходимости функционального ряда его сумма является некоторой функцией от x : S = S ( x ), которая определяется равенством:
Частным случаем функционального ряда является степенной ряд, члены которого представляют собой степенные функции аргумента x:
Действительные (или комплексные) числа 

где x 0 – некоторое постоянное число.
Рассмотрим вопрос о нахождении области сходимости степенного ряда.
На практике радиус сходимости степенного ряда (9.11) отыскивают с помощью признака Даламбера. Для этого составляют ряд из модулей членов ряда:

С помощью радикального признака Коши (теоремы 9.5) можно показать, что радиус сходимости также вычисляется по формуле:
Примечание. Интервал сходимости степенного ряда (9.12) находят из неравенства | x – x 0 | R ; он имеет вид ( x 0 – R ; x 0 + R )
Следовательно, данный ряд абсолютно сходится в единственной точке х = 0.
Для нахождения области сходимости ряда применим признак Даламбера:
Данный ряд сходится абсолютно при тех значениях x , которые удовлетворяют неравенству
Исследуем сходимость ряда на концах полученного интервала.
Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при 
Таким образом, 
Что такое расходящиеся ряды
Числовым рядом (или просто рядом) называется бесконечная сумма ви да
где 
Если известен общий член ряда как функция его номера n : un = f ( n ), то ряд считают заданным.
Рассмотрим последовательность частичных сумм ряда (9.1):
Сформулируем некоторые свойства числовых рядов.
3. Если к ряду (9.1) прибавить или отбросить конечное число членов, то полученный ряд и ряд (9.1) сходятся или расходятся одновременно.
Следствие (достаточное условие расходимости ряда). Если 
Решение. Вычислим предел общего члена ряда:
Во многих случаях на вопрос о сходимости или расходимости числового ряда можно ответить с помощью достаточных признаков.
Сходимость или расходимость знакоположительного ряда часто устанавливается путем сравнения его с другим рядом, о котором известно, сходится он или не т. Подобное сравнение базируется на теоремах 9.2 и 9.3.
Теорема 9.2 (признак сравнения числовых знакоположительных рядов). Пусть даны два знакоположительных ряда
В этом случае ряд (9.4) называется минорантным, а ряд (9.5) – мажорантным рядом.
Теорема 9.3. (признак сравнения в предельной форме)
Примечание. Если l =1, то ряд (9.1) может быть как сходящимся, так и расходящимся
Признак Даламбера целесообразно применять, когда общий член ряда содержит факториалы и показательные выражения.
Теорема 9.5 (радикальный признак Коши). Если для ряда (9.1) с положительными членами существует конечный или бесконечный предел 
Решение. Учитывая теорему 9.5 и второй замечательный предел (3.13), вычисляем:
Теорема 9.6 (интегральный признак Коши). Если члены знакоположительного числового ряда 


Так как несобственный интеграл от общего члена ряда сходится, то и исходный ряд также сходится (согласно теореме 9.6)
Особое значение в теории числовых рядов (в частности, при их сравнении) имеет обобщенный гармонический ряд
где p > 0 – действительное число. Для исследования ряда (9.6) применим теорему 9.6 (интегральный признак Коши).
Помимо знакоположительных числовых рядов существует важный класс знакопеременных рядов, в которых члены ряда имеют произвольные знаки.
Теорема 9.7 (общий достаточный признак сходимости). Пусть дан знакопеременный ряд
составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (9.7)
Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Сформулируем основные свойства абсолютно сходящихся рядов.
2. Абсолютно сходящиеся ряды с суммами S 1 и S 2 можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна S 1 + S 2 ( S 1 – S 2 ).
Примечание. В случае условно сходящихся рядов подобные свойства, вообще говоря, места не имеют.
Используя указанные свойства, математические действия и операции производят только над абсолютно сходящимися рядами. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.
Частным случаем знакопеременных рядов являются знакочередующиеся ряды, члены которых имеют строго чередующиеся знаки:
Для знакочередующихся рядов имеет место следующий достаточный признак сходимости.
Ряд, членами которого являются функции от переменной x, называется функциональным:
В области сходимости функционального ряда его сумма является некоторой функцией от x : S = S ( x ), которая определяется равенством:
Частным случаем функционального ряда является степенной ряд, члены которого представляют собой степенные функции аргумента x:
Действительные (или комплексные) числа 

где x 0 – некоторое постоянное число.
Рассмотрим вопрос о нахождении области сходимости степенного ряда.
На практике радиус сходимости степенного ряда (9.11) отыскивают с помощью признака Даламбера. Для этого составляют ряд из модулей членов ряда:

С помощью радикального признака Коши (теоремы 9.5) можно показать, что радиус сходимости также вычисляется по формуле:
Примечание. Интервал сходимости степенного ряда (9.12) находят из неравенства | x – x 0 | R ; он имеет вид ( x 0 – R ; x 0 + R )
Следовательно, данный ряд абсолютно сходится в единственной точке х = 0.
Для нахождения области сходимости ряда применим признак Даламбера:
Данный ряд сходится абсолютно при тех значениях x , которые удовлетворяют неравенству
Исследуем сходимость ряда на концах полученного интервала.
Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при 
Таким образом, 
Расходящийся ряд
Смотреть что такое «Расходящийся ряд» в других словарях:
расходящийся ряд — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN divergent series … Справочник технического переводчика
расходящийся ряд — diverguojančioji eilutė statusas T sritis fizika atitikmenys: angl. divergent series vok. divergente Reihe, f rus. расходящийся ряд, m pranc. série divergente, f … Fizikos terminų žodynas
РАСХОДЯЩИЙСЯ РЯД — ряд, у к рого последовательность частичных сумм не имеет конечного предела. Напр., ряды расходятся. Р. р. стали появляться в работах математиков 17 18 вв. Л. Эйлер (L. Euler) первым пришел к выводу, что нужно ставить вопрос, не чему равна сумма,… … Математическая энциклопедия
Ряд Фурье — Добавление членов ряда Фурье … Википедия
Ряд в математике — Содержание. 1) Определение. 2) Число, определяемое рядом. 3) Сходимость и расходимость рядов. 4) Условная и абсолютная сходимость. 5) Равномерная сходимость. 6) Разложение функций в ряды. 1. Определения. Р. есть последовательность элементов,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ряд, в математике — Содержание. 1) Определение. 2) Число, определяемое рядом. 3) Сходимость и расходимость рядов. 4) Условная и абсолютная сходимость. 5) Равномерная сходимость. 6) Разложение функций в ряды. 1. Определения. Р. есть последовательность элементов,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ряд — I бесконечная сумма, например вида u1 + u2 + u3 +. + un +. или, короче, Одним из простейших примеров Р., встречающихся уже в элементарной математике, является сумма бесконечно убывающей… … Большая советская энциклопедия
РЯД — б е с к о н е ч н а я с у м м а, последовательность элементов (наз. ч л е н а м и д а н н о г о р я д а) нек рого линейного топологич. пространства и определенное бесконечное множество их конечных сумм (наз. ч а с т и ч н ы м и с у м м а м и р я… … Математическая энциклопедия




