Что такое распилы в математике
Факультативное занятие по математике 5 класс Составила: Геда Нат « Решение логических задач, задач на разрезание и распилы, арифметические ребусы. Подготовка к школьной олимпиаде.
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Факультативное занятие по математике 5 класс
В последние годы проводится много различных математических олимпиад. Кроме традиционных олимпиад, проводятся также дистанционные, устные, заочные, нестандартные и другие виды олимпиад. Математические олимпиады не только дают ценные материалы для суждения о степени математической подготовленности учащихся и выявляют наиболее одаренных и подготовленных молодых людей в области математики, но и стимулируют углубленное изучение предмета. Основная цель школьных олимпиад – это выявление талантливых ребят, развитие творческих способностей и интереса к научно-исследовательской деятельности у обучающихся.Создание необходимых условий для поддержки одаренных детей и распространение научных знаний среди молодежи.
Олимпиады готовят учащихся к жизни в современных условиях, в условиях конкуренции. Победы учащихся на олимпиадах международного и всероссийского уровней являются достаточным основанием для зачисления в вуз на льготных условиях.
Как добиться успешного участия школьника в математической олимпиаде? К ней надо серьёзно готовиться. Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. (Д.Пойа.)
Некоторые мои направления работы по подготовке учащихся к олимпиадам.
На уроке всегда можно найти место задачам, развивающим ученика, причем в любом классе, по любой теме. В пятом классе при изучении темы «Натуральные числа» можно предложить много разнообразных заданий, например:
Как, используя цифру 5 пять раз, знаки арифметических действий и скобки, выразить все натуральные числа от 0 до 10 включительно?
В шестом классе при изучении темы «Нахождение дроби от числа» следующие типы задач:
Некоторый товар стоил 500 рублей. Затем цену на него увеличили на 10%, а затем уменьшили на 10%. Какова стала цена в итоге?
При изучении темы » Степень с натуральным показателем» в седьмом классе предложить такие:
И таких примеров можно привести большое количество. Методической литературы для подборки заданий достаточно. Опыт мой и моих коллег показывает, большие трудности у учеников вызывают геометрические задачи. Хотя именно геометрия прекрасно развивает нестандартное мышление и выделяет людей способных заниматься математикой. Данный тип олимпиадных задач является самым обширным. Это задачи на разрезание, на построение, на нахождение углов; задачи, решение которых содержит идею, связанную с дополнительным построением.
Для развития интереса к решению нестандартных задач по математике в программу урочных занятий включаю рассмотрение занимательных задач, ребусов, задач-шуток, анаграмм и криптограмм, софизмов, задач прикладного характера.
Ученики активно принимают участие в заочных олимпиадах, которые дают импульс к саморазвитию и творческому поиску, в котором рождается подлинный интерес к науке и познанию. Участие в таком конкурсе способствует расширению кругозора и интеллектуальному росту учащихся, помогает профессиональному самоопределению старшеклассников.
Факультативное занятие по математике 5 класс
Тема: « Решение логических задач, задач на разрезание и распилы, арифметические ребусы. Подготовка к школьной олимпиаде.
Цель: В ооружить школьников дополнительными знаниями по олимпиадной математике, развить мышление и их математические способности. Развить познавательный интерес, творческое отношение к делу, стремление к самостоятельному приобретению знаний и умений, и применению их в своей практической деятельности.
Оказать педагогическую поддержку талантливым учащимся.
Научить использовать эвристические приемы поиска решения нестандартных задач.
Способствовать развитию логического мышления в ходе мыслительной деятельности: умение анализировать, сравнивать, синтезировать, обобщать, выделять главное, доказывать и опровергать;
Воспитание трудолюбия и самостоятельности.
План факультативного занятия:
Математическая разминка (8 мин).
Два сына и два отца съели три яйца. Поскольку яиц съел каждый?
Несла мать в корзиночке пять яблок. С ней были ее дети. Мать говорит детям: «Вас пять человек. Разделите эти яблоки между собой так, чтобы каждый получил по целому яблоку и одно яблоко осталось в корзине. Дети оказались догадливыми. Они разделили яблоки так, как потребовала мать. Как они это сделали?
У меня сестер и братьев поровну. А у моей сестры вдвое меньше сестер, чем братьев. Сколько нас?
Историческая справка (2 мин.):
Основная часть (20 мин.)
Метод решения задач на разрезания и распилы.
Количество кусков при разрезании на одно больше количества пилов и разрезов.
Количество пилов на одно меньше числа кусков.
Число кусков при разрезании «тортов» или «бубликов» через их центр в 2 раза больше числа резов. Следует уточнить, проходят ли все резы через 1 точку.
Забор длиной 16 метров укрепили столбами через каждые 2 метра. Сколько столбов понадобится для укрепления забора?
Бревно длиной 8 метров распилили на 8 равных частей. Сколько распилов сделали?
Веревку длиной 25 метров разрезали 5 раз. Сколько из нее получилось веревочек?
Квадрат содержит 16 клеток. Разделите квадрат на две равные части так, чтобы линия разреза шла по сторонам клеток. (Способы разрезания квадрата на две части будем считать различными, если части квадрата, полученные при одном способе разрезания, не равны частям, полученным при другом способе.)
Сколько всего решений имеет задача?
Прямоугольник 3 x 5 содержит 15 клеточек и центральная клетка удалена. Найдите пять способов разрезания оставшейся фигуры на две равные части так, чтобы линия разреза шла по сторонам клеток.
Игра «Супермыслитель » ( 12 мин)
Учащиеся делятся на две команды, нужно быстро и правильно решить задачу или разгадать ребусы. Оценивается данный вид деятельности по быстроте, количеству и качеству выданных правильных ответов.
Капитаны команд в порядке очереди вытаскивают ребусы и две команды приступают к разгадке заданий на время.
Лягушка находится на дне колодца глубиной 60 м. За день она поднимается на 18 м, а потом спускается на 17 м и остается на месте до следующего дня. На следующий день лягушка проделывает снова такой же маршрут. Через сколько дней лягушка выйдет из колодца?
Задание 2 Разгадать ребусы 1,2,3, 4
Прямоугольник 4 x 9 клеток разрежьте по сторонам клеток на две равные части так, чтобы из них затем можно было сложить квадрат.
Подведение итогов игры.
Домашнее задание: составить небольшой кроссворд на тему: « задачи на разрезание и распилы» (1 мин.).
Рефлексия и подведение итогов (2 минуты)
Учащиеся поднимают нужную картинку,, которая лежит на парте и учитель видит общую картину происходящего.
Методы решения задач на распиливание и разрезание
Чтобы понять, о чём именно речь, в качестве примера приведём задачу:
Есть несколько полосок бумаги. После того, как некоторое количество из них разрезали на куски, получили 14 кусочков (возможно, вместе с нетронутыми полосками). Сколько полосок бумаги было первоначально, если всего произвели 6 разрезов?
Прежде, чем решать эту задачу, рассмотрим другой случай. Пусть у нас есть есть доски, на которых в сумме делают 4 распила.
Мы можем сделать вывод, что число получившихся кусков равно числу досок + число распилов. В данном случае нераспиленную доску мы принимаем за 1 кусок. Это верно не только для 4-х распилов, но и для любого другого числа. Можете самостоятельно проверить сами.
Причём эта формула не зависит от того, как именно пилят/режут на части.
Пример: Пусть у нас есть три доски, которые разным образом делят на 4 части.
Вне зависимости от того, как мы пилим доски, формула
Число распиливаемых объектов (разрезаемых) + число распилов (разрезов) = число получившихся кусков
остаётся верной. Нераспиленную доску мы принимаем за один кусок.
Количество частей, получившихся после разрезания или распиливания одного объекта всегда на один больше, чем количество распилов.
Решение задачи из начала этого урока
Напомним её условие:
Есть несколько полосок бумаги. После того, как некоторое количество из них разрезали на куски, получили 14 кусочков (возможно, вместе с нетронутыми полосками). Сколько полосок бумаги было первоначально, если всего произвели 6 разрезов?
x – первоначальное количество полосок бумаги
Упражнение «Задачи на разрезы и распилы»
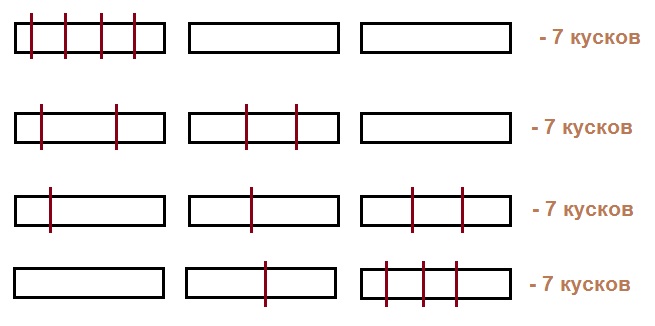
Учитель предлагает учащимся выполнить практическую работу. Каждый ученик получает полоску бумаги, на которой указано, сколько разрезов надо выполнить, разбивая полоску на части. Затем учитель предлагает учащимся определить, сколько частей получилось после выполнения всех разрезов, и сделать вывод о зависимости числа частей от количества выполненных разрезов: число частей на единицу больше, чем число разрезов.
После этого учитель читает условия задач, а учащиеся с помощью сигнального блокнота (веера чисел) показывают ответы.
Можно предложить учащимся решить следующие задачи (количество и содержание задач – по усмотрению учителя; в скобках приведены ответы для учителя).
– Сделали 5 разрезов. Сколько получилось частей? (6 частей)
– Веревку разрезали на 5 частей. Сколько сделали разрезов? (4 разреза)
– На бревне сделали 8 зарубок. На сколько частей распилят бревно? (на 9 частей)
– Сколько зарубок надо сделать, чтобы распилить бревно на 4 части? (3 зарубки)
– Два ленты разрезали на 3 части каждую. Сколько всего разрезов было сделано? (4 разреза)
– Распилили 10 бревен, каждое – пополам. Сколько всего распилов было сделано? (10 распилов)
– Несколько листов бумаги разрезали на три части каждый. Оказалось, что всего было сделано 12 разрезов. Сколько листов бумаги было разрезано? (6 листов)
В зависимости от уровня математической подготовки учащихся можно предложить несколько задач повышенной сложности.
— За 3 минуты бревно распилили на полуметровые поленья. Каждый распил выполнялся за одну минуту. Какой длины было бревно? (4 метра).
— За 8 минут 2 одинаковых бревна распилили на полуметровые поленья. Каждый распил выполнялся за одну минуту. Какой длины было каждое бревно? (5 метров).
— Имеются бревна одинаковой толщины длиной 4 м и 5 м. Бревно можно отпилить за 1 минуту. Как быстрее напилить 20 поленьев длиной по 1 метру – распиливать четырехметровые или пятиметровые бревна? (Ответ: четырехметровые: из одного четырехметрового бревна за 3 минуты получается 4 полена, значит, 20 поленьев за 15 минут; из одного пятиметрового бревна за 4 минуты получается 5 поленьев, т.е. 20 поленьев за 16 минут).
Подведение итогов
Учитель предлагает учащимся ответить, решение каких задач на разрезания и распилы вызвало наибольший интерес.
 | ЗАНЯТИЕ 25 ПРИЁМЫ МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ПРОСТЫХ ЗАДАЧ НА ВЗВЕШИВАНИЕ |
| Краткое содержание:содержание занятия направлено на совершенствование умения решать простые задачи на взвешивание, на развитие навыков моделирования при решении простых задач на взвешивание. Примечание: Примечание: для проведения занятия нужны рычажные лабораторные весы (без гирь), 11 «настоящих» монет равные по массе и 1 «фальшивая» монета меньшей массы; 7-10 кругов желтого цвета, 4-6 кругов белого цвета. |
Методические рекомендации
Разминка
Учитель кратко пересказывает сюжет венгерской народной сказки «Два жадных медвежонка» и предлагает учащимся придумать способ, как разделить головку сыра на две равные по массе части:
а) если у медвежат есть весы с гирями или электронные весы;
б) если у медвежат есть весы рычажные (равновесы, «уточки»), но без гирь;
в) если у медвежат нет весов.
После обсуждения полезно назвать слова, которые характеризуют Лису (хитрая, обманщица, плутовка, мошенница) и объяснить, почему в сказке Лиса так описывается в сказке.
Задачи на промежутки
Урок 7. Математика и игры 3–4 классы
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Задачи на промежутки»
Сегодня наше занятие будет посвящено задачам на промежутки, для решения которых надо уметь наглядно представить то, о чём говорится в задаче. При этом вычислений для решения таких задач почти не требуется.
Давайте рассмотрим несколько задач.
Задача первая. Зайцу надо разделить бревно на 4 части. Сколько для этого ему придётся сделать распилов?
Получается, что зайцу придётся сделать 3 распила, чтобы разделить бревно на 4 части.
Вторая задача. Саше надо разделить бублик на 4 части. Сколько для этого ему надо сделать разрезов?
Чтобы разделить бублик на 4 части, Саше надо сделать 4 разреза.
Получается, что бублик разделили на 4 части, сделав 4 разреза, а бревно разделили на 3 части, сделав только 3 разреза.
И теперь мы можем сделать вывод, что при делении на части предмета, похожего на незамкнутую линию (как, например, бревно), число разрезов будет на один меньше, чем число частей, на которое этот предмет надо разделить. А вот при делении круглого предмета (или любого предмета, похожего на замкнутую кривую или замкнутую ломаную линию) на несколько частей, необходимо сделать столько разрезов, на сколько частей надо разделить этот предмет.
То есть при делении на части любых предметов, кроме похожих на замкнутые кривые и ломаные, количество разрезов на один меньше, чем количество полученных частей предмета.
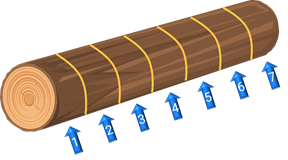
Задача третья. Заяц распилил бревно на 7 частей. Сколько для этого он сделал распилов?
Решение. Сразу обратим внимание на то, что заяц делил на части бревно, а не какой-то круглый предмет. Поэтому число распилов на один меньше, чем число частей.
В условии задачи сказано, что заяц распилил бревно на 7 частей, а значит, он сделал 7 минус 1, то есть 6 распилов.
Давайте убедимся в этом. Распилим бревно на семь частей.
Действительно, сделав 6 распилов, мы разделили бревно на 7 частей.
Задача четвёртая. Катя разрезала ленту длиной 12 м на равные куски. Длина каждого куска равна 2 м. Сколько девочка сделала разрезов?
Решение. Чтобы решить эту задачу, в первую очередь надо узнать, на сколько кусков Катя разрезала ленту. Для этого надо длину всей ленты, то есть 12 м, разделить на длину каждого куска, то есть на 2. Это равно 6.
12 : 2 = 6 (к.) – число кусков
Получается, что Катя разрезала ленту на шесть кусков.
Вы уже знаете, что в данном случае разрезов будет на один меньше, чем кусков. Это потому что лента похожа на незамкнутую линию.
Итак, мы выяснили, что Катя разрезала ленту на 6 кусков, а значит она сделала 6 минус 1, то есть 5 разрезов.
6 – 1 = 5 (р.) – число разрезов
Прежде чем записать ответ, давайте в этом убедимся.
Действительно, сделав 5 разрезов, разделили ленту на 6 кусков.
Задача пятая. Требуется распились доску на 10 частей. Каждый распил занимает 3 мин. Сколько времени потребуется на эту работу?
Решение. Прежде чем ответить на вопрос задачи, необходимо выяснить, сколько надо сделать распилов, чтобы разделить доску на 10 частей.
Число распилов будет на один меньше, чем число частей, на которое надо распилить доску. А так как частей должно получиться 10, то распилов будет 10 минус 1, то есть 9.
10 – 1 = 9 (р.) – число распилов
Можно убедиться в этом, делая распилы.
В условии задачи сказано, что один распил занимает 3 минуты. Всего должно быть сделано 9 распилов. Поэтому, чтобы найти время, которое понадобится для распиливания доски на 10 частей, надо 3 умножить на 9, а это равно 27. То есть 27 минут потребуется, чтобы распилить доску на 10 частей.
3 · 9 = 27 (мин) – время, которое потребуется на работу
Теперь решим такую задачу. Вдоль дорожки, длина которой 18 м, решили посадить тюльпаны через каждые 2 м. Причём тюльпаны надо посадить и в начале, и в конце дорожки. Сколько тюльпанов понадобится?
Решение. Итак, тюльпаны будут располагаться на расстоянии 2 метров друг от друга. Разделим 18 на 2. Получим 9. То есть 9 двухметровых промежутков будет между посаженными тюльпанами.
Можно подумать, что тюльпанов будет на один меньше, чем двухметровых промежутков между ними, то есть 8.
А вот и нет! Посмотрите на рисунок.
Так как тюльпаны надо посадить и на концах дорожки, то их будет на один больше, чем промежутков между ними. То есть понадобится 10 тюльпанов.
Ответ: 10 тюльпанов.
Таким образом, можно сделать вывод, что при делении на части какого-то предмета по длине, точек, делящих его на части, всегда на одну меньше, чем частей. Это как в задачах про распиливание брёвен и доски, а также про разрезание ленты. Но если нам нужны и крайние точки этого предмета, как в задаче про тюльпаны, то точек будет на одну больше, чем частей.