Что такое распределение максвелла

Что такое распределение максвелла

Пусть имеется n тождественных молекул, находящихся в состоянии беспорядочного теплового движения при определенной температуре. После каждого акта столкновения между молекулами, их скорости меняются случайным образом. В результате невообразимо большого числа столкновений устанавливается стационарное равновесное состояние, когда число молекул в заданном интервале скоростей сохраняется постоянным.

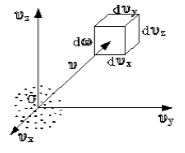
В результате каждого столкновения проекции скорости молекулы испытывают случайное изменение на Δυ_x, Δυ_y, Δυ_z, причем изменения каждой проекции скорости независимы друг от друга. Будем предполагать, что силовые поля на частицы не действуют. Найдем в этих условиях, каково число частиц dn из общего числа n имеет скорость в интервале от υ до υ+Δυ. При этом мы не можем ничего определенного сказать о точном значении скорости той или иной частицы υ_i, поскольку за столкновениями и движениями каждой из молекул невозможно проследить ни в опыте, ни в теории. Такая детальная информация вряд ли имела бы практическую ценность.

Распределение молекул идеального газа по скоростям впервые было получено знаменитым английским ученым Дж. Максвеллом в 1860 году с помощью методов теории вероятностей.

Максвелл Джеймс Клерк (1831 – 1879) – английский физик. Работы посвящены электродинамике, молекулярной физике, общей статике, оптике, механике, теории упругости. Установил статистический закон, описывающий распределение молекул газа по скоростям. Самым большим достижением Максвелла является теория электромагнитного поля, которую он сформулировал в виде системы нескольких уравнений, выражающих все основные закономерности электромагнитных явлений.

Скорость – векторная величина. Для проекции скорости на ось х (x-й составляющей скорости) из (2.2.1) имеем

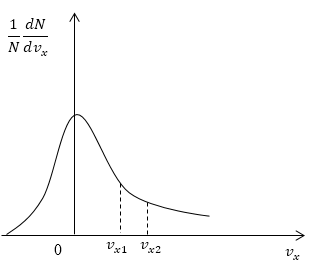
Графическое изображение функции показано на рисунке 2.2. Видно, что доля молекул со скоростью не равна нулю. При , (в этом физический смысл постоянной А1).

Эта величина (dn_xyz) не может зависеть от направления вектора скорости . Поэтому надо получить функцию распределения молекул по скоростям независимо от их направления, то есть по абсолютному значению скорости.

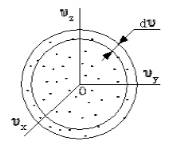
Если собрать вместе все молекулы в единице объёма, скорости которых заключены в интервале от υ до υ+dυ по всем направлениям, и выпустить их, то они окажутся через одну секунду в шаровом слое толщиной dυ и радиусом υ (рис. 2.4). Этот шаровой слой складывается из тех параллелепипедов, о которых говорилось выше.

При dυ = 1 получаем плотность вероятности, или функцию распределения молекул по скоростям:

Обозначим: тогда из (2.3.4) получим:

Рассмотрим пределы применимости классического описания распределения частиц по скоростям. Для этого воспользуемся соотношением неопределенностей Гейзенберга. Согласно этому соотношению координаты и импульс частицы не могут одновременно иметь определенное значение. Классическое описание возможно, если выполнены условия:

Здесь – постоянная Планка – фундаментальная константа, определяющая масштаб квантовых (микроскопических) процессов.

Таким образом, если частица находится в объеме , то в этом случае возможно описание ее движения на основе законов классической механики.

Наиболее вероятная, среднеквадратичная и средняя арифметическая скорости молекул газа

Рассмотрим, как изменяется с абсолютной величиной скорости число частиц, приходящихся на единичный интервал скоростей, при единичной концентрации частиц.

График функции распределения Максвелла

Величину скорости, на которую приходится максимум зависимости , называют наиболее вероятной скоростью.

Найдем эту скорость из условия равенства производной .

Для одного моля газа:

Формула Максвелла для относительных скоростей

Для решения многих задач удобно использовать формулу Максвелла, где скорость выражена в относительных единицах.

Относительную скорость обозначим через u:

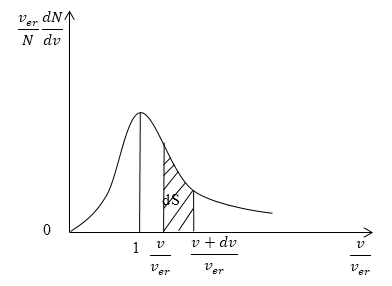
На рисунке 2.7 показано максвелловское распределение частиц f(υ), имеющих скорости от υ до υ+dυ. За единицу скорости здесь взята наиболее вероятная скорость.

Полезно знать, что .

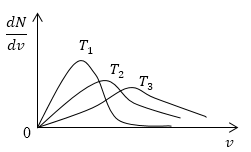
Зависимость функции распределения Максвелла от массы молекул и температуры газа

На рисунке 2.8 показана зависимость f(υ) при различных температурах и массах молекул газа.

Источник

Закон распределения молекул по скоростям

С помощью закона распределения молекул по скоростям мы можем описать, как именно в макроскопической системе происходит распределение частиц (при условии ее нахождения в термодинамическом равновесии). Такое распределение называется стационарным, и воздействия внешних сил на систему при этом не происходит.

Данный закон распространяется как на жидкости, так и на газы, если на них действуют законы классической механики. Если мы знаем, как именно распределяются молекулы по своим скоростям, значит, мы можем ответить, какой объем молекул имеет определенную скорость в условиях заданной температуры в равновесном состоянии.

Мы видим, что в декартовой системе координат здесь отмечены именно проекции скоростей, а не координаты. Тогда исходный вопрос можно переформулировать так: «Как именно будут распределяться молекулы в пространстве скоростей»?

Распределение Максвелла

Поскольку, как мы уже отмечали, газ находится в равновесном состоянии, то направления движений частиц являются равноправными. Значит, допустимо считать, что в пространстве скоростей распределение молекул является симметричным и имеет сферическую форму.

Таким образом, закон распределения молекул по модулям скоростей имеет следующий вид:

По проекциям скоростей распределение Максвелла может быть записано так:

Также возможен следующий вариант записи распределения Максвелла:

Здесь υ υ e r обозначает наиболее вероятную скорость движения молекулы.

Как выглядит распределение Максвелла на графике

Кривая распределения молекул по скоростям на графике выглядит так:

Скорости всех молекул принадлежат интервалу от нуля до плюс бесконечности, значит, будет верным равенство:

Оно называется условием нормировки функции распределения.

Следовательно, распределение Максвелла по скоростям имеет зависимость от температуры газа и массы его молекул. Объем и давление можно не учитывать.

Условие: вычислите, какова будет наиболее вероятная скорость молекул газа при температуре Т в равновесном состоянии.

Нам потребуется распределение Максвелла (распределение по модулям скоростей).

Максимум функции будет соответствовать самой вероятной скорости. Дифференциация выражения по скорости и сравнение ее с нулем даст нам следующий результат:

Возьмем формулу наиболее вероятной скорости из предыдущей задачи.

υ υ e r = 2 k T m 0

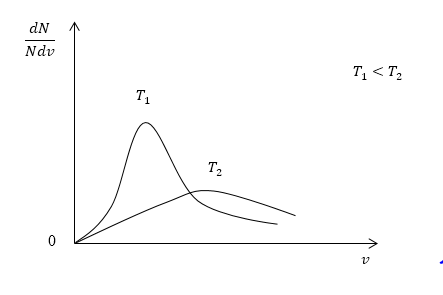
Понятно, что чем больше будет температура, тем выше будет скорость молекул, т.е. произойдет смещение максимума в сторону больших скоростей. Поскольку площадь под кривой распределения является постоянной величиной, кривые на графике будут показаны следующим образом:

Источник

Распределение Максвелла-Больцмана

Распределение (или закон) Максвелла—Больцмана описывает распределение молекул газа по координатам и скоростям при системном воздействии внешнего потенциального поля.

Это распределение выводится из распределения Гиббса ( 1 ) :

где W p – вероятность одного из состояний системы с энергией ε p (полная энергия, состоящая из кинетической и потенциальной, которая присуща частицам). Рассмотрим чаще всего используемые формы распределения Максвелла-Больцмана.

Формы распределения Максвелла-Больцмана

Формула распределения для концентрации частиц

Формула распределения для вероятности импульса и координаты

и распределение Больцмана:

Таким образом, распределения Максвелла и Больцмана служат составляющими элементами распределения Гиббса. Энергия молекул, движущихся в поле тяжести вверх, получает уменьшение, но в распределении Максвелла-Больцмана по скоростям средняя энергия при этом неизменна. Сохранность средней энергии частиц, когда происходит уменьшение энергии отдельно взятой молекулы, возможно благодаря выбыванию молекул с меньшей энергией из потока при увеличении высоты. Средняя энергия молекул, движущихся вниз, постоянна из-за присоединения к потоку молекул, выбывших из потока, направленного вверх.

Сходство между распределениями Максвелла и Больцмана

Рассмотрим практические задачи на распределение Максвелла-Больцмана.

Пусть задан некий газ, имеющий неизменную массу, переводимый из одного равновесного состояния в другое. Необходимо определить, происходит ли изменение в распределении молекул по скоростям: 1 ) положение максимума кривой в распределении Максвелла; 2 ) площадь под этой кривой?

Составим запись распределения Максвелла по модулю скорости:

При переводе газа из одного равновесного состояния в другое имеет место изменение температуры газа. Таким образом, положение максимума кривой Максвелла изменится.

При этом в случае, когда температура увеличивается, максимум получит сдвиг в сторону больших скоростей, а величина пика (высота по вертикальной оси) уменьшится (рисунок 1 ).

Заданный условием скоростной интервал невелик, т.е. допустимо применять теорему о среднем, и тогда:

Источник

Физика Б1.Б8.

Молекулярная физика и термодинамика

1. Введение

Основы молекулярной физики были заложены трудами Ломоносова, Джоуля, Больцмана, Клаузиуса, Максвелла и других ученых. Благодаря их трудам молекулярная физика прочно утвердилась в науке. Непосредственным опытным подтверждением молекулярно-кинетической теории являются процесс диффузии, броуновского движения, распространения запаха и многие другие явления.

Движение каждой молекулы в веществе может быть описано законами классической механики. Однако число молекул в веществе чрезвычайно велико, направления и величины скоростей молекул совершенно случайны и непрерывно изменяются так, что становится невозможным охватить уравнениями движения всю совокупность молекул и сделать какие-либо выводы об их поведении.

Тем не менее, состояние вещества и его изменение определяется заданием небольшого числа определенных параметров, как температура, давление, объем, плотность и т.д., значения которых невозможно указать на основе решений уравнений классической механики. Дело в том, что свойства огромного числа молекул подчиняется особым, статистическим закономерностям. Статистическая физика изучает статистические закономерности, описывающие поведение большой совокупности объектов. Она основывается на теории вероятностей и позволяет вычислять средние значения величин, характеризующих движение всей совокупности молекул (средние скорости молекул, средние кинетические энергии, средние значения импульса и т. д.) и на этой основе истолковывает свойства вещества, непосредственно наблюдаемые на опыте (давление, температура и т.д.). В этом состоит суть молекулярно-кинетического изучения вещества.

Наряду со статистическим, существует термодинамический метод изучения вещества. В отличие от статистического метода термодинамический метод не интересуется строением вещества. Термодинамика изучают условия превращения энергии и характеризует их с количественной стороны.

В основе термодинамики лежит небольшое число закономерностей, установленных на основе большого числа опытных фактов и получивших название начала термодинамики.

У статистической физики и термодинамики общий предмет изучения – свойства вещества и происходящие в нем процессы. Подходя к изучению этих свойств с разных точек зрения, эти методы взаимно дополняют друг друга.

Совокупность тел, могущих обмениваться энергией между собой и с внешними телами, не входящими в эту систему, называется термодинамической системой. Одним из основных понятий термодинамики является понятие состояния системы. Состояние системы определяется совокупностью значений всех величин, характеризующих физические свойства системы и называемых термодинамическими параметрами (температура, давление плотность, теплоемкость, электропроводность и т. д.). Состояние системы называется стационарным, если значения всех термодинамических параметров не изменяются во времени. Стационарное состояние называется равновесным, если его неизменность не обусловлена протеканием каких-либо процессов во внешних по отношению к данной системе телах.

Исследования показывают, что параметры состояния тел взаимно связаны и могут быть выражены друг через друга. Поэтому термодинамическое состояние задается только ограниченным числом параметров состояния. Такие параметры называются основными параметрами состояния. Важнейшими параметрами состояния химически однородных систем являются плотность, объем, давление, температура. И между этими параметрами существует связь, выражаемая в виде математического уравнения . Уравнение, связывающее основные параметры состояния, называется уравнением состояния системы.

Источник

Распределение Максвелла

Функция плотности распределения

Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы ). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

Содержание

Распределение Максвелла

Распределение по вектору импульса

В случае идеального газа, состоящего из не взаимодействующих атомов в основном состоянии, вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы следующим образом

,

Мы можем поэтому переписать уравнение (1) как:

,

константа нормировки c, может быть определена из того факта, что вероятность молекулы имеют какой-либо импульс должна быть равна единице. Поэтому интеграл уравнения (4) по всем значениям p_x, p_y, и p_z должен быть равен единице. Можно показать, что:

.

Таким образом, чтобы интеграл в уравнении (4) имел значение 1 необходимо, чтобы

.

Подставляя выражение (6) в уравнение (4) и используя тот факт, что p_i = mv_i, мы получим

.

Распределение по вектору скорости

Учитывая, что плотность распределения по скоростям f_v пропорциональна плотности распределения по импульсам:

и используюя p = mv мы получим:

,

что является распределением Максвелла по скоростям. Вероятность обнаружения частицы в бесконечно малом элементе [dv_x, dv_y, dv_z] около скорости v = [v _x , v _y , v _z ] равна

Распределение по абсолютной величине импульса

Интегрируя, мы можем найти распределение по абсолютной величине импульса

Распределение по энергии

Наконец, используя соотношение p 2 = 2 mE мы получаем распределение по энергии:

Распределение по проекции скорости

Распределение Максвелла для вектора скорости [v_x, v_y, v_z] — является произведением распределений для каждого из трех направлений:

,

где распределение по одному направлению:

Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю.

Распределение по модулю скоростей

Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, v определяется как:

поэтому модуль скорости всегда будет больше или равен нулю. Так как все v_i распределенны нормально, то v 2 будет иметь хи-квадрат распределение с тремя степенями свободы. Если f(v) — функция плотности вероятности для модуля скорости, то:

,

таким образом, функция плотности вероятности для модуля скорости равна

Характерная скорость

Хотя Уравнение (11) дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость, часто более интересны другие величины, такие как средние скорости частиц. В следующих подразделах мы определим и получим наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость.

Наиболее вероятная скорость

наиболее вероятная скорость, v_p — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению f(v). Чтобы найти её, необходимо вычислить df/dv, приравнять её нулю и решить относительно v:

Средняя скорость

Подставляя f(v) и интегрируя, мы получим

См. также

he:התפלגות מקסוול בולצמן nl:Maxwell-Boltzmann-verdeling pl:Rozkład Maxwella-Boltzmanna sl:Boltzmannova porazdelitev uk:Распределение Максвелла

Источник