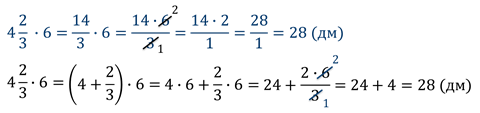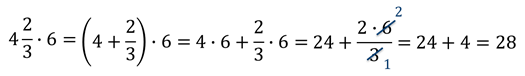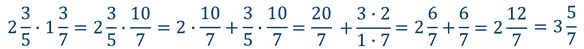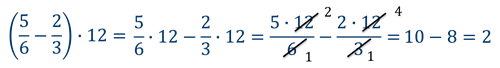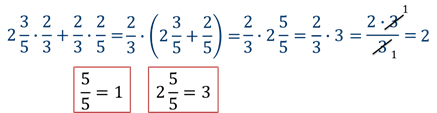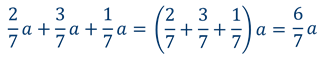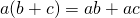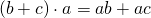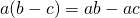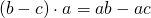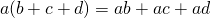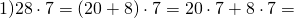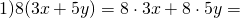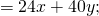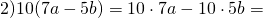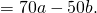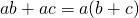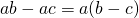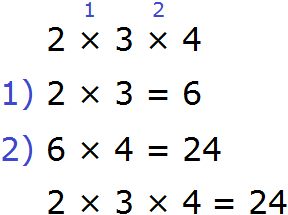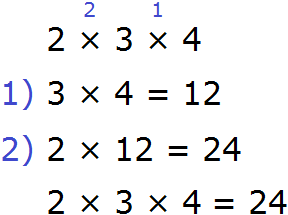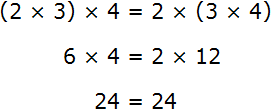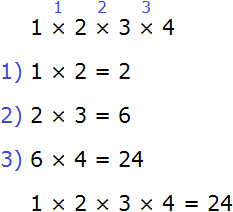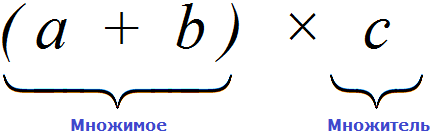Что такое распределительное свойство умножения 7 класс

Применение распределительного свойства умножения

Урок 15. Математика 6 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Применение распределительного свойства умножения»

Сегодня на уроке мы вспомним уже известное вам распределительное свойство умножения и применим его при решении задач и примеров.

Для начала давайте вспомним распределительное свойство умножения относительно сложения и относительно вычитания и запишем их в буквенном виде.

Итак, распределительное свойство умножения относительно сложения гласит, что для того чтобы умножить сумму на число, можно умножить на это число

каждое слагаемое и сложить получившиеся произведения.

Распределительное свойство умножения относительно вычитания говорит, что

для того чтобы умножить разность на число, можно умножить на это число

уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Также мы с вами знаем, что с помощью распределительного свойства очень удобно упрощать выражения. А ещё мы помним, что распределительное свойство позволяет раскрывать скобки и выносить общий множитель за скобки.

Итак, мы вооружились знаниями распределительного свойства умножения, а значит, теперь можем приступить к изучению новой темы.

Муравей за одну минуту пробегает 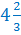дм. Какое расстояние пробежит муравей за 6 минут?

Но смотрите, эту задачу можно решить проще. Мы помним, что смешанное число это сумма целой и дробной части, значит, смешанное число можно записать в виде суммы. Что мы сейчас и сделаем.

Мы применили распределительное свойство умножения относительно сложения и упростили себе вычисления.

Чтобы умножить смешанное число на натуральное число, можно:

1) умножить целую часть на натуральное число;

2) умножить дробную часть на это натуральное число;

Помните, что всегда надо смотреть, как удобнее выполнять вычисления!

Правило умножения смешанных чисел:

Для того чтобы умножить смешанное число на смешанное число, можно:

1) перевести одно смешанное число в неправильную дробь;

2) умножить целую часть второго множителя на неправильную дробь;

3) умножить дробную часть второго множителя на неправильную дробь;

Найдите значение выражения:

Используя распределительное свойство умножения можно упрощать и буквенные выражения.

Итак, сегодня на уроке мы с помощью распределительного свойства умножения вывели правила умножения смешанных чисел.

Источник

Распределительное свойство умножения

Распределительное свойство умножения — важное правило, полезное в устном счете и при раскрытии скобок.

Распределительное свойство умножения относительно сложения:

Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.

С помощью букв распределительное свойство умножения относительно сложения записывают так:

Распределительное свойство умножения относительно вычитания:

Чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе.

С помощью букв распределительное свойство умножения относительно вычитания записывают так:

Распределительное свойство умножения верно и для большего количества чисел. Например, для трех слагаемых распределительное свойство умножения относительно сложения имеет вид:

Распределительное свойство умножения упрощает устный счет.

Этот пример можно решить также с помощью распределительного свойства умножения относительно вычитания:

С помощью распределительного свойства умножения можно раскрывать скобки.

(Более подробно тема раскрытия скобок рассматривается после изучения отрицательных чисел).

Распределительное свойство умножения можно применить и в обратном порядке:

Говорят: «Общий множитель a выносим за скобки. В скобках остается b плюс c».

Говорят: «Общий множитель a выносим за скобки. В скобках остается b минус c».

Более подробно вынесение общего множителя за скобки изучают в курсе алгебры 7 класса.

Источник

Свойства умножения и деления

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Свойства умножения

Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.

Узнаем, какие бывают свойства умножения и как их применять.

Переместительное свойство умножения

От перестановки мест множителей произведение не меняется.

То есть, для любых чисел a и b верно равенство: a * b = b * a.

Это свойство можно применять к произведениям, в которых больше двух множителей.

Сочетательное свойство умножения

Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.

То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).

Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.

Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.

То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.

Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.

В обратную сторону распределительное свойство умножения относительно сложения звучит так:

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.

То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.

В обратную сторону распределительное свойство умножения относительно вычитания звучит так:

Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.

Свойство единицы при умножении

Если умножить любое целое число на единицу, то в результате получится это же число.

То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?

Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.

Пример 2

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 3

Упростить выражение: 27a – 16a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Источник

Распределительное свойство умножения

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описание слайда:

Тема урока:
Распределительное свойство умножения

Описание слайда:

Задачи урока:
1.Выучить распределительное свойство умножения относительно сложения и относительно вычитания.
2.Научиться применять распределительное свойство умножения для упрощения выражений, при решении уравнений и текстовых задач.
3.Развивать наблюдательность, память.

Описание слайда:

Устные упражнения
72 * 4
15 * 7
61 * 6
44 * 5
24 * 3
130 * 4
124 * 3
288
105
366
220
72
520
372

Описание слайда:

Вычисли удобным способом
(2593 + 1389) – 1593

Описание слайда:

У П Р О С Т И
(125 + m) + 75

Описание слайда:

Задача.
1.Сколько всего ног у 15 котят и 15 цыплят?
15 * 4 + 15 * 2 =90 или (4 + 2) * 15 = 90
Вывод: 15*4+15*2 = (4+2)*15

2. На сколько ног у 15 котят больше, чем у 15 цыплят?
15 * 4 – 15 * 2 = 30 или (4 – 2) * 15 = 30
Вывод: 15*4- 15*2 = (4-2) *15

Описание слайда:

(а +в)  с = а  с +в  с распределительное свойство умножения относительно сложения
Правило:
чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения

Описание слайда:

распределительное свойство умножения относительно вычитания
Правило:
чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

Описание слайда:

Распределительное свойство умножения позволяет упрощать выражения

Описание слайда:

Распределительное свойство умножения позволяет раскрывать скобки

Описание слайда:

Описание слайда:

Распределительное свойство помогает решать уравнения
7x +41x =192 17x – 4x =195
48x =192 13x = 195
x = 192:48 x=195:13
x=4 x=15
630: (63x- 42x) +53 = 68
630:(21x) +53 =68
630:(21x)=68-53
630:(21x)=15
21x=630:15
21x=42
x=42:21
x=2

Описание слайда:

Распределительное свойство умножения применяют при решении задач
Задача.
Я задумала число. Если его увеличить на 20, а результат умножить на 6, то получится 150. какое число я задумала?
Пусть я задумала число X.
Составим уравнение: (X +20)*6=150
Решим его: 6Х + 120 =150
6Х = 150-120
6Х = 30
Х=30:6
Х = 5
Ответ. Задумано число 5.

Описание слайда:

Описание слайда:

Подведение итогов
1 Записать распределительное свойство умножения относительно сложения, используя буквы x, y, z.
2.Записать распределительное свойство умножения относительно вычитания,используя буквы x, y, z.

Описание слайда:

Тест. Упростить выражения

Описание слайда:

Описание слайда:

Домашнее задание
Прочитать п.14 и выучить правила

Решить упражнения
№595 а)б)
№596 а)в)
№600
№604

Описание слайда:

Презентация урока создана
учителем математики
ГОУ СОШ № 511

Гончаровой Валентиной Николаевной

с использованием материалов уроков «Упрощение выражений» учителей:
Слесарева В.Г., Салковой Н.А., Шмыр А.С.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс профессиональной переподготовки

Охрана труда

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Администрация Ростовской области Информационно-программная система работы многофункционального центра предоставления государс

СИСТЕМА КРЕДИТНОГО ИНФОРМИРОВАНИЯ: СРАВНИТЕЛЬНО-ПРАВОВОЙ АСПЕКТ

Общая информация Предназначение Преимущества и особенности Принципы работы Возможности Корпоративные решения Эффективность Час

Автоматизация общего анализа крови Гематологические анализаторы Diatron (Австрия)

Mirapolis Virtual Room

Функциональная стандартизация информационно-образовательной среды вуза

Net Languages ‘самая эффективная языковая школа в сети’ magistre.netlanguages.com

Лекция по экономике

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5378276 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Международный конгресс-выставка «Молодые профессионалы» пройдет с 12 по 14 декабря в Москве

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Во Франции планируют ввести уголовное наказание за буллинг в школе

Время чтения: 1 минута

МГУ откроет первую в России магистерскую программу по биоэтике

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Законы математики

В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.

У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.

Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.

В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.

Переместительный закон сложения

Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:

Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.

Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:

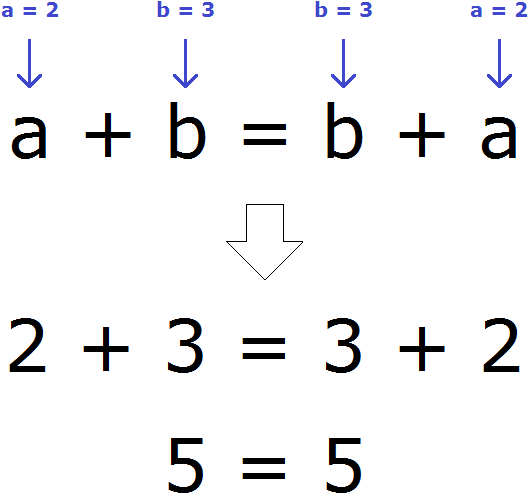
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:

Сочетательный закон сложения

Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.

Рассмотрим сумму из трёх слагаемых:

Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:

2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10

Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2

2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10

Видно, что в обоих случаях получается один и тот же результат.

Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(2 + 3) + 5 = 2 + (3 + 5)

Запишем сочетательный закон сложения с помощью переменных:

Переместительный закон умножения

Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.

В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:

5 × 2 = 2 × 5

Запишем переместительный закон умножения с помощью переменных:

Сочетательный закон умножения

Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

Рассмотрим следующее выражение:

Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:

Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2

Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

Запишем сочетательный закон умножения с помощью переменных:

a × b × с = (a × b) × с = a × (b × с)

Пример 2. Найти значение выражения 1 × 2 × 3 × 4

Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число или число на сумму.

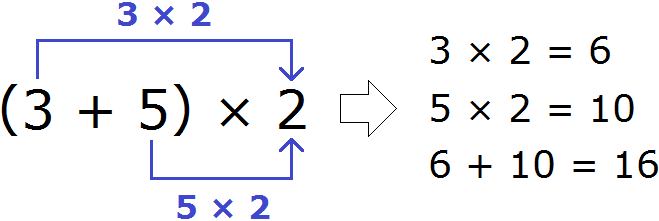
Рассмотрим следующее выражение:

Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:

В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:

8 × 2 = 16

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:

Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

(3 + 5) × 2 = 6 + 10 = 16

Теперь запишем распределительный закон умножения с помощью переменных:

(a + b) × c = a × c + b × c

Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.

Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×

Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.

c × (a + b) = c × a + c × b

Пример 2. Найти значение выражения 5 × (3 + 2)

Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Пример 3. Найти значение выражения 6 × (5 + 2)

Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:

6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42

Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.

Пример 4. Найти значение выражения 5 × (6 − 2)

Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20

Пример 5. Найти значение выражения 7 × (3 − 2)

Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

Источник