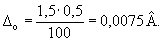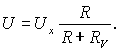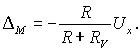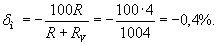Что такое расширенная неопределенность

Р 50.2.038-2004 ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений

РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ

Государственная система обеспечения
единства измерений

ИЗМЕРЕНИЯ ПРЯМЫЕ
ОДНОКРАТНЫЕ

Оценивание погрешностей и неопределенности
результата измерений

1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева Госстандарта России (ФГУП ВНИИМ им. Д.И. Менделеева)

ВНЕСЕНЫ Управлением метрологии Госстандарта России

2 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 октября 2004 г. № 43-ст

3 ВЗАМЕН МИ 1552-86

РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ

Государственная система обеспечения единства измерений

ИЗМЕРЕНИЯ ПРЯМЫЕ ОДНОКРАТНЫЕ

Оценивание погрешностей и неопределенности результата измерений

State system for ensuring the uniformity of measurements.
Direct single measurements. Estimation of errors and uncertainty of measurements result

Дата введения 2005-01-01

1 Область применения

Настоящие рекомендации распространяются на нормативные, конструкторские, технические и другие документы, устанавливающие методики выполнения измерений (МВИ), и содержат методы оценивания характеристик погрешности и неопределенности результатов прямых однократных измерений. Разрабатываемые МВИ должны соответствовать требованиям ГОСТ Р 8.563.

Пример оценивания погрешности однократного измерения приведен в приложении А.

2 Нормативные ссылки

В настоящих рекомендациях использованы ссылки на следующие нормативные документы:

ГОСТ 8.207-76 Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения

ГОСТ 8711-93 ( МЭК 51-2-84) Приборы аналоговые показывающие электроизмерительные прямого действия и вспомогательные части к ним. Часть 2. Особые требования к амперметрам и вольтметрам

ГОСТ Р 8.563-96 Государственная система обеспечения единства измерений. Методики выполнения измерений

РМГ 43-2001 Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений»

РД 50-453-84 Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчета

МИ 1317-86 Государственная система обеспечения единства измерений. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров

3 Термины, определения, обозначения и сокращения

3.1 В настоящих рекомендациях применяют следующие термины с соответствующими определениями:

границы неисключенной систематической погрешности измерений: Границы интервала, внутри которого находится неисключенная систематическая погрешность измерений.

однократное измерение: Измерение, выполненное один раз.

неопределенность (измерений): Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине (по РМГ 43).

стандартная неопределенность и (измерений): Неопределенность результата измерений, выраженная в виде среднего квадратического отклонения (по РМГ 43).

1 Стандартную неопределенность, оцениваемую по типу А, u_A вычисляют по формуле

(1)

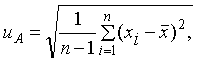
2 Стандартную неопределенность, оцениваемую по типу В, u_B вычисляют по формуле

(2)

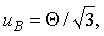
суммарная стандартная неопределенность u_c (измерений): Стандартная неопределенность ре зультата измерений, равная положительному квадратному корню суммы дисперсий (по РМГ 43).

расширенная неопределенность U (измерений): Границы интервала, в пределах которого нахо дится большая часть распределения значений, которые могли бы быть приписаны измеряемой величине.

3.2 В настоящих рекомендациях использованы следующие сокращения:

3.3 В настоящих рекомендациях использованы следующие обозначения:

— среднее арифметическое значение экспериментальных данных;

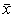
U — расширенная неопределенность;

U (Р) — расширенная неопределенность для уровня доверия Р;

S (Ã) — СКО случайной погрешности результата измерений;

z_{P /2} — квантиль нормального распределения для доверительной вероятности Р ;

Θ(Р) — доверительные границы систематической погрешности измерения для доверительной вероятности Р ;

т — число суммируемых НСП;

4 Общие положения

4.1 За результат однократного измерения Ã принимают значение величины, полученное при измерении.

4.2 На этапе перехода от погрешности к неопределенности целесообразно указывать характеристики и погрешности, и неопределенности результата измерения.

Составляющие погрешности результата измерения должны быть известны до проведения измерения. Предполагают, что известные систематические погрешности исключены (внесены поправки на все известные источники неопределенности, имеющие систематический характер).

4.3 Полагают, что распределение случайных погрешностей не противоречит нормальному распределению, а неисключенные систематические погрешности, представленные заданными границами ±Θ, распределены равномерно.

В целях количественного выражения неопределенности результата измерения, представленной в виде границ отклонения значения величины от ее оценки [- Θ; + Θ] (неполное знание о значении величины), полагают, что распределение возможных значений измеряемой величины в указанных границах не противоречит равномерному распределению.

4.4 Выполнение однократных измерений обосновывают следующими факторами:

— производственной необходимостью (разрушение образца, невозможность повторения измерения, экономическая целесообразность и т.д.);

— возможностью пренебрежения случайными погрешностями;

— случайные погрешности существенны, но доверительная граница погрешности результата измерения не превышает допускаемой погрешности измерений;

— стандартная неопределенность, оцениваемая по типу А, существенна, но расширенная неопределенность не превышает заданного предела.

1 Случайные погрешности считают пренебрежимо малыми по сравнению с неисключенными систематическими, если

S( Ã) — СКО случайных погрешностей результата измерения.

2 Неопределенность, оцениваемую по типу А, считают пренебрежимо малой по сравнению с неопределенностью, оцениваемой по типу В, если выполняется условие

(4)

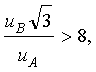
4.5 При определении доверительных границ погрешности или расширенной неопределенности для уровня доверия Р результата измерения принимают вероятность, равную 0,95.

В особых случаях, например при измерениях, которые нельзя повторить, допускается указывать доверительные границы или расширенную неопределенность для уровня доверия Р и более высоких вероятностей.

4.6 При вычислениях следует пользоваться правилами округления в соответствии с МИ 1317. Доверительные границы погрешности (характеристики погрешности) и расширенная неопределенность (расширенная неопределенность для уровня доверия Р) результата измерения должны быть представлены не более чем двумя значащими цифрами.

5 Составляющие погрешности и неопределенности результата измерения

5.1 Составляющими погрешности результата однократного измерения являются погрешности СИ, метода, оператора, а также погрешности, обусловленные изменением условий измерения.

5.2 Погрешность результата однократного измерения чаще всего представлена НСП и случайными погрешностями.

Неопределенность результата однократного измерения может быть представлена стандартными неопределенностями, оцениваемыми по типам А и В.

5.3 Характеристикой НСП могут быть:

5.4 Характеристикой случайных погрешностей могут быть:

— доверительные границы ± e (Р).

5.5 Погрешность СИ определяют на основании их метрологических характеристик, которые должны быть указаны в нормативных и технических документах, и в соответствии с РД 50-453.

5.6 Погрешности метода и оператора должны быть определены при разработке и аттестации конкретной МВИ.

6 Оценивание неисключенной систематической погрешности и стандартной неопределенности, оцениваемой по типу В, результата измерения

6.1 НСП результата измерения выражают границами этой погрешности, если среди составляющих погрешности результата измерения в наличии одна НСП.

6.2 Доверительные границы НСП результата измерения вычисляют следующим образом.

(5)

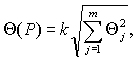
При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.

При доверительной вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если число суммируемых составляющих т > 4. Если же число составляющих равно четырем (т = 4), то поправочный коэффициент k ≈ 1,4; при т = 3 k ≈ 1,3; при т = 2 k ≈ 1,2. Более точное значение k для доверительной вероятности Р = 0,99 при числе составляющих т £ 4 в зависимости от соотношения составляющих l определяют по графику [ k = f ( m , l )] в соответствии с требованиями ГОСТ 8.207.

При условии, указанном в 6.2.1, суммарную стандартную неопределенность, оцениваемую по типу В, и_{с, B} вычисляют по формуле

(6)

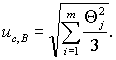
6.2.2 При наличии нескольких НСП, заданных доверительными границами Θ _j (Р _i ), рассчитанными по формуле ( 5), доверительную границу НСП результата однократного измерения вычисляют по формуле

(7)

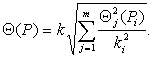
При условии, указанном выше, суммарную стандартную неопределенность, оцениваемую по типу В, вычисляют по формуле

(8)

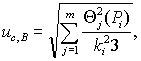
Значения коэффициентов k и k_i определяют в соответствии с требованиями 6.2.1.

7 Оценивание случайной погрешности и стандартной неопределенности, оцениваемой по типу А, результата измерения

7.1 Доверительные границы случайной погрешности и стандартную неопределенность, оцениваемую по типу А, результата измерения вычисляют следующим образом.

7.1.1 Если случайные погрешности представлены несколькими СКО S_i , то СКО результата однократного измерения S( Ã) вычисляют по формуле

(9)

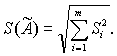
Учитывая условия 7.1.1, стандартную неопределенность, оцениваемую по типу А, результата однократного измерения и _A вычисляют по формуле

(10)

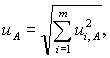
Доверительную границу случайной погрешности результата измерения e (Р) вычисляют по формуле

(12)

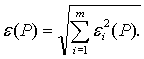
7.1.3 Если случайные погрешности представлены доверительными границами, соответствующими разным вероятностям, сначала определяют СКО результата измерения по формуле

(13)

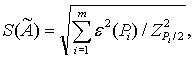
а затем вычисляют доверительные границы случайной погрешности результата измерения по формуле ( 11).

8 Оценивание погрешности и расширенной неопределенности результата измерения

8.1 Если погрешности метода и оператора пренебрежимо малы по сравнению с погрешностью используемых СИ (не превышают 15 % погрешности СИ), то за погрешность результата измерения принимают погрешность используемых СИ.

Расширенную неопределенность для уровня доверия Р вычисляют по формуле

(15)

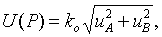
9 Форма представления результата измерения

9.1 Форма представления результатов однократных измерений должна соответствовать МИ 1317.

9.2 При симметричной доверительной погрешности результат однократного измерения представляют в форме Ã; ± D (Р); Р или Ã; ± D (Р), или Ã; U (Р).

Значение результата измерения должно оканчиваться цифрами того же разряда, что и значение погрешности или расширенной неопределенности для уровня доверия.

ПРИЛОЖЕНИЕ А
(справочное)

Расчет погрешности измерения напряжения показывающим прибором

Однократное измерение напряжения на участке электрической цепи сопротивлением R = 4 Ом.

А.1 Априорные данные об исследуемом объекте

Для измерения выбирают вольтметр класса точности 0,5 по ГОСТ 8711 (приведенная погрешность 0,5 %) с верхним пределом диапазона измерений U _{п p} = 1,5 В. Вольтметр имеет магнитный экран. Некоторый запас по точности средства измерений необходим из-за возможного наличия дополнительных погрешностей, погрешности метода и т.д.

Инструментальная составляющая погрешности определяется основной и дополнительной погрешностями.

Основная погрешность прибора указана в приведенной форме. Следовательно, предел допускаемой основной погрешности вольтметра

Дополнительная погрешность из-за влияния магнитного поля не превышает 1,5 % нормирующего значения прибора и равна ±0,0225 В (0,015 · 1,5). Дополнительная температурная погрешность, обусловленная отклонением температуры от нормальной (20 °С) на 10 °С, не превышает 60 % предела допускаемой основной погрешности, эта дополнительная погрешность равна ±0,0045 В (0,0075 · 0,6).

А.2 Оценивание погрешности результата измерения

Погрешность метода определяется соотношением между сопротивлением участка цепи R и сопротивлением вольтметра R_V . Сопротивление вольтметра известно: R_V = 1000 Ом. При подсоединении вольтметра к цепи исходное напряжение U_x изменяется на

Отсюда методическая погрешность D _M в абсолютной форме

Методическая погрешность δ_м в относительной форме

Оцененная методическая погрешность является систематической составляющей погрешности измерений и должна быть внесена в результат измерения в виде поправки 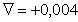В. Тогда результат измерения Ã с учетом поправки на систематическую погрешность

à = 0,90 + 0,004 = 0,904 В.

Находят границы погрешности результата измерения.

Поскольку основная погрешность применяемого средства измерений и его дополнительные погрешности заданы границами, следует рассматривать эти погрешности как неисключенные систематические. Воспользовавшись формулой ( 5), находят доверительную границу неисключенной систематической погрешности результата измерения при доверительной вероятности Р = 0,95:

Результат измерения в соответствии с разделом 9 следует представить в форме

à = 0,904 В; D (Р) = ±0,027 В; Р = 0,95 или (0,904 ± 0,027) В; Р = 0,95.

Ключевые слова: результат измерения, однократные измерения, среднее квадратическое отклонение, стандартная неопределенность, оцениваемая по типу А и по типу В, доверительная погрешность, расширенная неопределенность, коэффициент охвата, неисключенная систематическая погрешность

Источник

Мокров Ю. Метрология, стандартизация, сертификация

ОГЛАВЛЕНИЕ

Глава 5. Концепция неопределенности измерений

В 2003 г. введены в действие Рекомендации по межгосу-дарственной стандартизации РМГ 43-2001 «Применение «Руководства по выражению неопределенности измерений». Они распро-страняются на методы оценивания точности результатов измерений, содержат практические рекомендации по применению Руководства и показывают соответствие между формами представления результатов измерений с использованием погрешности и неопределен-ности измерений.
Руководство рекомендует выражать характеристики точности измерений в показателях неопределенности измерений, а не в показателях погрешности измерений, принятой в отечественной метрологической практике. Вместо понятия истинное значение измеряемой величины вводится понятие оцененное значение.
Вместо деления погрешностей по природе их появления на систематические и случайные вводится деление по способу оценивания неопределенностей – методами математической статистики или иными методами.
Причин появления концепции неопределенности измерений довольно много, но основные из них следующие.

5.1 Основные положения концепции неопределенности измерений

В Руководстве вместо понятия «погрешность измерения» вводится понятие «неопределенность измерения». При этом неопределенность измерения трактуется в двух смыслах:

Стандартная неопределенность по типу В используется для оценки величины x, которая не была получена в результате повторных наблюдений. Связанная с ней оцененная стандартная неопределенность uВ(xi) определяется на базе научного суждения, основанного на всей доступной информации о возможной изменчивости х. Фонд такой информации может включать:

Можно рекомендовать следующую процедуру оценивания и выражения неопределенности.

уровень доверия р, % коэффициент охвата k
68,27 1
90 1,645
95 1,960
95,45 2
99 2,576
99,73 3

5.2 Сопоставление концепций погрешности и неопределенности измерений

5.3 Использование концепции неопределенности

В связи с появлением Руководства и ряда отечественных документов по использованию неопределенности измерений, возникает вопрос, следует ли полностью отказаться от концепции погрешности измерений и перейти на принципы, изложенные в Руководстве. Среди метрологов нет единого мнения в этом вопросе. Так, в упомянутом выше РМГ 43-2001 говориться, что концепцией неопределенности целесообразно пользоваться при проведении совместных работ с зарубежными странами, при подготовке публикаций в зарубежной печати в при выполнения международных метрологических работ.
Кроме того, ряд авторов предлагает для тех видов и групп средств измерений, которые обеспечены поверочными схемами, восходящими к государственным эталонам, сохранить концепцию погрешности измерений. Это объясняется тем, что величины, воспроизводимые эталонами, имеют наивысшую на данный момент времени точность и воспринимаются как истинные значения величин.
Для тех же видов и средств измерений, которые не обеспечены государственными эталонами и поверочными схемами, можно использовать концепцию неопределенности измерений и разрабатывать документацию в соответствии с Руководством.

Источник

Расширенная неопределенность

Общие положения

Определение расширенной неопределенности

Коррелированные входные величины

5.2.1.Уравнение (10) и те уравнения, которые выведены из него, такие как (11)

и (12), справедливы только в том случае, если входные величины Xi независимы

или некоррелированы (считается, что инвариантами являются случайные

переменные, а не физические величины – см. 4.1.1., Примечание 1). 1). Если

какие-либо из Xi в значительной степени коррелированны, то корреляцию

необходимо брать в расчет.

5.2.2.Когда входные величины коррелированны, соответствующее выражение

для суммарной дисперсии uc2 (y),связанной с результатом измерения, будет

где хi и хj являются оценками Х_i и Х_j , а u(x_i, х_j)= =u( х_j, х_i) являются оцененной ковариацией, связанной с х_i и х_j. Степень корреляции между х_i и х_j характеризуется оцененным коэффициентом корреляции

В терминах коэффициентов корреляции, которые легче истолковать, чем

5.2.5.Корреляция между входными величинами нельзя игнорировать, если они

имеются и значительны. Связанные с ними ковариации следует оценивать экспериментально, если это возможно, изменяя коррелированные входные

величины (см.С.3.6. Примечание 3) или используя всю имеющуюся

информацию о коррелированной изменчивости рассматриваемых величин

(оценивание ковариации по типу В). Правильное понимание, базирующееся на

прошлом опыте и общих знаниях (см.4.3.1 и 4.3.2), особо необходимо при

оценивании степени корреляции между входными величинами, возникающей

из-за эффектов, оказывающих общие влияния, таких как температура

окружающей среды, атмосферное давление и влажность. К счастью, во многих

случаях эффекты таких влияний имеют пренебрежимо малую взаимосвязь, так

что можно предположить, что входные величины, испытывающие такие

влияния, некоррелированы. Однако, если нельзя предположить, что они

некоррелированы, сами корреляции могут быть исключены, если общие

влияния введены как добавочные независимые входные величины, как указано

6.2.1.Дополнительная мера неопределенности, которая соответствует

требованию указания интервала, как упомянуто в 6.1.2, называется

расширенной неопределенностью и обозначается символом U. Расширенную

неопределенность U получают путем умножения суммарной стандартной

неопределенности u_c(y) на коэффициент охвата k

Тогда результат измерения удобно выражается как Y = y ± U, что означает, что

6.2.2.Термины «доверительный интервал» и «уровень доверия» имеют в

статистике специальные определения и применяются к интервалу,

определяемому U, только когда выполнены определенные условия, включая

условие, чтобы все составляющие неопределенности, которые входят в u_c(y),

были бы получены из оценивания по типу А. Таким образом, в данном

Руководстве слово «доверие» не используется для модификации слова

«интервал», когда ссылаются на интервал, определяемый U; и термин

«доверительный уровень» также не используется в связи с интервалом и

предпочитается скорее термин «уровень доверия». Более конкретно, U

рассматривается как задание интервала вокруг результата измерения, который

содержит большую часть р распределения вероятностей, характеризуемого

стандартной неопределенностью, и р является «вероятностью охвата» или

«уровнем доверия» для этого интервала.

6.2.3.Если это возможно, необходимо оценить и указать доверительный

уровень р, связанный с интервалом, определяемым U. Надо признать, что

умножение u_c(y) на какую-то постоянную величину не дает никакой новой

информации, а просто представляет ранее имевшуюся информацию в новом

виде. Однако нужно также признать, что в большинстве случаев уровень

доверия р (особенно для значений р, близких к 1) будет скорее неопределенным не только из-за ограниченного знания распределения вероятностей, характеризуемых y и u_c(y) (особенно в крайних областях), но также из-за неопределенности самой u_c(y).

Источник