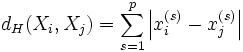Что такое расстояние хэмминга и что оно показывает

Расстояние Хемминга

Расстояние Хэмминга — мера (точнее, метрика) различия объектов одинаковой размерности.

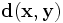
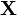
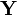
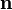
Первоначально метрика была сформулирована Ричардом Хэммингом во время его работы в Bell Labs для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей, в этом случае расстоянием Хэмминга между двумя двоичными последовательностями (векторами) и длины называется число позиций, в которых они различны — в такой формулировке расстояние Хэмминга вошло в Словарь алгоритмов и структур данных Национального Института Стандартов США (англ. NIST Dictionary of Algorithms and Data Structures ).

Так, расстояние Хэмминга между векторами 0 01 1 1 и 1 01 0 1 равно 2 (красным отмечены различающиеся биты). В дальнейшем метрика была обобщена на q-ичные последовательности: для пары строк « вы бор ы » и « за бор а » расстояние Хэмминга равно трём.

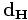
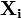
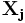
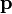
В общем виде расстояние Хэмминга для объектов и размерности задаётся функцией:

Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:

Содержание

Расстояние Хэмминга в биоинформатике и геномике

При эволюционном расхождении гомологичных ДНК-последовательностей расстояние Хэмминга является мерой, по которой можно судить о времени, прошедшем с момента расхождения гомологов, например, о длительности эволюционного отрезка, разделяющего гены-гомологи и ген-предшественник.

Родственные методы

Литература

Ссылки

Полезное

Смотреть что такое «Расстояние Хемминга» в других словарях:

расстояние Хемминга — хемминговское расстояние Расстояние d (u,v) между двумя кодовыми последовательноаями u и v одинаковой длины, равное числу символов, в которых они отличаются. Блочный код с минимальным хемминговским расстоянием d позволяет обнаружить (d 1) и… … Справочник технического переводчика

кодовое расстояние — Минимум расстояния Хемминга, взятый по всем ларам различных кодовых слов в равномерном коде. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] Тематики теория… … Справочник технического переводчика

Линейный код — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия

Порождающая матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия

Проверочная матрица — В области математики и теории информации линейный код это важный тип блокового кода, использующийся в схемах определения и коррекции ошибок. Линейные коды, по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы… … Википедия

Обнаружение и исправление ошибок — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления… … Википедия

Избыточное кодирование — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия

Избыточность данных — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия

Исправляющие ошибки Коды — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия

Коды, исправляющие ошибки — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия

Источник

Код Хэмминга. Пример работы алгоритма

Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.

Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.

Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.

Как это работает.

Для того, чтобы понять работу данного алгоритма, рассмотрим пример.

Подготовка

Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.

На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

и

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):

Было:

Стало:

Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».

Вычисление контрольных бит.

Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:

Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.

Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.

Декодирование и исправление ошибок.

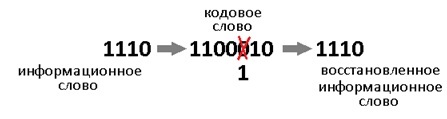
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.

Заключение.

В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.

Примечание.

На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.

Источник

Помехоустойчивое кодирование. Часть 1: код Хэмминга

Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.

Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.

Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.

Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.

К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:

Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).

Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):

Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.

Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:

Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.

В результате собираем список синдромов, и то на какую болезнь он указывает:

Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.

Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.

А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):

Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:

Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:

Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:

Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.

Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.

Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:

Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.

Список используемой литературы:

1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986

Источник

Распознаем текст, используя расстояние Хэмминга

Итак, мы собираемся написать программу на Delphi (я использую версию 6), способную перевести символы с картинки в текст. Задача довольно популярная в интернете, и на каждый пост «Хочу реализовать распознавание символов. Помогите» самые частые ответы «почитай в интернете» либо «не берись, используй файнридер» и тому подобное.

Я, как и многие другие, начал с изучения основных алгоритмов. Конечно, такие монстры как FineReader тратят на алгоритмическую составляющую огромные деньги, и их секретов нам не узнать, но прочей информации было найдено приличное количество, чтобы понять основные методы. Но начнем издалека.

Суть распознавания – сравнение с образом.

В детстве, смотря на текст, мы видим всего лишь картинку. Мы ещё не наделены необходимыми критериями её анализа, для того чтобы понять, что на картинке не просто рисунок, а текст, и не просто текст, а какой-то рассказ. Мы растём, и начинаем получать образы символов, узнаём что рисунок с буквой «А» обозначает букву А, а не пароходик. Становясь старше, мы набираем базу образов (или базу критериев образов), по которой путем сравнения и анализа мы можем сказать, какой символ перед нами.
Точно такая же ситуация и с компьютером. Сперва он просто получает в память картинку, затем ищет на ней какие-то области, и после этого сравнивает эти области со своей базой и проводит анализ, результатом которого будет определение символа на изображении. На словах всё просто – передаем в память картинку, ищем на картинке какие-то области, сравниваем с базой, но методы сравнения картинки до сих пор непонятны. Идём в интернет.

Методы сравнения

Современные методы сравнения изображения делятся на две категории:

1.Сравнение с эталоном
2.Сравнение по критериям

И особняком стоит между ними метод нейронных сетей, поскольку применим в обоих случаях. Использовать его и рассматривать его работы мы не будем, постараемся сделать всё максимально просто и понятно.

Сравнение по критериям наиболее трудоёмко, потому что выполнить алгоритмическую задачу по определению характерных черт символа сложно, да и эффективность подобного алгоритма будет наверняка небольшой. Связано это со схожестью символов, а если мы будем распознавать текст низкого разрешения, то затрат на оттачивание подобного алгоритма будет в разы больше. Однако для столь сложной задачи был найден исходник с решением.

Также были найдены исходники незамысловатых программ, проверяющих крайние точки и точки изгибов на наличие черной области:
Распознавание почтовых индексов
Распознавание картинок Яндекса(CY)

Проблемы распознавания данных программ налицо – при несоответствии изображений(а также наличии шума, посторонних объектов и т.д.) данные программы малоэффективны. Однако они на ура справляются с узким кругом поставленных для них задач. Мы же хотим получить более универсальный пример реализации распознавания.

Сравнение с эталоном – задача более простая и более эффективная. Тут всё максимально просто — создать эталонное изображение и сравнить их. Методов сравнения довольно много – попиксельное, наложение, наложение со смещением и прочие. Статьями по этой теме интернет наполнен сполна. Наиболее интересные работы:
Распознавание образов мобильным роботом
Применение нейросетей в распознавании изображений
Реализация простейшего алгоритма распознавания графических образов

Мы будем использовать самый простой метод сравнения – попиксельный. Суть – поочередное сравнение двух соответствующих пикселей двух черно-белых картинок. Поскольку два пикселя должны быть соответствующими, то картинки должны быть одинаковы по размеру.

Сравнение очень долгий алгоритм, поэтому мы должны оптимизировать работу нашей программы на сравнение не двух картинок скажем 100х100 пикселей(10 000 операций сравнения), а что-то меньшее, но всё также актуальное (сравнивая картинки 8х8 пикселей, различить в них букву довольно сложно даже человеку, поэтому, чем больше пикселей мы берём, тем больше вероятность правильности распознавания и тем большее время требует наш алгоритм). Экспериментальным путём был выбран оптимальный размер – 16х16 пикселей. Но перед изменением размера необходим ещё найти то, что будем изменять.

Выделение

см. function TForm1.PreParse1(Pic:TPicture):string;
Итак, нам необходимо найти на картинке символы, причем найти их все. Для этого картинка переводится в черно-белую (см. procedure TForm1.Mono(Bmp:TBitmap)), и ищутся все объекты через сравнение с крайними пикселями предположительного символа. Вокруг каждого найденного символа строится рамка красного цвета, именно по этой рамке происходит изменение размера изображения (функция StretchBlt) и его копирование для сравнения (см. function TForm1.Parce3(Pic:TPicture;x1, y1, x2, y2: Integer): TBitmap;)

Алгоритм сравнения

См. function TForm1.ParceBMP(bmp1:Tbitmap):string;
Алгоритм прост – сравниваем попиксельно (см. function TForm1.Compare(b1,b2:TBitmap):integer), если два пикселя разные (один черный, другой белый), то увеличиваем счетчик R. После полного сравнения двух картинок подставляем счетчик в формулу

Значение, полученное в результате сравнения, получило название «расстояние Хэмминга».
Затем формируем массив результатов вычислений по данной формуле для разных сравнений (наша картинка со всеми эталонами). Берём максимальное значение массива и соответствующий ему символ. Это наш результат!

Составление базы

Следующий этап работы нашей программы – составление базы (массив записей символа и его графического представления). Мы сделаем стандартную базу изображений русских символов и цифр без применения графических редакторов – в исходном коде. Для этого потребуется задать изображение нужного размера, открыть режим канвы, и написать в изображении необходимую букву.
Тут же необходимо обработать полученную картинку так, как мы обрабатываем исходную, чтобы эталон был максимально приближен к распознаваемой картинке и наоборот (об этом читай ниже).

Var
myarray:array of record //задаем наш массив
ch:char; //символ
bmp:TBitmap; //соответствующее ему изображение
end;
i : integer; //счетчик
Img:TBitmap; //промежуточное(буферное) изображение
im:TPicture; //то же изображение, для передачи на обработку
begin
SetLength(myarray, 73);//выделяем массиву память
im:=TPicture.Create; //создаем необходимые объекты
Img:=TBitmap.Create;
for i := 0 to 31 do
with Img.Canvas do //открываем канву
begin
Img.Height:=16; //задаем ширину и высоту
Img.Width:=16;
Brush.Color := clWhite; //чертим белый фон
Pen.Color := clWhite;
Rectangle(0,0,16,16); //используя инструмент квадрат
Pen.Color := clBlack; //ставим ручке черную краску
Font.Color := clBlack;
Font.Charset:=form1.FontDialog1.Font.Charset; //выбираем шрифт (пользователь выбирает шрифт для базы) и его параметры
Font.Size := Form1.FontDialog1.Font.Size;
Font.Style := Form1.FontDialog1.Font.Style;
Font.Name := Form1.FontDialog1.Font.Name;
TextOut(0, 0, CHR(ORD(‘А’)+i));//пишем в нашем изображении
myarray[i].bmp:=TBitmap.Create;//создаем объект в массиве
myarray[i].ch:=CHR(ORD(‘А’)+i);//задаем что это за символ соответственно
im.Bitmap.Assign(Img);//задаем картинке изображение
myarray[i].bmp:=PreParse2(Im);//посылаем на обработку и присваиваем выходную картинку элементу массива(описание будет немного позже
end;

Ошибки

Куда же без них? Нам понадобится также метод обработки ошибок распознавания. Для этого перед распознаванием мы должны сделать специальную кнопочку, которая будет показывать символы и результат работы программы, и спрашивать нас, верно ли распознавание. Если да, то ничего не делать, иначе заносить в базу, структура которой следующая – файл-индексатор, в котором задается количество символов в базе, следующие строки – символ, и ссылка на файл с изображением (см. procedure TForm1.Learn(Pic:TPicture);).

Краткая блок-схема

Реализация

Определяем задачи и рисуем форму:

Скрин работающей программы:

Что упущено или планы на будущее

— Не может программа распознавать буквы, состоящие из двух фигур: Ы, Й.
— При повороте/шумах/прочее распознавание не корректно.
— Порой распознает маленькие буквы как большие, большие как маленькие (что собственно логично для данного метода)

Вывод

Вот и написан очередной «распознаватель» текста. Кому он пригодится? Практически никому. Это не FineReader, и не Cuneiform. Тут всё намного проще и понятнее, и менее эффективно. Но, несмотря на это надеюсь, эта статья будет полезна ИТ-сообществу. Данная система может быть изменена под какие-либо другие нужды.

В недалёком будущем хочу дополнить рассказ графиками результатов распознавания, а также сравнением данного метода распознавания с другими.

UPD: были проблемы с базой, решил, исходник перезалил, спасибо AmoN’у

Источник