Что такое расстояние между концами отрезка

Урок 3 Бесплатно Отрезок. Длина отрезка

Начнем знакомство с одним из разделов математики, который называется геометрия.

Становление данной науки происходило тысячелетиями.

Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.

Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.

Научимся сравнивать, находить длины отрезков.

Познакомимся с различными единицами измерения отрезков.

Рассмотрим свойства измерения длин отрезков.

Отрезок

Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).

Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.

Одной такой элементарной фигурой является точка.

В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.

Слово «точка» с латинского языка означает мгновенное касание, укол.

Точку принято рассматривать как некоторое место в пространстве или на плоскости.

Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).

Две точки на плоскости можно соединить бесконечным множеством линий.

Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.

Кратчайшая линия между двумя точками называется отрезком.

Любые две точки можно соединить только одним отрезком.

Точки, ограничивающие отрезок, называются концами отрезка.

Отрезок обозначают указанием имен его концов.

Через точки А и В с помощью линейки провели прямую.

Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.

Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».

В названии отрезка не важно в каком порядке указываются его концы.

Отрезок можно построить с помощью линейки.

Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.

Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:

Между точками А и В отметить точку С.

Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.

Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.

У меня есть дополнительная информация к этой части урока!

Давайте разберемся, как могут располагаться точки по отношению к отрезку:

1. Точка лежит на отрезке.

Говорят: «Точка G принадлежит отрезку ».

Записывают это так: G ∈ AB

2. Точка не лежит на отрезке.

Говорят: «Точка не принадлежит отрезку ».

Записывают это так: R ∉ AB

Пройти тест и получить оценку можно после входа или регистрации

Длина отрезка

Каждый отрезок имеет определенную длину, значение которой является числом.

Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.

Существует несколько способов сравнения отрезков.

1. Приблизительный способ сравнения.

Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.

Пример: Даны два отрезка АВ и ЕР

Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР

Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.

По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.

Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).

Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).

Пример: Даны два отрезка АВ и ОЕ

Сравним данные отрезки методом совмещения отрезков.

Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.

Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.

Значит, отрезок ОЕ короче отрезка АВ.

Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.

3. Сравнение отрезков с помощью измерителя.

Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.

В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.

Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.

Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.

Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.

В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.

Пусть даны три отрезка СD, АЕ, BG

Сравним эти отрезки с помощью циркуля.

Соединим ножки циркуля с концами С и D отрезка СD.

Приложим циркуль с заданным раствором к отрезку АЕ.

Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).

Приложим циркуль с заданным раствором к отрезку BG.

Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).

Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.

4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.

Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.

Большим будет являться тот отрезок, длина которого больше.

Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.

У меня есть дополнительная информация к этой части урока!

Ломаная линия

Если последовательно соединить отрезки так, чтобы конец одного отрезка являлся началом следующего (при этом соседние отрезки не лежат на одной прямой), то образуется геометрическая фигура, которая называется ломаной линией.

Отрезки, из которых состоит ломаная линия, называют звеньями.

Концы отрезков называют вершинами ломаной.

Самые крайние вершины ломаной называют концами ломаной

Обозначение ломаной линии составляют из названий вершин этой ломаной, называя их по порядку.

Длиной ломаной называется сумма длин всех ее звеньев.

На рисунке изображена ломаная линия АBCDE.

Вершины ломаной АBCDE: А, B, C, D, Е.

Звенья ломаной АBCDE: AB, BC, CD, DE.

Найдем длину ломаной АВСDE:

АВСDE = AB+ BC+ CD+ DE = 2 см + 3 см + 4 см + 5 см = 14 см

Ломаная, концы которой совмещаются, называется замкнутой.

Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.

Отрезки (звенья) ломаной линии называют сторонами многоугольника.

Общие точки двух отрезков (сторон) многоугольника называют его вершинами.

Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.

Количество сторон и количество углов в многоугольнике совпадают.

Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.

Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.

На рисунке изображен многоугольник АBCDEF.

Вершины многоугольника АBCDEF: А, B, C, D, Е, F.

Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.

Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.

Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.

Периметр многоугольника принято обозначать заглавной латинской буквой Р

Найдем периметр многоугольника АBCDEF (изображенного на рисунке):

Р_АВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.

Существует огромное множество различных видов многоугольников.

Обычно многоугольники различают по числу сторон и углов.

Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.

Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.

На рисунке изображен треугольник АBC (Δ АBC).

Отрезки AB, BC, АC— стороны треугольника АBC.

Периметр треугольника- это сумма длин трех его сторон.

Найдем периметр треугольника АBC (изображенного на рисунке):

Р_АВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Отрезок. Формула длины отрезка.

Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.

Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).

В данном примере вектор AB задан координатами (х₂— х₁, y₂— y₁). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:

Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек

Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х₁y₁) и (х₂,у₂).

Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.

Установим длину этих проекций.

В рассмотренном случае |AB| выступает длиной отрезка.

Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.

Источник

Длина отрезка

Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.

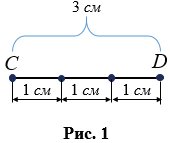
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

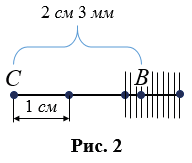
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

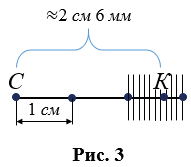
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:

За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.

Свойства длин отрезков:

Поделись с друзьями в социальных сетях:

Источник

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Середина отрезка – это точка, делящая его пополам, т.е. на два равных отрезка.

Две фигуры, имеющие одинаковую форму и одинаковые размеры, называют равными.

Две геометрические фигуры называются равными, если их можно совместить наложением.

Длина отрезка – это расстояние между концами этого отрезка.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Теоретический материал для самостоятельного изучения.

«Измерь самого себя – и ты станешь настоящим геометром!» – однажды сказал средневековый философ Марсилио Фичино.

И в этом есть доля правды, ведь измерения – это одно из важных действий в геометрии.

Поэтому сегодня мы будем измерять данный отрезок с помощью линейки и выражать результат в выбранной единице измерения.

В жизни часто приходится измерять длины, будь то длина дороги или ширина комнаты. В геометрии мы будем измерять отрезки. На чём же основано измерение отрезков?

Основа любого измерения – это сравнение величин с другими, принятыми за единицу измерения этой величины.

То же самое и с измерением длины отрезка. Т.е. измерение отрезка – это сравнение длины отрезка с некоторым другим отрезком (масштабным), выбранным за единицу измерения.

Если взять за единицу измерения сантиметр, то, определяя длину отрезка, мы узнаём, сколько раз в заданном отрезке укладывается сантиметр.

Например, один сантиметр укладывается в отрезке АВ семь раз, следовательно, длина отрезкасемь сантиметров.

Если масштабный отрезок не укладывается целое число раз в измеряемом отрезке, то единицу измерения делят ещё на части, обычно на десять. Далее, определяют, сколько такая часть укладывается в остатке.

Например, в отрезке АВ один сантиметр укладываетсятри раза, в остатке ровно 7 раз укладывается десятая часть сантиметра, а десятая часть сантиметра это миллиметр, т.е. длина отрезка АВ три сантиметра семь миллиметров или три целых семь десятых сантиметра.

Но бывает, что и при меньшем масштабном отрезке есть остаток, тогда говорят, что длина отрезка приближенно равна определенному значению.

Для более точного измерения этого отрезка указанную часть единицы измерения (в данном случае миллиметр) можно разделить на 10 равных частей и продолжить процесс измерения, но обычно так не делают, оставляют приближенное значение длины отрезка.

Стоит отметить, что за единицу измерения можно принимать не только сантиметр, но и любой другой отрезок. Например, метр, милю. А выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.

Два отрезка считаются равными, если единица измерения и её части укладываются в этих отрезках одинаковое число раз, т.е. равные отрезки имеют равные длины.

Если один отрезок меньше другого, то единица измерения (или её часть) укладываются в этом отрезке меньшее число раз, чем в другом, т.е. меньший отрезок имеет меньшую длину.

AD= 4 см + 1,2 см + 1,3 см = 6 см.

Таким образом, длина отрезка – это расстояние между концами этого отрезка.

Для измерения длины отрезкаиспользуют различные приборы: линейка, штангенциркуль, рулетка.

Итак, сегодня вы получили представлениео том, как измерять данный отрезок с помощью линейки и выражать результат в выбранной единице измерения.

Возьмём несколько отрезков и соединим их между собой друг за другом под углом, не равным 180 градусам, полученная фигура называется ломаной. Она может выглядеть так.

Если начало и конец ломанной совпадут, то она считается замкнутой ломаной.

При этом у ломаной можно определить длину, т.к. она состоит из отрезков, длину которых можно измерить. Поэтому длина ломанойравна сумме длин отрезков, из которых она состоит.

При этом,длина незамкнутой ломаной не меньше длины отрезка, соединяющего ее концы.

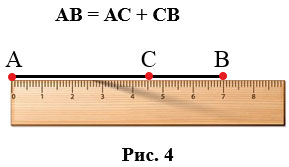
1. Какова длина отрезка АВ, если точка О делит отрезок АВ на две части, при этом АО = 5см, ОВ = 2,3 см?

По условию задачи, точка О делит отрезок АВ на две части, следовательно, длина отрезка АВ = АО + ОВ = 5см + 2,3 см =7,3 см.

2. На прямой а отмечены точки А, С, E, причём АС = 5 см, СE = 7 см. Чему может быть равна длина отрезка АE?

Для решения задачи нужно нарисовать рисунок в соответствии с условием. Тогда:

АЕ = АС + СЕ = 5см + 7см = 12 см.

А если точки поменять местами, АЕ = СЕ – СА = 7см – 5см = 2см. Других вариантов быть не может, поэтому получается два ответа.

Источник

Отрезок. Ломаная линия

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Рис. 2 Несколько отрезков на прямой

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

Рис. 4 Отрезок без прямой

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

Рис. 7 Построение произвольного отрезка

Измерить отрезок можно:

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

На рисунке 12 видно, что:

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

Источник