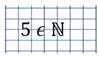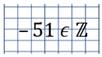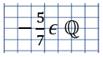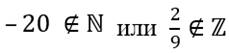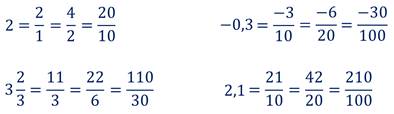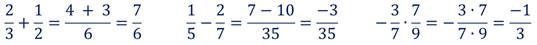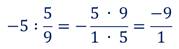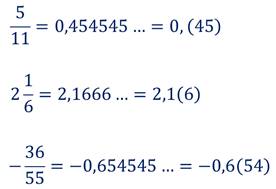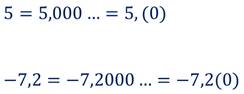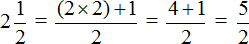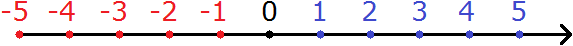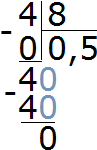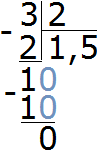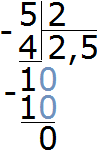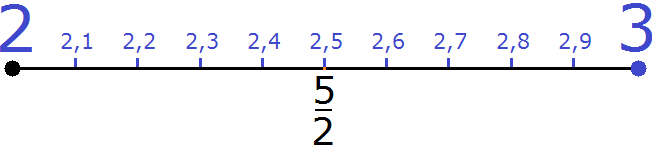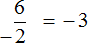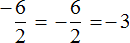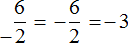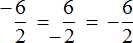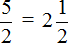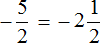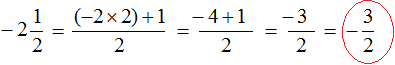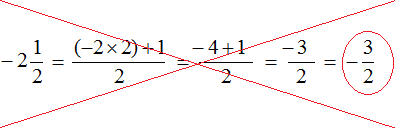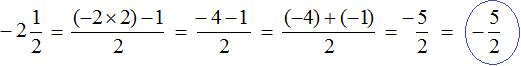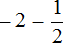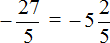Что такое рациональные числа в алгебре 8 класс

Алгебра. 8 класс

Все натуральные числа (1, 2, 3, 4, 5 и так далее) образуют множество натуральных чисел.
Множество натуральных чисел обозначается N.

При добавлении к натуральным числам противоположных им –1, –2, –3, –4, –5 и так далее, а также 0 образуется множество целых чисел.
Множество целых чисел обозначается Z.

Добавим к множеству целых чисел дробные числа – как положительные, так и отрицательные и так далее, получим множество рациональных чисел.
Множество рациональных чисел обозначается Q.

Рассмотрим число 3.
3 ∈ N: 3 принадлежит множеству натуральных чисел.
3 ∈ Z: 3 принадлежит множеству целых чисел.
3 ∈ Q: 3 принадлежит множеству рациональных чисел.

∈ – знак принадлежности к множеству.

Противоположное ему число: –3.
–3 ∉ N: –3 не принадлежит множеству натуральных чисел.

Каждое натуральное число входит и в множество целых чисел. Это значит, что множество натуральных чисел является подмножеством целых чисел. Множество N – подмножество Z.

Множество B является подмножеством C, если каждый элемент множества B, также принадлежит множеству C.

Множество Z является подмножеством Q, т. е. множество Z – подмножество Q. Z ⊂ Q.

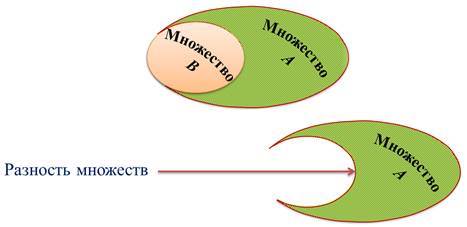
Множество дробных чисел, которое принадлежит Q, но не принадлежит Z, является разностью множеств Q и Z.

Разностью множеств B и C называется множество, состоящее из элементов, принадлежащих B, но не принадлежащих C.

Разность множеств B и C показана штриховкой.

Разностью множеств Z и N будет множество, состоящее из отрицательных целых чисел и нуля.

Разность множеств Z и N показана штриховкой.

Разностью множества, состоящего из чисел 1, 3, 5 и 7, и множества, состоящего из чисел 1 и 3, будет множество, элементы которого – числа 5 и 7.

Любое рациональное число (и целое, и дробное) можно представить в виде обыкновенной дроби , где m – целое число, а n – натуральное.

Рассмотрим примеры.

Представим число в виде десятичной дроби, разделив числитель 3 на знаменатель 8. Проведя деление в столбик, получим:

Представим теперь число в виде десятичной дроби, разделив числитель 1 на знаменатель 9 в столбик. В остатке всегда остаётся 1, и деление будет продолжаться бесконечно.

– бесконечная десятичная дробь.
– периодическая дробь. Период дроби равен 1.

Дробь обращается в бесконечную десятичную дробь. Такие бесконечные дроби называют периодическими, а повторяющиеся цифры – периодом дроби. Цифры периода пишут один раз и заключают в скобки.

Вообще, каждое дробное число можно представить в виде десятичной дроби: конечной или бесконечной.

Приведём несколько примеров.

Конечную десятичную дробь, и любое целое число можно представить в виде бесконечной десятичной дроби, если приписать справа бесконечное количество нулей.

Приведём несколько примеров.

Вывод: любое рациональное число можно представить в виде бесконечной десятичной периодической дроби.

Верно и обратное.
Каждая бесконечная десятичная периодическая дробь представляет какое-то рациональное число.

Приведём несколько примеров.

Разные бесконечные дроби представляют разные рациональные числа.

Исключение:
0,(9) = 1,(0) = 1,0000… = 1
3,2(9) = 3,3(0) = 3,30000… = 3,3 и так далее.

Дроби с периодом 9 принято заменять на дроби с периодом 0 и таким образом получая конечную десятичную дробь или целое число.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

Источник

Рациональные числа, понятие и примеры.

Рациональные числа вы с ними уже знакомы, осталось только обобщить и сформулировать правила. Так какие числа называются рациональными числами? Рассмотрим подробно в этой теме урока.

Понятие рациональных чисел.

Определение:
Рациональные числа – это числа, которые можно представить в виде дроби \(\frac\), где m – целое число, а n – натуральное число.

Другими словами, можно сказать:

Рациональные числа – это все натуральные числа, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Разберем каждый пункт подробно.

Множество рациональных чисел.

Вспомним, что множество натуральны чисел обозначается латинской буквой N.
Множество целых чисел обозначается латинской буквой Z.
А множество рациональных чисел обозначается латинской буквой Q.

Во множество рациональных чисел входит множество целых и натуральных чисел в этом и заключается смысл рациональных чисел.

На рисунке можно показать множество рациональных чисел.

Но не все числа являются рациональными. Бывают еще множества различных чисел, которые в дальнейшем вы будите изучать.
Бесконечные непрериодические дроби не принадлежат множеству рациональных чисел.
Например, число е, \(\sqrt<3>\) или число \(\pi\) (читается число пи) не являются рациональными числами.

Записать число 1 в виде рационального числа?
Ответ: чтобы записать в виде рационального число 1 нужно представить его в виде дроби 1=\(\frac<1><1>\).

Докажите, что число \(\sqrt<0,0049>\) является рациональным?
Доказательство: \(\sqrt<0,0049>=0,07\)

Является ли простое число под корнем рациональным числом?
Ответ: нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому не является рациональным числом.

Источник

Рациональные числа

Урок 9. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Рациональные числа»

Числа появились в практической деятельности для подсчета количества предметов. Такие числа, кроме нуля, называют натуральными числами. Они образуют множество натуральных чисел.

От первой буквы латинского слова naturalis – естественный, природный.

Если к натуральным числам присоединить число нуль и противоположные им числа (т.е. целые отрицательные числа), то получится множество целых чисел.

От первой буквы немецкого слова zahl – число.

А если к множеству целых чисел присоединить все дробные числа (положительные и отрицательные), то получится множество рациональных чисел.

От первой буквы французского слова quotient – отношение.

Для того чтобы записать, что какое-либо число принадлежит рассматриваемому множеству, используют вот такой знак принадлежности .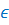

Введённые обозначения множеств чисел и знак принадлежности позволяют кратко записывать утверждения.

«Число 5 принадлежит множеству натуральных чисел»

«Число –51 принадлежит множеству целых чисел»

«Число −5/7 является рациональным числом»

Число не принадлежит множеству:

Теперь рассмотрим, понятие подмножества.

Пусть есть некоторые два множества А и В.

Пусть каждый элемент множества В является элементом множества А.

В таких случаях, говорят, что множество В является подмножеством множества А.

Для записи этого утверждения также есть определенный знак 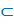, называют его знаком включения (т.е. одно множество содержится в другом).

Записывают это утверждение так:

а читают: В – подмножество множества А.

Понятие разности множеств.

Разностью множеств А и В называется множество, состоящее из всех элементов, которые принадлежат множеству А и не принадлежат множеству В.

Например, разность множества целых чисел и множества натуральных чисел является множество, состоящее из всех целых отрицательных чисел и нуля.

Вернёмся к рациональным числам. Вы уже знаете, что любое рациональное число, как целое, так и дробное, можно представить в виде дроби , где m – целое число, n – натуральное. Одно и то же рациональное число можно представить в таком виде разными способами.

Сумма, разность и произведение рациональных чисел, тоже рациональные числа. Например:

Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.

Обыкновенную дробь можно перевести в десятичную.

Бесконечные десятичные дроби такого вида называют периодическими. В периодических дробях повторяется одна или несколько цифр. Повторяющиеся цифры называют периодом. При записи периодических десятичных дробей период пишут один раз, заключая его в круглые скобки: читают эту запись так «нуль целых и 63 в периоде».

Замечание: любое рациональное число можно записать не только в виде обыкновенной дроби, но и в виде десятичной (конечной десятичной дроби), либо в виде бесконечной десятичной периодической дроби.

Любое целое число и любую конечную десятичную дробь можно записать в виде бесконечной десятичной периодической дроби. Для этого нужно приписать справа в качестве десятичных знаков бесконечную последовательность нулей.

Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби.

Верно и обратное утверждение: любая бесконечная десятичная периодическая дробь есть рациональное число.

Любое рациональное число, как целое, так и дробное, можно представить в виде дроби , где m – целое число, n – натуральное.

Сумма, разность и произведение рациональных чисел, тоже рациональные числа.

Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.

Любое рациональное число можно записать не только в виде обыкновенной дроби, но и в виде десятичной (конечной десятичной дроби), либо в виде бесконечной десятичной периодической дроби.

Любая бесконечная десятичная периодическая дробь есть рациональное число.

Источник

Рациональные числа

Тема рациональных чисел достаточно обширна. О ней можно говорить бесконечно и писать целые труды, каждый раз удивляясь новым фишкам.

Чтобы не допускать в будущем ошибок, в данном уроке мы немного углубимся в тему рациональных чисел, почерпнём из неё необходимые сведения и двинемся дальше.

Что такое рациональное число

К рациональным числам относятся следующие категории чисел:

Пример 1. Целое число 2 может быть представлено в виде дроби . Значит число 2 относится не только к целым числам, но и к рациональным.

Пример 2. Смешанное число может быть представлено в виде дроби . Данная дробь получается путём перевода смешанного числа в неправильную дробь

Значит смешанное число относится к рациональным числам.

Пример 3. Десятичная дробь 0,2 может быть представлена в виде дроби . Данная дробь получилась путём перевода десятичной дроби 0,2 в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему десятичных дробей.

Поскольку десятичная дробь 0,2 может быть представлена в виде дроби , значит она тоже относится к рациональным числам.

Пример 4. Бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби . Данная дробь получается путём перевода чистой периодической дроби в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему периодические дроби.

Поскольку бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби , значит она тоже относится к рациональным числам.

В дальнейшем, все числа которые можно представить в виде дроби, мы всё чаще будем называть одним словосочетанием — рациональные числа.

Рациональные числа на координатной прямой

Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:

На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.

Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.

Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.

Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей

Попробуем понять, почему дробь вдруг расположилась между нулём и единицей.

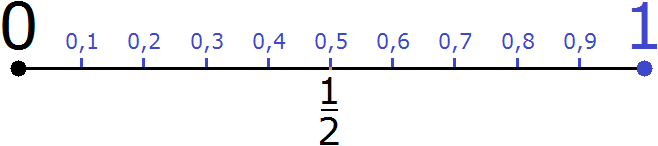
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину

Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.

Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5

Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.

Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь , а эта дробь также как и равна 0,5

А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь

Пример 2. Попробуем отметить на координатной рациональное число . Данное число располагается ровно между числами 1 и 2

Значение дроби равно 1,5

Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:

Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.

Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.

Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.

Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.

К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2

Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:

Пример 3. Отметим на координатной прямой рациональное число 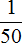. Данное рациональное число будет располагаться очень близко к нулю

Значение дроби 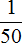равно 0,02

Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число

Видно, что наше рациональное число 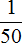расположилось там же, где и десятичная дробь 0,02.

Пример 4. Отметим на координатной прямой рациональное число 0, (3)

Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная

0,33333….и так далее до бесконечности..

И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.

Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3

Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.

Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3

это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.

Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь

Значение дроби равно 2,5

Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:

Видно, что наше рациональное число расположилось там же, где и десятичная дробь 2,5

Минус перед рациональным числом

В предыдущем уроке, который назвался умножение и деление целых чисел мы научились делить целые числа. В роли делимого и делителя могли стоять как положительные, так и отрицательные числа.

Рассмотрим простейшее выражение

В данном выражении делимое (−6) является отрицательным числом.

Теперь рассмотрим второе выражение

Здесь уже отрицательным числом является делитель (−2). Но в обоих случаях мы получаем один и тот же ответ −3.

Учитывая, что любое деление можно записать в виде дроби, мы можем рассмотренные выше примеры также записать в виде дроби:

А поскольку в обоих случаях значение дроби одинаково, минус стоящий либо в числителе либо в знаменателе можно сделать общим, поставив его перед дробью

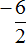
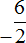
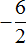
Поэтому между выражениями и и можно поставить знак равенства, потому что они несут одно и то же значение

В дальнейшем работая с дробями, если минус будет нам встречаться в числителе или в знаменателе, мы будем делать этот минус общим, ставя его перед дробью.

Противоположные рациональные числа

Как и целое число, рациональное число имеет своё противоположное число.

Например, для рационального числа противоположным числом является . Располагается оно на координатной прямой симметрично расположению относительно начала координат. Другими словами, оба этих числа равноудалены от начала координат

Перевод смешанных чисел в неправильные дроби

Мы знаем что для того, чтобы перевести смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части и прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель остаётся прежним..

Например, переведём смешанное число в неправильную дробь

Умножим целую часть на знаменатель дробной части и прибавим числитель дробной части:

Вычислим данное выражение:

Полученное число 5 будет числителем новой дроби, а знаменатель останется прежним:

Полностью данная процедура записывается следующим образом:

Чтобы вернуть изначальное смешанное число, достаточно выделить целую часть в дроби

Но этот способ перевода смешанного числа в неправильную дробь применим только в том случае, если смешанное число является положительным. Для отрицательного числа данный способ не сработает.

Рассмотрим дробь 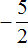. Выделим в этой дроби целую часть. Получим

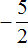
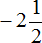
Чтобы вернуть изначальную дробь нужно перевести смешанное число в неправильную дробь. Но если мы воспользуемся старым правилом, а именно умножим целую часть на знаменатель дробной части и к полученному числу прибавим числитель дробной части, то получим следующее противоречие:

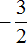
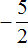
Мы получили дробь , а должны были получить дробь .

Делаем вывод, что смешанное число 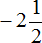в неправильную дробь переведено неправильно:

Чтобы правильно перевести отрицательное смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части, и из полученного числа вычесть числитель дробной части. В этом случае у нас всё встанет на свои места

Отрицательное смешанное число 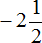является противоположным для смешанного числа . Если положительное смешанное число располагается в правой части и выглядит так

то отрицательное смешанное число 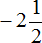будет располагаться в левой части симметрично относительное начала координат

И если читается как «две целых и одна вторая», то читается как «минус две целых и минус одна вторая». Поскольку числа −2 и располагаются в левой части координатной прямой — они оба являются отрицательными.

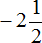
Любое смешанное число можно записать в развёрнутом виде. Положительное смешанное число в развёрнутом виде записывается как .

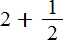
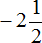
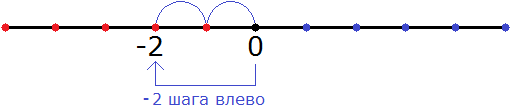
А отрицательное смешанное число записывается как

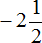
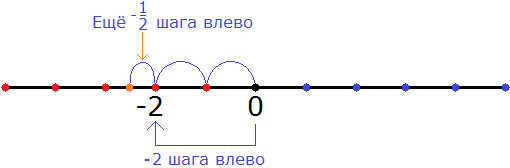
Теперь мы можем понять, почему смешанное число расположилось в левой части координатной прямой. Минус перед двойкой указывает, что мы сдвинулись от нуля на два шага влево, в результате оказались в точке, где находится число −2

Затем, начиная от числа −2 сдвинулись ещё влево на шага. А поскольку значение равно −0,5 то наш шаг будет половиной от полного шага.

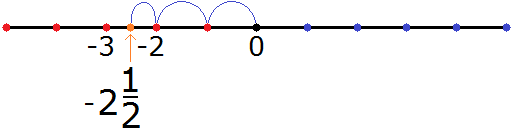
В итоге, мы окажемся посередине между числами −3 и −2

Пример 2. Выделить в неправильной дроби 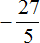целую часть, затем полученное смешанное число обратно перевести в неправильную дробь

Выполним первую часть задания, а именно выделим в неправильной дроби 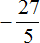целую часть

Выполним вторую часть задания, а именно переведём полученное смешанное число 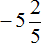в неправильную дробь. Для этого умножим целую часть на знаменатель дробной части и из полученного числа вычтем числитель дробной части:

Если нет желания путаться и привыкать к новому правилу, то можно смешанное число заключить в скобки, а минус оставить за скобкой. Тогда можно будет применить старое доброе правило: умножить целую часть на знаменатель дробной части и к полученному числу прибавить числитель дробной части.

Выполним предыдущее задание этим способом, а именно переведём смешанное число 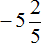в неправильную дробь

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

16 thoughts on “Рациональные числа”

Было бы лучше, чтоб после каждого шага было много задач. Так как без задач, не возможно закрепление и запоминание темы. Только ни в коем случае «один вопрос и пять вариантов ответа». Человек решая, должен быть уверен, что правильно решил задачу.

К каждому шагу дано более одного примера. Вы можете, прочитав условие, самостоятельно попытаться решить примеры.

С большим удовольствием прошёлся по материалу и освежил знания. Жаль нет продолжения. Очень всё доходчиво, спасибо.

Здравствуйте admin! С большим удовольствием повторил математику, скажите пожалуйста какие дальше темы?Очень нужно экспрессом к вышке добраться

Спасибо за сайт с удовольствием изучаю то что пропустил многие годы назад. Но хотелось бы узнать профессию автора и квалификацию и о том дойдет ли админ до разделов высшей математики.

По вашим статьям надо учебники писать. Если бы в у нас в книгах все так понятно писали все бы были отличниками.

Здравствуйте мы продолжаем учится товарищ ленин сказал учиться не поздно а ещё желаю увидеть вышие матиматику в адресе

Источник