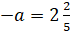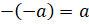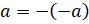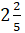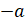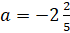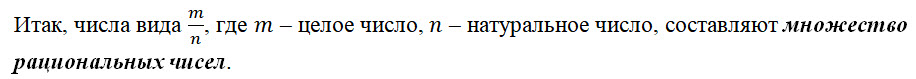Что такое рациональные числа видеоурок
Видеоурок по математике «Целые и рациональные числа»
Число — важнейшее математическое понятие, меняющееся на протяжении веков. Вы уже знаете, что числа, которые мы используем в счёте, называют натуральными. Кстати, натуральные числа — это один из первых математических объектов, который стал изучать человек, так как повседневная жизнь требовала использования натуральных чисел на практике, и, в частности, в счёте. Поэтому и изучение математики в школе мы начинали именно со знакомства с натуральными числами.
С понятием натуральных чисел мы с вами разобрались, а теперь давайте перейдём к действиям с ними. И ответим на вопрос: какие числа получают при сложении и умножении натуральных чисел?
Конечно же, вам не составит труда ответить на этот вопрос. И вы сразу скажете, что при сложении натуральных чисел всегда получают натуральные числа. И при умножении натуральных чисел тоже всегда получают натуральные числа.
Тогда возникает новый вопрос: а какие числа мы получим при вычитании и делении натуральных чисел?
Так вот, при нахождении разности и частного натуральных чисел не всегда получаются натуральные числа. В связи с этим математикам пришлось расширять знания, связанные с числами.
Если мы добавим к натуральным числам нуль и отрицательные числа (то есть числа, которые противоположны натуральным), то множество натуральных чисел расширится до множества целых чисел.
Мы с вами разобрались с понятием целых чисел, а теперь давайте перейдём к действиям с ними. Понятно, что при сложении, вычитании и умножении целых чисел всегда получают целые числа. Чего нельзя сказать о делении целых чисел. При нахождении частного двух целых чисел в результате не всегда получают целые числа.
Следовательно, понятия, связанные с числами, пришлось расширять дальше. Так, множество целых чисел расширили, введя множество рациональных чисел.
Одно и то же рациональное число можно представить различными дробями, которые получаются из несократимой дроби умножением её числителя и знаменателя на одно и то же целое число, отличное от нуля.
Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби. Такие числа можно записать в виде бесконечной десятичной дроби. Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру — её периодом.
Тогда можем сделать такой вывод: любая периодическая дробь — это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр — период дроби.
А теперь давайте приступим к практической части нашего урока.
Видеоурок по математике «Целые и рациональные числа»
Число — важнейшее математическое понятие, меняющееся на протяжении веков. Вы уже знаете, что числа, которые мы используем в счёте, называют натуральными. Кстати, натуральные числа — это один из первых математических объектов, который стал изучать человек, так как повседневная жизнь требовала использования натуральных чисел на практике, и, в частности, в счёте. Поэтому и изучение математики в школе мы начинали именно со знакомства с натуральными числами.
С понятием натуральных чисел мы с вами разобрались, а теперь давайте перейдём к действиям с ними. И ответим на вопрос: какие числа получают при сложении и умножении натуральных чисел?
Конечно же, вам не составит труда ответить на этот вопрос. И вы сразу скажете, что при сложении натуральных чисел всегда получают натуральные числа. И при умножении натуральных чисел тоже всегда получают натуральные числа.
Тогда возникает новый вопрос: а какие числа мы получим при вычитании и делении натуральных чисел?
Так вот, при нахождении разности и частного натуральных чисел не всегда получаются натуральные числа. В связи с этим математикам пришлось расширять знания, связанные с числами.
Если мы добавим к натуральным числам нуль и отрицательные числа (то есть числа, которые противоположны натуральным), то множество натуральных чисел расширится до множества целых чисел.
Мы с вами разобрались с понятием целых чисел, а теперь давайте перейдём к действиям с ними. Понятно, что при сложении, вычитании и умножении целых чисел всегда получают целые числа. Чего нельзя сказать о делении целых чисел. При нахождении частного двух целых чисел в результате не всегда получают целые числа.
Следовательно, понятия, связанные с числами, пришлось расширять дальше. Так, множество целых чисел расширили, введя множество рациональных чисел.
Одно и то же рациональное число можно представить различными дробями, которые получаются из несократимой дроби умножением её числителя и знаменателя на одно и то же целое число, отличное от нуля.
Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби. Такие числа можно записать в виде бесконечной десятичной дроби. Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру — её периодом.
Тогда можем сделать такой вывод: любая периодическая дробь — это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр — период дроби.
А теперь давайте приступим к практической части нашего урока.
Целые числа. Рациональные числа
Урок 31. Математика 6 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Целые числа. Рациональные числа»
Представим себе такую историю…
– Привет, Паша! – поздоровался с другом Саша. – Извини, что опоздал.
– Что случилось? – поинтересовался Паша.
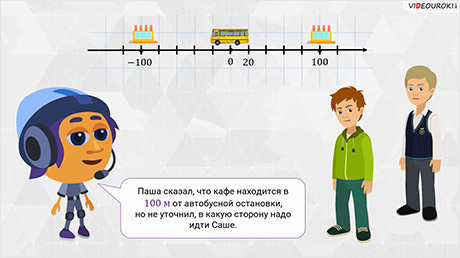
– Ничего не случилось. Просто когда мы договаривались встретиться в кафе, ты сказал, что мне нужно выйти из автобуса и пройти дальше по тротуару 100 метров. Но ты не сказал, в какую сторону надо идти, – говорил немного расстроенный Саша.
– После того, как ты вышел из автобуса, надо было идти дальше по направлению движения автобуса, то есть повернуть налево и пройти 100 метров, – пояснил Паша.
– А я повернул направо и прошёл 100 метров, – сказал Саша.
– Извини, что так вышло. Ты прошёл 100 метров, но в противоположном направлении. А давай мы об этом поговорим с Мудряшом, – предложил другу Паша.
– Давай, – согласился с ним Саша.
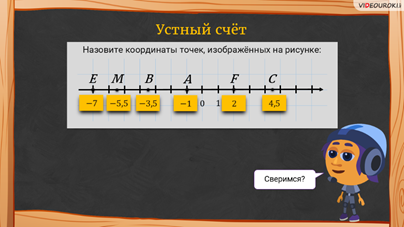
– Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!
– А сейчас можем вернуться к вашему вопросу, – начал Мудряш. – На прошлом уроке мы с вами ввели понятие координатной прямой. Напомним, что координатной прямой называют прямую, на которой выбрали начало отсчёта, единичный отрезок и направление.
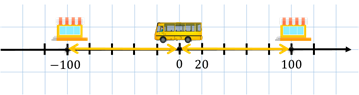
Начертим координатную прямую. Отметим на ней начало отсчёта. Пусть длина единичного отрезка равна 20 метрам. Представим, что автобусная остановка, на которой вышел Саша, расположена в начале отсчёта. Паша сказал Саше, что кафе находится в 100 метрах от автобусной остановки, но не уточнил, в какую сторону нужно идти Саше.
Если бы кафе было расположено справа от автобусной остановки, то есть от начала отсчёта, то на координатной прямой ему бы соответствовала точка 100. А если бы слева, то ему бы соответствовала бы точка 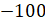
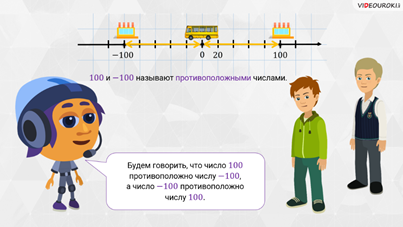
То есть получается, чтобы попасть из начала в эти точки, надо пройти одинаковые расстояния, но в противоположных направлениях. Тогда числа 100 и 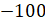
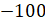
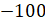
Давайте ещё приведём примеры противоположных чисел.
– 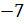
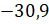
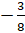

– Запомните! – сказал Мудряш. – Число 0 противоположно самому себе. Число, противоположное числу a, обозначают как 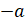
– Обратите внимание, – продолжил Мудряш, – что, поставив, например, перед положительным числом 15 знак «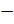
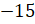
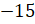
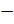
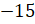
– Запомните! – сказал Мудряш. – Число, противоположное числу 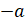
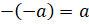
– Получается, что каждое число имеет противоположное ему число? – спросили ребята.
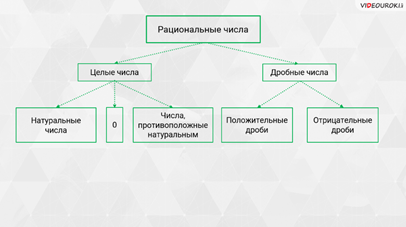
– Да, и только одно, – сказал Мудряш и добавил, – запомните! Все натуральные числа, противоположные им числа и 0 называют целыми числами. Натуральные числа называют целыми положительными числами. А числа, противоположные натуральным, называют целыми отрицательными числами.
– Тогда как называют числа, например, 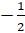
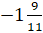
– Такие числа называются дробными числами, – ответил Мудряш. – Запомните! Целые и дробные числа называют рациональными числами.
– Давайте приведём примеры рациональных чисел, – предложил Мудряш.
– 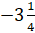
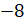
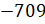

– Хорошо! А сейчас составим следующую схему, – сказал Мудряш. – Мы сказали, что рациональными называют целые и дробные числа. Целыми числами называют натуральные числа, 0 и числа, противоположные натуральным. Дробными числами являются положительные и отрицательные дроби.
А теперь давайте выполним несколько заданий.
Задание первое: найдите числа, противоположные числам 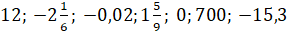
Решение: первое число у нас 12. Припишем перед ним знак «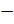
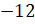
Второе число у нас 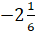
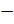
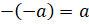
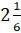
Следующее число у нас 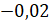
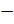
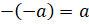
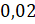
Перед числом 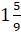
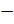
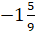
Противоположным числу 0 является само число 0.
Следующее число у нас 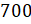
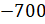
Перед числом 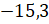
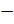
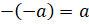
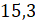
Следующее задание: выберите из чисел 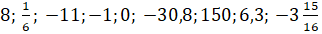
Решение: давайте заполним следующую таблицу.
Число 8 мы можем отнести к натуральным числам, целым и неотрицательным. Напомним, что к неотрицательным числам относятся положительные числа и 0.

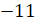
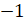
0 отнесём к целым и неотрицательным.
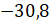
150 запишем к натуральным, целым и неотрицательным.
6,3 отнесём к неотрицательным числам и дробным.
И последнее число у нас 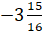
И ещё одно задание: решите уравнения: а) 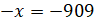
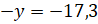
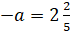
Решение: первое уравнение: 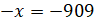
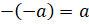
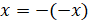
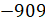
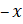
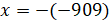
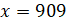
Второе уравнение: 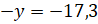
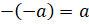
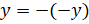
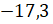
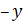
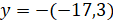
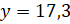
И последнее уравнение: