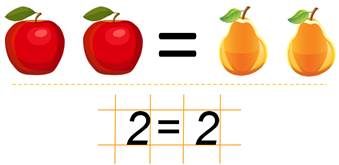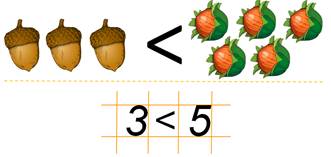Что такое равенство и неравенство 2 класс в математике примеры

«Равенства и неравенства» Уравнения 2 класс

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Равенства и неравенства. Уравнения.

ФИО учителя: Суесенова А.Т.

Цели обучения (ЦО) из долгосрочного плана

Различать равенство, неравенство;

Определять верные и неверные равенства;

Основные термины и словосочетания:

Верное и неверное равенство знаки «больше», «меньше», «равно» ;

Вопросы для обсуждения:

Какой знак используется для обозначения равенства?

Какой знак используется для обозначения неравенства?

Сотрудничество, уважение, образование в течение всей жизни.

Определяет равенство, неравенство; Находит верные, неверные равенства;

Различает верные, неверные равенства, используя знаки «+», «-», « ≠ », «=», «>», « ;

Слайд, карточки с заданиями, интерактивная доска.

Запланированные периоды урока

Я рада видеть ваши лица, ваши улыбки и думаю, что этот день принесёт в ам радость, общение друг с другом. Сядьте удобно, закройте глаза и повторяйте за мной: «Я в школе, я на уроке. Я радуюсь этому. Внимание мое растет. Я как разведчик, все замечу. Память моя крепка. Голова мыслит ясно. Я хочу учиться. Я готов к работе. Я работаю. Молодцы ребята!».

Чтобы узнать тему нашего урока, мы должны решить примеры и расположить числа в порядке возрастания. (Слайд)

Назовите тему нашего урока?

Мы будем составлять и решать равенства и неравенства.

Форма оценивания: Самооценивание по эталону

Дифференциация по способу «Диалог и поддержка» (оказывается помощь учителя учащимся, испытывающим затруднения)

Задание 1 (И) «Подбери примеры!»

Соотнеси равенство и неравенство по кружочкам.

Задание 2. (П) «Расставь знаки»

Поставь знаки «+» или « –».

6 1 7 7 1 > 5 5

7 2= 5 5 1=7 1

7 3 > 9 9 3 1

Критерий: Различает верные неверные равенства используя знаки «+», «-».

Игровое упражнение « Вагончики»

У каждого учащегося карточка с выражением (равенство или неравенство). Перед доской стоят 2 машиниста и держат в руках листочки, на которых написано: «Равенства» и « Н еравенства» Дети читают свое выражение и присоединяются к вагончикам.

Что называется равенством?

Что называе тся неравенством?

(И) Задание 3. «Найди ошибку».

Решите примеры. Найдите ошибки.

Сколько неверных равенств ты нашел?

Критерий: различает верные, неверные равенства.

— находит неверные равенств а ;

Критерий: определяет равенство и неравенство.

-читает задачу и составляет краткую запись

-составляет выражение со знаком «-»

Мы решали, мы решали.

Что-то очень мы устали.

Мы сейчас потопаем,

Улыбнемся, тихо сядем.

Задание уровня А: Соединить стрелками числовые и буквенные выражения, равенства и неравенства

3+5 > 6 числовое выражение

Критерий: находит верные, неверные равенства;

-соотносит выражение со словом «равенство»

-соотносит выражение со словом «неравенство»

-соотносит выражение со словом «буквенное выражение»

— соотносит выражение со словом « числовое выражение

Задание уровня В: Зачеркни неверные равенства.

Критерий: находит неверные равенства;

Задание уровня С: Сравните значения числовых выражений, определите их вид .

Критерий: определяет равенство, неравенство;

Источник

Понятие равенства, знак равенства, связанные определения

Материал статьи позволит ознакомиться с математической трактовкой понятия равенства. Порассуждаем на тему сути равенства; рассмотрим его виды и способы его записи; запишем свойства равенства и проиллюстрируем теорию примерами.

Что такое равенство

Само понятие равенства тесно переплетено с понятием сравнения, когда мы сопоставляем свойства и признаки, чтобы выявить схожие черты. Процесс сравнения требует наличия двух объектов, которые и сравниваются между собой. Данные рассуждения наводят на мысль, что понятие равенства не может иметь место, когда нет хотя бы двух объектов, чтобы было что сравнивать. При этом, конечно, может быть взято большее количество объектов: три и более, однако, в конечном, счете, мы так или иначе придем к сравнению пар, собранных из заданных объектов.

Смысл понятия «равенство» в обобщенном толковании отлично определяется словом «одинаковые». О двух одинаковых объектах можно говорить – «равные». Например, квадраты и . А вот объекты, которые хоть по какому-то признаку отличаются друг от другу, назовем неравными.

Говоря о равенстве, мы можем иметь в виду как объекты в целом, так и их отдельные свойства или признаки. Объекты являются равными в целом, когда одинаковы по всем характеристикам. Например, когда мы привели в пример равенство квадратов, имели в виду их равенство по всем присущим им свойствам: форме, размеру, цвету. Также объекты могут и не быть равными в целом, но обладать одинаковыми отдельными признаками. Например: и . Указанные объекты равны по форме (оба – круги), но различны (неравны) по цвету и размеру.

Таким образом, необходимо заранее понимать, равенство какого рода мы имеем в виду.

Запись равенств, знак равно

Равенство – запись, в которой использован знак равно, разделяющий два математических объекта (или числа, или выражения и т.п.).

Верные и неверные равенства

Составленные равенства могут соответствовать сути понятия равенства, а могут и противоречить ему. По этому признаку все равенства классифицируют на верные равенства и неверные равенства. Приведем примеры.

Свойства равенств

Запишем три основных свойства равенств:

Буквенно сформулированные свойства запишем так:

Отметим особенную пользу второго и третьего свойств равенств – свойств симметричности и транзитивности – они дают возможность утверждать равенство трех и более объектов через их попарное равенство.

Двойные, тройные и т.д. равенства

При помощи таких цепочек равенств оптимально составлять равенство трех и более объектов. Такие записи по своему смыслу являются обозначением равенства любых двух объектов, составляющих исходную цепочку равенств.

Составляя подобные цепочки, удобно записывать последовательность решения примеров и задач: такое решение становится наглядным и отражает все промежуточные этапы вычислений.

Источник

Равенство и неравенство. Знаки: больше, меньше, равно

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Математические знаки

Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.

Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:

Символ меньше (

Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:

Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:

Равенство и неравенство

Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.

Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».

Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.

Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:

Типы неравенств

Источник

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Знаки: «>» больше, «

Однажды решили Белочка и Ёжик проверить, что птицы любят есть больше всего: пшеничные зерна или крошки белого хлеба. На один пень насыпали зерна, а на другой крошки хлеба и стали наблюдать.

— Ежик, ну что ты там видишь?

— О, теперь вижу. Два воробья прилетели. Сейчас зерна будут клевать.

— Ой. Ко второму пню, ну там где крошки, сорока наша прилетела.

— Так где птиц больше?

— На пне с зернышками птиц больше, чем около пня с крошками.

— Белочка, кажется дядя Филя прилетел.

— Ну, и где сейчас птиц стало больше?

— Теперь птиц стало одинаково.

— Любик, а ты знаешь, что в математике, чтобы сравнивать объекты или предметы используют специальные математические знаки: больше, меньше и равно.

Например, вот у нас одно яблоко и одна груша, т.е. яблок столько же сколько и груш. Значит между ними можно поставить знак равно. А записать это можно так: два равно двум.

Теперь мы сравним грибы: три боровика и две лисички. Что больше?

— Три боровика больше, чем две лисички.

— Правильно. В этом случае мы между грибами поставим знак больше. А записать это можно так: три больше чем два.

— А сейчас сравним жёлуди и орехи. Чего меньше?

— Ага… Желудей у нас три, а орехов пять. Значит желудей меньше, чем орехов.

— Правильно, в этом случае мы поставим знак меньше. А записать это можно так: пять меньше чем три.

А теперь мы посмотрим, как пишутся эти знаки.

— Я помню как пишется знак равно. Он состоит из двух палочек, которые пишутся друг под другом. Вот.

— Правильно. Знаки больше и меньше тоже состоят из двух палочек. В знаке больше палочки расходятся к большему числу, а записывается этот знак так.

В знаке меньше палочки сходятся к меньшему числу и записывается он так.

— Ежик, допиши пожалуйста знаки в строчку, в пустые клеточки.

— Ага… Сейчас, сейчас. Сначала допишу знак равно, теперь больше и меньше.

А чтобы ты не запутался, запомни: левая рука, согнутая в локте даст нам знак меньше, а правая рука согнутая в локте даст нам знак больше.

Если между двумя числами поставить знак равно, то получится числовое равенство. А если между двумя числами поставить знаки больше или меньше, то получится числовые неравенства.

Ежик, а теперь проверь пожалуйста, верные ли равенства и неравенства.

Так, так, так. Ага. Два больше чем один – все верно, три больше, чем четыре…ага…

что-то не так, три обозначает большее количество предметов, чем четыре и при счете

идет раньше, чем четыре значит это неравенство не верное. Мы его зачеркнем.

— А давай лучше исправим, чтобы у нас не было ошибок.

— Давай. Значит здесь надо поставить знак меньше. Вот.

— Так-так. Пять равно пяти. Все верно.

— Ага, а здесь совсем сложно.

— Ничего сложного. Смотри, чтобы проверить, надо сначала посчитать, сколько будет два да один.

— А сколько будет два да три.

— Пять. Значит три меньше пяти. Здесь опять ошибка. Надо поставить знак меньше.

— Ну молодец Ежик. Ты все правильно выполнил. Итак, ты должен запомнить:

1. Чтобы сравнить числа в математике используют знаки больше, меньше или равно.

2. Знак больше, расходится палочками к большему числу. И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство.

3. Знак меньше, сходится палочками к меньшему числу. И если согнуть левую руку в локте, то получится знак меньше. Выражение, в котором стоит знак меньше тоже называется неравенство.

4. Знак равно состоит из двух палочек, которые пишутся друг под другом, а выражение, в котором стоит знак равно называется числовым равенством.

— Белочка, а давай посмотрим, что там наши птицы делают?

— Все склевали и улетели. Да, теперь мы не сможем определить, что же птицы любят больше. Ничего не осталось.

— Наверное, Ежик, одни птицы больше любят есть зерна, а другие хлебные крошки.

Источник

Конспект урока по математике на тему «Закрепление изученного: равенства и неравенства» (2 класс)

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

равенства и неравенства Предмет: математика

Образ урока: задание классификации познаний и умений

Задача урока: обобщить и классифицировать познания ребят по теме «Целое и части».

• Закрепить связь поступков на базе мнений «целое» и «части»

• закрепить изученные вычислительные приёмы склады и вычитания, внедрение учениками приобретённых познаний и умений в практической работы.

• повторить очередность количеств в границах 20;

• развивать математическую речь, аристократия собственно что это «целое» и «части», наименования компонент и итогов поступков склады и вычитания;

• развивать психологические процессы: забота, память, мышление, фантазия, эмоции;

• развивать опыт самооценивания;

• воспитывать энергичность, усидчивость, прилежание в процессе учения

составление умения избирать более действенные методы заключения задач в зависимости от условий;

составление методик и критерий воздействия, контроль и оценка процесса и итогов деятельности;

составление умения разбирать немаловажные и несущественные признаки;

составление умения ставить причинно-следственные связи;

составление умения возводить закономерную цепочку размышления.

составление волевой саморегуляции, как дееспособность к преодолению преград, к мобилизации сил и энергии;

формирование умения давать своим действиям самооценку;

формирование умения ставить учебную задачу;

формирование умения осуществлять способы действия с заданным эталоном;

формирование умения планировать свои действия с учётом поставленной цели;

формирование умения рефлексировать свои действия, контролировать и оценивать результаты своей деятельности.

формирование умения планировать учебное сотрудничество;

формирование умения слушать и слышать;

формирование умения построения речевых высказываний.

развитие доверия друг к другу, готовности к сотрудничеству.

У р о к 61. Закрепление изученного:
равенства и неравенства

Цели: повторить с учащимися понятия «равенство», «неравенство»; развивать вычислительные навыки, мышление учеников.

I. Организационный момент.

II. Каллиграфическая минутка.

2. Какое число пропущено?

3. Вставьте знаки арифметических действий «+» или «–» так, чтобы равенства были верными.

IV. Повторение понятий «равенство», «неравенство».

15 + 5 = 28 – 8 9 + 4 > 14 – 6

1 м = 10 дм 2 м > 20 см

– Рассмотрите внимательно записи на доске.

– Чем похожи записи каждого столбика?

– Как называется запись, в которой есть знак «=»? (Равенство.)

– Как называется запись, в которой есть знаки «>», «

– Составьте верные равенства и неравенства, используя выражения:

6 + 8, 17 – 10, 24 – 10, 37 – 30.

V. Сравнение выражений.

На данном этапе урока учащимся может быть предложено задание 6 (с. 76 учебника, часть 1), которое они выполняют с устным объяснением, а затем в качестве самостоятельной работы – задание по карточкам.

VI. Решение выражений.

1. Учащиеся выполняют с подробным устным объяснением задание 2 (с. 76 учебника, часть 1), в котором находят значения данных выражений, а затем проверяют их.

После этого выполняется задание 8 (с. 76 учебника, часть 1). Задание может быть выполнено следующим образом: дети рассматривают выражения первого столбика и приходят к выводу о том, что для решения выражений необходимо воспользоваться приёмом группировки слагаемых, данный столбик выполняется с комментированием.

З а п и с ь в тетради:

40 + 7 + 3 + 18 = 40 + (7 + 3) + 18 = 40 + 10 + 18 = 50 + 18 = 68

50 + 26 + 8 + 2 = 50 + 26 + (8+ 2) = 50 + 10 + 26 = 60 + 26 = 86

30 + 9 + 6 + 1= 30 + (9 + 1) + 6 = 30 + 10 + 6 = 40 + 6= 46

Далее учитель предлагает ученикам рассмотреть выражения второго столбика.

– Чем интересны выражения этого столбика?

– Как, по вашему мнению, будут изменяться значения данных выражений?

2. Групповая работа.

В качестве групповой работы учащимся могут быть предложены задания 1, 3 (с. 76 учебника, часть 1).

Выполняя задание 1, дети находят ошибки и исправляют их. В задании 3 ставят скобки таким образом, чтобы записи были верными.

VII. Задание на смекалку.

Учащиеся выполняют задание на с. 76 учебника (часть 1), в котором заполняют таблицу. (Вторая строка – в зелёном квадрате красный круг, в синем треугольнике красный круг, в жёлтом прямоугольнике красный круг, в белом круге красный круг; третья строка – в зелёном квадрате чёрный треугольник, в синем треугольнике чёрный треугольник, в жёлтом прямоугольнике чёрный треугольник, в белом круге чёрный треугольник.)

– Что хотите сказать?

– Какие понятия, правила повторяли сегодня на уроке?

– Как вы сегодня работали?

– Что бы хотели выполнить ещё?

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Конспект урока по математике на тему «Работа над задачами и уравнениями» ( 2 класс)

Конспект урока по математике на тему «Проверка вычитания» (2 класс)

Конспект урока по математике на тему «Проверка сложения» ( 2 класс)

Методическая разработка на тему: «Формы и методы обучения на современном учебном занятии по математике»

Презентация по математике по теме «НАШ ПОСЕЛОК В ЧИСЛАХ И ВЕЛИЧИНАХ» 4 класс

Конспект урока по математике на тему «Деление на 3. Закрепление» (2 класс)

Конспект урока по математике 1 класс тема» Прямоугольник»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5373172 материала.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил разработать концепцию развития допобразования детей до 2030 года

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Госдума приняла закон об использовании онлайн-ресурсов в школах

Время чтения: 2 минуты

Трехлетнюю олимпиаду среди школ запустят в России в 2022 году

Время чтения: 1 минута

В России утверждены новые аккредитационные показатели для школ и колледжей

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник