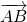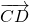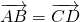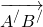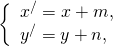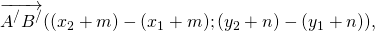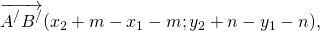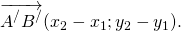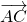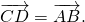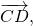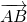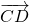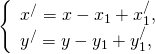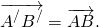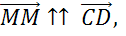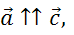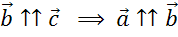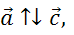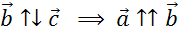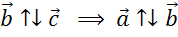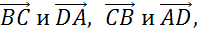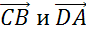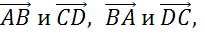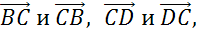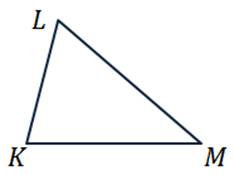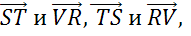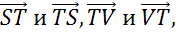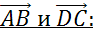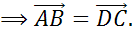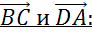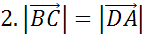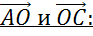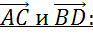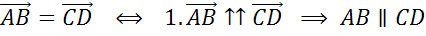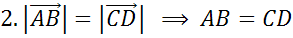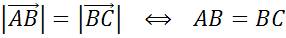Что такое равенство векторов
Равные векторы
В различных школьных учебниках определение равных векторов даётся по-разному.
В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.
Два вектора называются равными, если они совмещаются параллельным переносом.
(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Равенство векторов обозначают так:
(Свойства равных векторов)
1) Равные векторы сонаправлены и имеют равные длины.
2) Равные векторы имеют равные координаты.
3) От любой точки можно отложить вектор, равный данному, и притом только один.
1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.
2) Пусть дан вектор
с началом в точке A(x1; y1) и концом в точке B(x2; y2).
По определению равных векторов, вектор
равный данному, получен из
Если этот параллельный перенос задан формулами
Найдём координаты каждого из векторов:
То есть координаты равных векторов
Что и требовалось доказать.
Таким образом, координаты задают длину и направление вектора, но не фиксируют его.
3) Пусть даны вектор
и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор
При таком параллельном переносе вектор
переходит в вектор
По определению равных векторов,
Что и требовалось доказать.
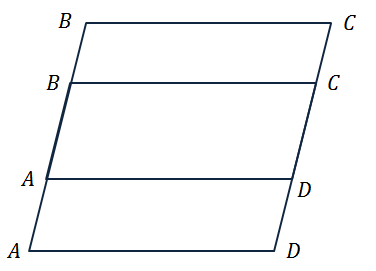
На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).
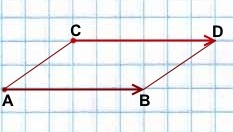
отложенный от точки C, равен вектору
(Признаки равенства векторов)
1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.
2) Если у векторов соответствующие координаты равны, то векторы равны.
1) 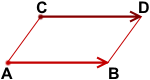
сонаправлены и имеют одинаковые длины.
Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор
переводит в вектор
По определению равных векторов,
Что и требовалось доказать.
Параллельный перенос, заданный формулами
переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы
А это означает, что
Что и требовалось доказать.
В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.
Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.
Равенство векторов
Урок 2. Геометрия 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Равенство векторов»
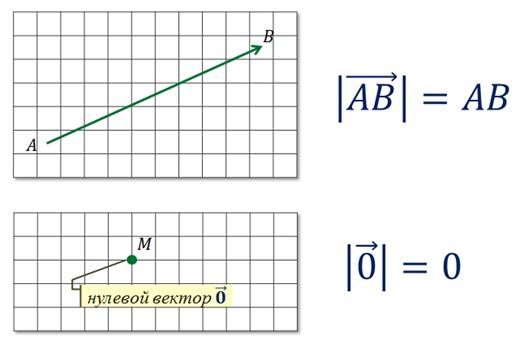
Вы уже знакомы с понятием вектора, знаете, что каждый вектор характеризуется направлением и длиной, которая равна длине соответствующего отрезка.
Также с прошлых уроков вам известно, что любая точка плоскости тоже является вектором, нулевым вектором. Длина нулевого вектора всегда равна нулю.
Обладая всеми этими знаниями, мы можем приступить к изучению равных векторов.
Но перед этим введём понятие коллинеарных векторов.
Ненулевые векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
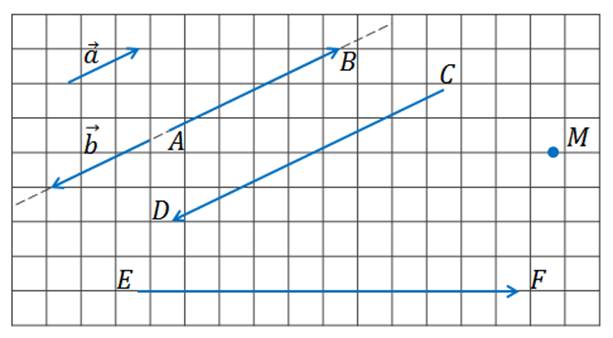
Посмотрим на рисунок и найдём на нём коллинеарные векторы.
Векторы 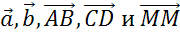
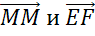
А вот, например, векторы 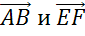
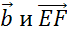
Рассмотрим два коллинеарных вектора 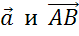
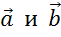
Запомните, в первом случае векторы называют сонаправленными и обозначают их таким знаком 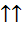
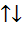
Если говорить о нулевом векторе, то стоит вспомнить, что его начало совпадает с концом. Поэтому он не имеет какого-то определённого направления. Другими словами, любое направление можно считать направлением нулевого вектора. Поэтому нулевой вектор будет сонаправлен с любым вектором. Например, векторы 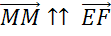
Для ненулевых коллинеарных векторов можно выделить следующие свойства.
Если вектор 
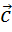

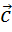


Если вектор 
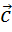

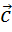


Если вектор 
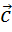

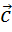


Итак, мы ввели понятие коллинеарных векторов. Узнали, какие векторы называются сонаправленными, а какие — противоположно направленными.
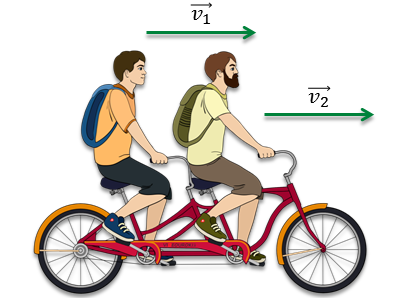
А теперь рассмотрим такой пример. На велосипеде-тандеме едут два туриста. Каждый из них движется в одном и том же направлении и с одной и той же скоростью.
Скорость каждого туриста является векторной величиной, и мы можем изобразить её в виде вектора.
Так как направления движения совпадают и скорости равны, то векторы будут иметь одинаковые направления и равные длины.
Этот пример даёт нам понять, как дать определение равным векторам.
Векторы называют равными, если они сонаправлены и их длины равны.
Равенство векторов обозначают так 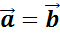
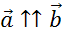
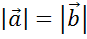
Приступим к решению задач.
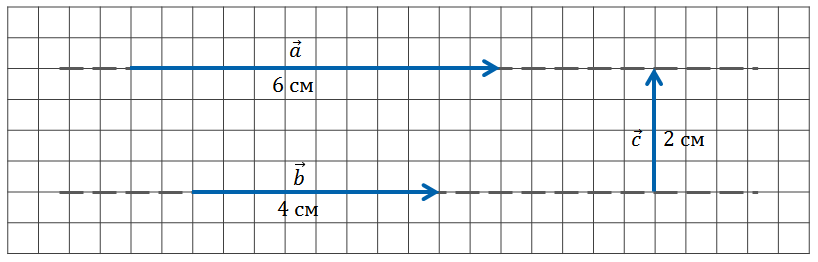
Задача. Начертить векторы 

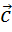


а векторы 
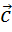


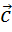
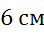
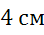
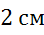
Чтобы векторы 



Вектор 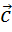

Перейдём к следующей задаче.
Задача. Выписать пары коллинеарных векторов, которые определяются сторонами:
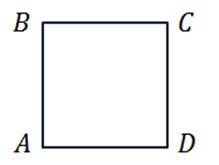
а) квадрата 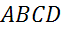
б) треугольника 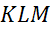
в) трапеции 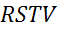
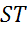
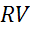
Изобразим квадрат ABCD. Коллинеарные векторы лежат на одной прямой или на параллельных прямых.
Рассмотрим параллельные стороны BC и АD. Можем записать такие пары коллинеарных векторов: 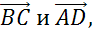
Рассмотрим параллельные стороны AB и CD. Можно записать следующие пары коллинеарных векторов: 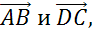
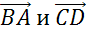
Также коллинеарными будут векторы 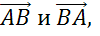
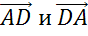
Получили 12 пар коллинеарных векторов.
В следующем пункте изобразим треугольник KLM.
Никакие из его сторон не параллельны. Но коллинеарными будут векторы, лежащие на одной стороне: 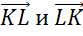
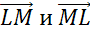
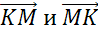
Получили 3 пары коллинеарных векторов.
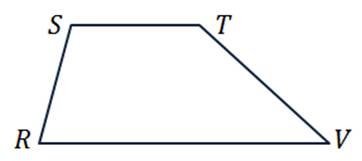
В последнем пункте изобразим трапецию PSTV так, чтобы стороны ST и PV являлись её основаниями.
Параллельных сторон видим только две, поэтому запишем следующие пары коллинеарных векторов: 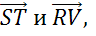
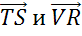
Также коллинеарными будут векторы, лежащие на одной стороне: 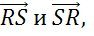
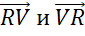
Получили 8 пар коллинеарных векторов.
Рассмотрим следующую задачу.
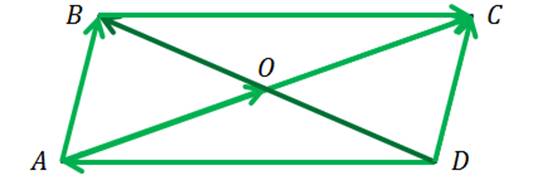
Задача. Диагонали параллелограмма 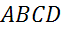
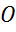
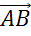
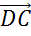
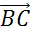
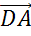
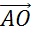
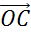
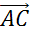
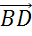
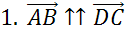
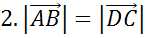
Следующая пара векторов
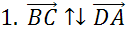
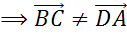
Далее обратим внимание на пару векторов
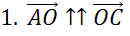
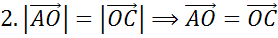
Последней рассмотрим пару векторов
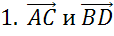
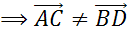
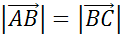
Задача. Определить вид четырёхугольника 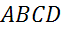
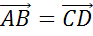
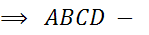
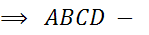
Подведём итоги урока.
Сегодня мы познакомились с понятием коллинеарных векторов. Так называют ненулевые векторы, которые лежат на одной прямой либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
При этом среди коллинеарных векторов мы выделили два случая: сонаправленные векторы (они имеют одинаковое направление) и противоположно направленные векторы (они имеют противоположные направления).
Опираясь на эти знания, мы дали определение равным векторам.
Векторы называют равными, если они сонаправлены и их длины равны.
Эти знания очень важны, они пригодятся вам при решении задач и при дальнейшем изучении векторов.