Что такое равное слагаемое
Подобные слагаемые, их приведение, примеры
Приведение подобных слагаемых является одним из наиболее употребимых тождественных преобразований. В этом разделе мы дадим определение термина, разберем, что обозначает словосочетание «приведение подобных слагаемых», рассмотрим основные правила выполнения действий и наиболее распространенные типы задач.
Определение и примеры подобных слагаемых
В большинстве учебных пособий тема подобных слагаемых разбирается после знакомства с буквенными выражениями, когда появляется необходимость проводить с ними различные преобразования.
Подобные слагаемые – это слагаемые, которые имеют одинаковую буквенную часть.
Слагаемые – это, как известно, составные элементы суммы. Это значит, что они могут присутствовать лишь в тех выражениях, которые представляют собой сумму. Буквенная часть – это одна или произведение нескольких букв, которые представляют собой переменные. Слагаемые с буквенной частью – это произведение некоторого числа и буквенной части. Здесь некоторое число также носит название числового коэффициента.
Буквенная часть может быть представлена не только произведением букв, но также и произвольным буквенным выражением. Например:
Обобщим изложенные выше утверждения и дадим еще одно определение подобных слагаемых.
Подобные слагаемые – это слагаемые в буквенном выражении, которые имеют одинаковую буквенную часть, а также слагаемые, которые не имеют буквенной части, если под буквенной частью понимать любое буквенное выражение.
Числовые коэффициенты подобных слагаемых могут быть равны, тогда мы говорим о том, что подобные слагаемые одинаковые. Если же числовые коэффициенты различаются, то подобные слагаемые будут разными.
Возьмем для примера выражение 2 · x · y + 3 · y · x и рассмотрим такой нюанс: являются ли слагаемые 2 · x · y и 3 · y · x подобными. В задачах этот вопрос может иметь следующую формулировку: одинаково ли буквенное выражение части x · y и y · x указанных слагаемых? Буквенные множители в приведенном примере имеют различный порядок, что в свете данного выше определения не делает их подобными.
К слову, в некоторых источниках при нестрогом отношении к вопросу, слагаемые из примера могут называться подобными. Но лучше не допускать таких неточностей в трактовках.
Приведение подобных слагаемых, правило, примеры
Под преобразованием выражений, которые содержат подобные слагаемые, подразумевается проведение сложения этих слагаемых. Проводится это действие обычно в три этапа:
Приведем пример таких вычислений.
Описанные три шага для экономии времени записывают в виде правила приведения подобных слагаемых. Согласно правило для того, чтобы привести подобные слагаемые, необходимо сложить их коэффициенты, а затем умножить полученный результат на буквенную часть при ее наличии.
Решение
Что такое равное слагаемое
Числа – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т.д.).
Для записи чисел используются специальные знаки – цифры.
1 2 3 4 5 6 7 8 9 0
Числа, которые используются при счёте, называются натуральными.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …, □
1 – самое маленькое число.
□ – самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль не является натуральным число.
Из двух натуральных чисел больше то, которое в натуральном ряду расположено правее, а меньше то, которое расположено левее:
Из двух натуральных чисел с разным количеством разрядов больше то число, в котором разрядов больше.
Из двух натуральных чисел с одинаковым количеством разрядов больше то, у которого больше цифра старшего разряда.
45 861 47 361 47361 > 45 681
Сложение – это математическое действие.
Числа, которые складываются, называются слагаемыми.
Результат сложение называется суммой.
первое слагаемое второе слагаемое сумма
Если одно из слагаемых равно 0, сумма равна второму слагаемому:
Если оба слагаемых равны 0, то и сумма равна 0: 0 + 0 = 0
Вычитание – действие, обратное сложению.
уменьшаемое вычитаемое разность
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
Переместительный закон сложения.
От перемены мест слагаемых значение суммы не меняется:
Сочетательный закон сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел или ко второму числу прибавить сумму первого и третьего чисел:
(a + b) + c = a + (b + c) = (a + c) + b
(2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4
Умножение – это сложение одинаковых слагаемых.
3 – число, которое показывает, сколько раз повторяется слагаемое 2 (по два три раза)
первый множитель второй множитель произведение
Деление – это действие, обратное умножению.
делимое делитель частное
Переместительный закон умножения.
От перестановки множителей произведение не меняется:
Сочетательный закон умножения.
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел или второе число умножить на произведении первого и третьего чисел:
(2 · 4) · 8 = 2 · (4 · 8) = (2 · 8) · 4
Распределительный закон умножения.
Произведение суммы на число равно сумме произведений каждого слагаемого на это число.
(a + b + c) · d = a · d + b · d + c · d
( 2 + 5 + 3 ) · 2 = 2 · 2 + 5 · 2 + 3 · 2 = 20
Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.
Чтобы разделить сумму на число, достаточно разделить каждое слагаемое на это число, а полученные результаты сложить.
Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе частное.
Частное от деления произведений двух множителей на число равно произведению одного из множителей на частное от деления второго множителя на это число.
(a · b) : c = (a : c) · b = a · (b : c)
Чтобы разделить число на частное, достаточно разделить это число на делимое и полученный результат умножить на делитель.
Чтобы разделить частное на число, достаточно умножить делитель на это число и разделить делимое на полученный результат
Можно так же разделить делимое на это число, а полученный результат разделить на делитель.
НАХОЖДЕНИЕ КОМПОНЕНТОВ ДЕЛЕНИЯ.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
ОСОБЫЕ СЛУЧАИ УМНОЖЕНИЯ.
ОСОБЫЕ СЛУЧАИ ДЕЛЕНИЯ.
На нуль делить НЕЛЬЗЯ!
Нуль можно делить на любое число, получится 0.
На 2 делятся все чётные числа, то есть числа, которые оканчиваются цифрами 0, 2, 4, 6, 8.
На 3 делятся все числа, сумма цифр которых делится на 3.
На 5 делятся все числа, которые оканчиваются на 0 или 5.
На 6 делятся числа, которые делятся одновременно и на 2, и на 3.
На 9 делятся числа, сумма цифр которых делится на 9.
Именованные числа – это числа, полученные при измерении величин и сопровождающиеся названием единиц измерения.
Например: 2 кг, 4 см, 8 л
Именованные числа бывают простые и составные.
Простые именованные числа: 7 м, 18 т, 21 кг – в них входит только одн единица измерения.
Составные именованные числа: 2 м 4 см, 24 кг 45 г, 8 км 520 м – в них входят несколько единиц измерения.
ПРЕОБРАЗОВАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Чтобы перейти от одних единиц измерения к другим, пользуйся таблицей величин.
Единицы измерения длины
1 м = 10 дм = 100 см = 1000 мм
1 км = 1000 м = 10000 дм = 100000 см
Единицы измерения массы
1 т = 10 ц = 1000 кг
Единицы измерения времени
1 ч = 60 мин = 3600 с
1 месяц = 30 или 31 день (в феврале 28 или 29 дней)
1 год = 12 месяцев = 52 недели = 365 или 366 дней
1 век (столетие) = 100 лет
Единицы измерения площади
1 м 2 = 100 дм 2 = 10000 см 2
1 км 2 = 1000000 м 2
1 ар (1 а) = 1 сотка = 100 м 2
1 гектар (1 га) = 10000 м 2
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Складывать и вычитать можно именованные числа, выраженные в одинаковых единицах измерения.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
При умножении и делении составные именованные числа сначала заменяют простыми, а затем выполняют вычисления. В ответе простое именованное число заменяют составным.
Математическое выражение – это фраза, записанная с помощью чисел, знаков и букв.
Выражение, записанное только с помощью чисел и знаков, называется числовым.
Выражение, в котором кроме чисел и знаков есть буквы, называется буквенным.
Любое числовое выражение имеет значение. Найти значение числового выражения – значит найти его ответ.
ПОРЯДОК ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ.
В выражениях без скобок, где выполняются только сложение и вычитание, действия выполняются в том порядке, в котором они записаны (то есть слева направо).
В выражениях без скобок, где выполняются только умножение и деление, действия выполняются в том порядке, в котором они записаны.
В выражениях со скобками первым выполняется действие в скобках, затем умножение или деление и только потом сложение или вычитание.
Уравнение – это равенство, которое содержит в себе неизвестное (переменную), значение которого нужно найти, чтобы равенство было верным.
Решить уравнение – значит найти все значения переменной, при которых уравнение превращается в верное равенство.
РЕШЕНИЕ ПРОСТЕЙШИХ УРАВНЕНИЙ.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, нужно к вычитаемому прибавить разность.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
УЧИМСЯ РЕШАТЬ ЗАДАЧИ.
Как работать над задачей.
1. Прочитай внимательно условие задачи и представь то, о чём идёт речь.
2. Запиши кратко задачу или сделай к ней рисунок, схему, чертёж.
3. Объясни, что означает каждое число.
4. Устно составь план решения задачи.
5. Реши задачу и найди ответ.
6. Проверь решение, составив обратную задачу.
Сумма разрядных слагаемых
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сумма разрядных слагаемых
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:
35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.
30 — разрядное слагаемое; 5 — разрядное слагаемое.
86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86
80 — разрядное слагаемое; 5 — разрядное слагаемое.
356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.
300, 50, 6 — разрядные слагаемые.
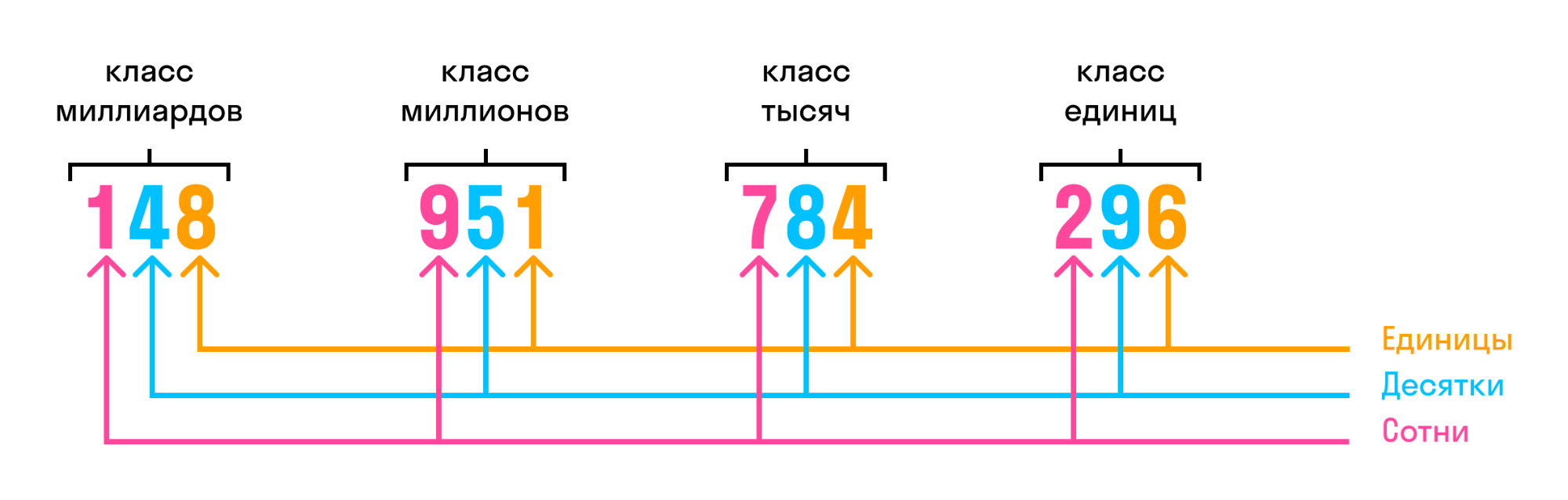
Разряды и классы чисел
Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.
Названия классов многозначных чисел:
Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:
Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.
Разряд — это место, которое занимает цифра в записи многозначного числа.
Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.
Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.
Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.
Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.
Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.
Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.
Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.
Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.
В такой ситуации можете выполнить подробный разбор числа.
Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть
6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.
Из чего состоит это число? Из:
Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.
Определите, сколько единиц в числе 5 068 252.
1. Определяем сколько всего единиц в числе.
2. Определяем количество десятков.
Записываем число без первого разряда (единицы).
3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).
4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).
5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).
6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.
7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.
Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).
Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.
Примеры
Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.
Представьте в виде суммы разрядных слагаемых:
Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.
Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.
Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
2 + 3 = 5
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Урок 42 Бесплатно Подобные слагаемые
В одном из прошлых уроков мы узнали и разобрали одно важное свойство распределительных чисел: распределительное свойство умножения относительно сложения.
Сегодня мы подробно посмотрим, как оно позволяет нам раскрывать скобки и приводить подобные слагаемые, а также в целом упрощать выражение.
Раскрытие скобок
Распределительное свойство умножения справедливо для любых чисел a, b и c.
Также мы уже упоминали, что это свойство можно обобщить, во-первых, для большего числа слагаемых, во-вторых, в роли общего множителей могут выступать не только числа, но и выражения.
Сейчас подробно посмотрим на примерах.
Пример:
Посмотрим на выражение \(\mathbf<(\frac<15><37>+\frac<19><74>)\cdot74>\)
Мы можем сначала посчитать выражение в скобках, а можем сначала раскрыть скобки, избавившись от дробей, а затем выполнить сложение.
Воспользуемся вторым способом:
В данном случае мы имели выражение, максимально близкое к тому, что мы видим в формулировке распределительного свойства.
Теперь рассмотрим такое выражение: \(\mathbf<(1001-65):13>\)
Тут мы видим вычитание вместо сложения и деление вместо умножения.
Но мы уже умеем заменять вычитание на сложение, заменяя вычитаемое на слагаемое, противоположное вычитаемому:
Также и деление мы умеем заменять на умножение, заменяя делитель на множитель, обратный делителю:
Теперь мы получили выражение, соответствующее формулировке распределительного свойства.
Применим же свойство и найдем значение выражения.
Заметим, что хоть мы и заменяли вычитание на сложение, в конце мы все равно вычитали.
Также несмотря на то, что мы заменяли деление на умножение, в конце мы все равно делили.
Распределительное свойство также работает и в таком виде:
Также важно понимать, что распределительное свойство может работать не только с двумя числами, но и с любым другим их количеством.
Три точки обозначают любое количество слагаемых от нуля до бесконечности.
Аналогично предыдущему примеру, слагаемые в скобках могут быть с разными знаками. В таком случае они будут с такими же знаками и в правой части равенства.
Пример:
Раскроем скобки в выражении \(\mathbf<(a+b+c+d)\cdot x>\) :
Также важно понимать, что на месте a, b и других букв в скобках могут стоять любые другие выражения.
Пример:
Также и множитель снаружи скобок может быть не только числом или скобкой, а любым другим выражением, например, как в этом примере ax и bx являются произведениями двух множителей.
Как мы сказали, множитель может быть любым выражением, например, выражением в скобках. Рассмотрим еще такой пример.
Пример:
Раскроем скобки в выражении \(\mathbf<(a+b)(c+d)>\) :
Тут можно действовать в любом порядке: можно считать первую скобку общим множителем, раскрывая вторую, а можно и наоборот.
Мы будем сейчас раскрывать вторую скобку, то есть (\(\mathbf
Теперь общими множителями для первой и второй скобок будут с и d соответственно:
Промежуточный шаг можно было пропустить, так как скобки не несли в нем смысла, но оставим его здесь для наглядности.
Пройти тест и получить оценку можно после входа или регистрации
Вынесение общего множителя
Распределительное свойство умножения относительно сложения помогает нам выносить общий множитель, то есть, смотря на формулировку, мы из правой части переходим в левую.
Сразу скажем, что по аналогии с раскрытием скобок, мы не должны пугаться вычитания и деления, а должны, если сомневаемся, заменять их на сложение и умножение соответственно.
Пример:
Вынесем общий множитель в выражении \(\mathbf
Мы видим, что выражение состоит из трех слагаемых, каждое из которых является произведением.
В каждом из этих произведений есть множитель а.
Его мы и будем выносить.
В данном случае не стояла задача раскрывать скобки. Мы это сделали, чтобы ответ выглядел более законченным
Также можно выносить несколько множителей одновременно.
Пример:
Вынесем общие множители в выражении \(\mathbf
В данном случае в выражении три произведения, в каждом из которых есть множитель а и с, вынесем их:
Кстати, всегда можно проверить себя, раскрыв скобки и убедившись в равенстве полученного выражения и исходного.
Как мы уже сказали, в роли множителей могут выступать всевозможные выражения, а не только числа или произведения. Покажем на примере.
Пример:
Вынесем общие множители в выражении \(\mathbf
Мы видим, что общий множитель есть у первых двух слагаемых и у вторых двух соответственно, вынесем их.
Получается, что выражение состоит из двух слагаемых, каждое из которых является произведением, и в каждом из этих произведений есть множитель \(\mathbf<(a+b>\), вынесем его:
Так мы получили ответ.
Пройти тест и получить оценку можно после входа или регистрации
Приведение подобных слагаемых
В заголовке мы упомянули два новых термина, поэтому сначала дадим им определения.
Подобными слагаемыми называют такие слагаемые, которые имеют одинаковую буквенную часть.
Пример:
Посмотрим, какие есть подобные слагаемые в выражении \(\mathbf<12ab+2b+3ab+5\frac<1><2>b+0.2b>\)
У первого и третьего слагаемого буквенная часть равна \(\mathbf
У второго, четвертого и пятого слагаемого буквенная часть равна \(\mathbf\), эти три слагаемых являются подобными.
Если же мы зададимся вопросом, являются ли подобными первые два слагаемых, то ответ будет отрицательным.
В самом деле, их буквенные части отличаются: \(\mathbf
Внимательный читатель заметит, иногда \(\mathbf
Нередко для удобства подобные слагаемые подчеркивают, причем каждую группу подобных слагаемых подчеркивают разным типом подчеркиваний:
Теперь зная, что такое подобные слагаемые, приступим к их сложению (приведению).
Чтобы привести (сложить) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Пример:
Возьмем то же выражение и приведем в нем подобные слагаемые.
Как вы видите, процесс очень похож на вынесение общего множителя. В данном случае общим множителем для подобных слагаемых является их одинаковая буквенная часть.
Если мы видим в сумме слагаемое со знаком «минус» перед ним, то и коэффициенты мы будем складывать с этим же знаком.
Пример:
Приведем подобные слагаемые в выражении \(\mathbf<5c+4a-2c+3a>\)
Также достаточно часто встречаются задания вида «раскройте скобки и приведите подобные слагаемые».
Пример:
Раскроем скобки и приведем подобные слагаемые в выражении \(\mathbf<5a(c+3d)-4c(a-d)>\)
В целом, ничего нового в этом задании нет, надо просто аккуратно применить те приемы, которые мы уже освоили.
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Мы уже говорили про математику в литературе, но речь была про малоизвестные случаи.
Наш урок имеет порядковый номер 42, а это число является крайне популярным в культуре!
Известно оно стало из-за книги Дугласа Адамса «Автостопом по галактике».
В ней сверхразумная раса существ создала мощный компьютер с названием «Думатель» (Deep Thought) с одной лишь целью: найти «Окончательный Ответ на величайший вопрос Жизни, Вселенной и Всего Такого».
После семи с половиной миллионов лет работы компьютер выдал один ответ: число 42.
Дальше отрывок из книги, как отреагировали существа:
“— Сорок два! — взвизгнул Лунккуоол. — И это всё, что ты можешь сказать после семи с половиной миллионов лет работы?
— Я всё очень тщательно проверил, — сказал компьютер, — и со всей определённостью заявляю, что это и есть ответ. Мне кажется, если уж быть с вами абсолютно честным, то всё дело в том, что вы сами не знали, в чём вопрос.
— Но это же великий вопрос! Окончательный вопрос жизни, Вселенной и всего такого! — почти завыл Лунккуоол.
— Да, — сказал компьютер голосом страдальца, просвещающего круглого дурака. — И что же это за вопрос? “
Книга оказалась крайне популярной и читающее сообщество начало гадать, что могло означать это число, какой смысл вкладывал автор.
Но само число стало частью культуры, и, например, в сообществе программистов, часто можно встретить примеры с именно этим числом.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации