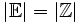Что такое равномощные множества
Равномощные множества



Определение. Множества Х и У называются равномощными, если между ними можно установить взаимно однозначное соответствие.
Если множества Х и У равномощны, то пишут Х
Нетрудно видеть, что множества рассмотренные в предыдущих примерах равномощны.
Равномощными могут быть как конечные, так и бесконечные множестваРавномощные конечные множества называют еще равночисленными. В начальном обучении математике равночисленность выражается словами «столько же» и может использоваться при ознакомлении учащихся со многими понятиями. Например, чтобы ввести равенство чисел, сравнивают два множества, устанавливая между их элементами взаимно однозначное соответствие. Например, пишут, что 5 = 5, так как кружков столько же, сколько квадратов.
 |
Как уже было сказано, равномощными могут быть и бесконечные множества.
Пусть Х – множество точек отрезка АВ, У – множество точек отрезка СD, причем длины отрезков различны. Так как между данными множествами можно установить взаимно однозначное соответствие, то множества точек АВ и СD равномощны.
Рассмотрим множество N натуральных чисел и множество У – четных натуральных чисел. Они равномощны, так как между их элементами можно установить взаимно однозначное соответствие:
 |
Замечание.На первый взгляд кажется парадоксальным тот факт, что можно установить взаимно однозначные соответствия между множеством и его частью: для конечных множеств такая ситуация невозможна. Однако в математике доказано, что для бесконечного множества А всегда найдется такое его подмножество В, что между А и В можно установить взаимно однозначноесоответствие. Иногда это утверждение считают определением бесконечного множества.
Определение.Если бесконечное множество равномощно множеству N натуральных чисел, его считают счетным.
Любое бесконечное подмножество множества N счетно: чтобы пронумеровать его элементы, надо расположить элементы подмножества в порядке возрастание и нумеровать один за другим. Так, счетно множество всех нечетных натуральных чисел, множество натуральных чисел, кратных 5 и др. Счетными являются также множества всех целых чисел, всех рациональных.
Существуют ли множества, отличные от счетных? Доказано, что бесконечным множеством, не равномощным множеству N натуральных чисел, является множество R всех действительных чисел.
О равномощности множеств
Парадокс Галилея – пример, иллюстрирующий свойства бесконечных множеств. В двух словах: натуральных чисел столько же, сколько квадратов натуральных чисел, то есть в множестве 1, 2, 3, 4, … столько же элементов, сколько в множестве 1, 4, 9, 16 …
В своей последней работе «Две Науки», Галилей привёл два противоречащих друг другу суждения о натуральных числах:
Суждение1. Некоторые числа являются точными квадратами (т.е. квадратами других целых чисел), другие же числа таким свойством не обладают.
Вывод1. Таким образом, точных квадратов должно быть меньше, чем всех чисел.
Суждение2. Для каждого натурального числа найдётся его точный квадрат, и наоборот – для каждого точного квадрата найдётся целый квадратный корень.
Вывод2. Точных квадратов и натуральных чисел должно быть одинаковое количество.
Галилей сделал вывод, что судить об одинаковом количестве элементов можно только для конечных множеств.
В 19 веке, Георг Кантор, используя свою теорию множеств показал, что можно ввести «количество элементов» для бесконечных множеств – так называемая мощность множества. При этом мощности множества натуральных чисел и множества точных квадратов совпали (оказалось верным второе суждение Галилея).
Применение термина «равномощность» к бесконечным множествам некорректно, т.к. бесконечные множества не могут быть равными по мощности, по крайней мере не существует однозначного метода это установить. Можно говорить определённо только про неравномощные множества (например, множество действительных чисел мощнее натуральных). Но рассматривая бесконечные множества равномощные натуральному множеству, приходится признать что это не равномощность, а неопределённость.
Т.е. в зависимости от порядка сопоставления элементов из разных множеств друг с другом, мы получаем разные результаты. Современная теория множеств считает, что это свидетельствует о том, что часть равна целому (часть множества Z также равномощна и N, и Z). На самом же деле мы не можем однозначно утверждать равномощны ли эти множества, это неопределённость.
Равномощность и мощность множеств



Операции над образами и прообразами отображений и их свойства
Поскольку образы и прообразы отображений являются множествами, то над ними определены все множественные операции: объединение, пересечение, абсолютное и относительное дополнение. Все ранее перечисленные свойства этих операций остаются в силе и для этого случая. Кроме того, имеют место следующие свойства:
Заметим, что если f – взаимно-однозначное отображение, то в пунктах 3, 5 и 8 имеет место равенство.
Два множества А и В называются равномощными или эквивалентными, если между их элементами можно установить взаимно-однозначное соответствие или если существует биекция А на В. Обозначение: А
В. Мощность – это то общее, что имеется у всех равномощных между собой множеств. Будем обозначать мощность множества А так: Р(А) или |A|.
Некоторые свойства равномощности:
1) Рефлексивность: А
А для любого множества А.
2) Симметричность: для любых множеств А и В, если А
3) Транзитивность: для любых множеств А, В и С, если А
Для доказательства каждого из этих свойств достаточно указать биекцию между множествами. Так в первом случае – это тождественное отображение А на А.
Утверждение: два конечных множества равномощны или эквивалентны тогда и только тогда, когда у них одинаковое число элементов.
Таким образом, мощность характеризует количество элементов множества. И для конечного множества, состоящего из n элементов, его мощность равна n. Для бесконечных множеств понятие «мощности» аналогично понятию «числа элементов», говорят, что бесконечные множества имеют бесконечную мощность. Итак, каждому множеству можно сопоставить некоторый объект – «мощность», называемый также «кардинальным числом», причем |A| = |В| Û А
2) Функция f(x)=10x устанавливает равномощность отрезков [0;1] и [0;10].
3) Два любых отрезка [a,b] и [c,d], а также два любых интервала (a,b) и (c,d) равномощны. Действительно, запишем уравнение прямой, проходящей через точки (а,с) и (b,d): 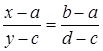
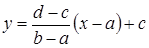
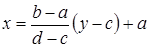
5) Любое конечное множество, состоящее из k элементов, равномощно отрезку натурального ряда <1,2,3,¼,k>. Поэтому элементы конечного множества могут быть перенумерованы: а1,а2,¼,аk.
Теорема 1.11.1. Конечное множество не равномощно никакому собственному подмножеству и никакому собственному надмножеству.
Теорема 1.11.2. Число элементов конечного множества всегда больше числа элементов любого его собственного подмножества. Или мощность конечного множества всегда больше мощности любого его собственного подмножества.
Теорема 1.11.3. Любое подмножество конечного множества само конечно. Любое надмножество бесконечного множества само бесконечно.
Из последней теоремы следует, что отрезок [0,1] – бесконечное множество, т.к. является надмножеством бесконечного множества чисел вида 1/n, где n – натуральное.
Бесконечное множество, равномощное множеству всех натуральных чисел называется бесконечно–счетным. Т.е. счетность множества есть не что иное, как возможность перенумеровать все элементы множества при помощи натуральных чисел так, чтобы все числа были использованы и различным элементам соответствовали различные числа. Конечные множества и счетно–бесконечные называются просто счетными.
Свойства счетных множеств.
1) Любое подмножество счетного множества само счетно.
2) Объединение конечного числа счетных множеств – счетное множество.
3) Объединение счетного числа конечных множеств – счетное множество.
4) Объединение счетного числа счетных множеств – счетное множество.
Действительно, обозначим множества М1, М2,¼, а элементы i–го множества: mi1,mi2,¼. Существует лишь конечное число элементов mik, для которых i+k=2, аналогично существует лишь конечное число элементов mik: i+k=3 и т.д.. Перенумеруем сначала все элементы, для которых i+k=2 (например, по возрастающим значениям i), затем (с помощью последующих чисел) все элементы, для которых i+k=3 и т.д.. При этом каждый элемент mik получит номер и различные mik будут иметь различные номера.
5) Если А и В – счетные множества, то А ´ В – счетное. Действительно, т.к. А´В=<(аi,bj): aiÎA, bjÎB>, то для нумерации таких пар можно воспользоваться той же идеей, т.е. перенумеровать сначала пары, для которых i+j=2, затем с помощью следующих натуральных чисел пары, для которых i+j=3 и т.д..
6) Множество рациональных чисел счетно. Действительно, т.к. ℚ=<x: x=a/b, где aÎℤ и bÎℕ>, то «хÎℚÞ х является корнем уравнения bx–a=0. Рассмотрим h=b+|a|, перенумеруем сначала все рациональные корни, для которых h=1, затем новые корни, получающиеся при h=2 и т.д..
7) Множество полиномов с рациональными коэффициентами счетно. Сопоставим каждому полиному последовательность (а1, а2, ¼,аn), составленную из его коэффициентов. Далее поступим аналогично тому, как это было сделано в пункте 6.
8) Множество всех алгебраических чисел (корней полиномов с рациональными коэффициентами) счетно.
Множество называется множеством мощности континуум, если оно равномощно множеству точек отрезка [0,1].
Теорема 1.11.4. (Кантора) Множество точек отрезка [0,1] несчетно.
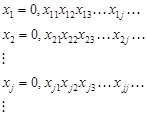
Из этой теоремы следует, что всякий отрезок [a,b] числовой прямой имеет мощность континуум, поскольку [a,b]
[0,1], т.к. f(x)=a+(b–a)x, где хÎ[0,1] – биекция. Кроме того, всякий интервал (a,b) имеет мощность континуум, поскольку (a,b)
[0,1]; в последнем случае закон биективного отображения может быть, например, таким:
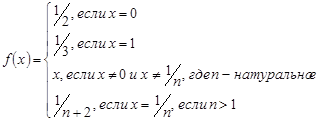
Отсюда также следует, что множество всех вещественных чисел имеет мощность континуум. А также множество всех иррациональных чисел (и иррациональных чисел, содержащихся в любом интервале числовой прямой) несчетно, т.к. оно получается из несчетного множества удалением из него счетного подмножества. Поэтому между любыми двумя вещественными числами найдется иррациональное число и даже несчетно много их.
Из всех бесконечных множеств счетные множества являются «наименьшими».
Теорема 1.11.5. Всякое бесконечное множество содержит счетное подмножество.
Доказательство: (по индукции) Пусть М – бесконечное множество. Тогда М¹Æ. Выберем какой-нибудь элемент из М и обозначим его а1. Пусть в М выбрано уже таким образом n различных элементов: а1, а2, ¼, аn. Так как M – бесконечно, то множество An=M \ <а1, а2, ¼, аn>¹Æ, и можно выбрать элемент из An и обозначить его аn+1. Ясно, что аn+1 отличается от всех ранее выбранных, и множество <а1, а2, ¼, аn>∪<аn+1> счетно и является подмножеством М.
Теорема 1.11.6. (О равномощности бесконечного множества собственному подмножеству) Всякое бесконечное множество равномощно своему некоторому собственному подмножеству.
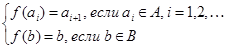 |
Доказательство: по предыдущей теореме множество М содержит счетное подмножество A=<а1,а2,¼,аn, ¼>. Пусть В=М \ А Ê Æ. Определим отображение f: M®M следующим образом:
Очевидно, что f является биективным отображением множества М на его собственное подмножество М \ <a1>, что и доказывает теорему.
Равномощность
Мощность множества или кардинальное число множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные.
Существуют бо́льшие, есть ме́ньшие бесконечные множества, среди них счётное множество является самым маленьким.
Содержание
Определение
Два множества называются равномощными, если между ними существует биекция. Существование биекции между множествами есть отношение эквивалентности, а мощность множества — это соответствующий ему класс эквивалентности.
Пример
Множество чётных целых чисел 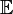

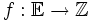
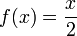
Свойства
Связанные определения
Следуя Кантору, мощность множества называется кардинальным числом, и обозначается мощность такого множества A через | A | (сам Кантор использовал обозначение 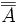
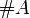
Мощность множества натуральных чисел 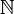
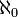
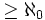
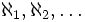
Для мощностей, как и в случае конечных множеств, имеются понятия: равенство, больше, меньше. То есть для любых множеств A и B возможно только одно из трёх:
Ситуация, в которой A и B не равномощны и ни в одном из них нет части, равномощной другому, невозможна. Это следует из теоремы Цермело. Иначе это означало бы существование несравнимых между собой мощностей (что в принципе возможно, если не принимать аксиому выбора).
Литература
Полезное
Смотреть что такое «Равномощность» в других словарях:
равномощность — сущ., кол во синонимов: 1 • равносильность (6) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
равномощность — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN equipotent … Справочник технического переводчика
ЭКВИВАЛЕНТНОСТЬ — (от позднелат. aequivalens равноценный, равнозначный), отношение типа равенства, общее назв. для рефлексивных, симметричных и транзитивных отношений, таких, напр., как равночис ленность, подобие, изоморфизм (см. Изоморфизм и гомоморфизм)… … Философская энциклопедия
Множеств теория — учение об общих свойствах множеств, преимущественно бесконечных. Понятие множества, или совокупности, принадлежит к числу простейших математических понятий; оно не определяется, но может быть пояснено при помощи примеров. Так, можно… … Большая советская энциклопедия
Эквивалентность — наименование отношений типа равенства, т. е. рефлексивных (см. Рефлексивность), симметричных (см. Симметричность) и транзитивных (см. Транзитивность) бинарных отношений (См. Отношение). Например: конгруэнтность или подобие геометрических… … Большая советская энциклопедия
КАНТОР — (Cantor) Георг (1845 1918) немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19 20 вв. Окончил Университет Берлина (1867), профессор… … История Философии: Энциклопедия
РАВЕНСТВО ( и ) — РАВЕНСТВО (в логике и математике) отношение между выражениями языка логики и математики, верное тогда (и только тогда), когда оба выражения обозначают один и тот же предмет, т.е., когда все, что можно сказать на языке данной теории про объект,… … Философская энциклопедия
МНОЖЕСТВО — набор, совокупность, собрание к. л. объектов, называемых его элементами, обладающих общим для всех них характеристич. свойством. Понятие M. принадлежит к числу первоначальных матем. понятий и может быть пояснено только при помощи примеров. Так,… … Физическая энциклопедия
РЕКУРСИВНОЙ ЭКВИВАЛЕНТНОСТИ ТИП — класс эквивалентности для отношения рекурсивной эквивалентности, т. е. совокупность всех подмножеств натурального ряда, каждые два из к рых могут быть приведены во взаимно однозначное соответствие с помощью частично рекурсивной функции. Таким… … Математическая энциклопедия
Равномощные множества. Способы установления равномощности множеств. Счетные и несчетные множества.
Определение. Множества X и Y называются равномощными, если между ними можно установить взаимно однозначное соответствие.
Если множества X и Y равномощны, то пишут X
Нетрудно увидеть, что множества, которые были рассмотрены в примерах 1 и 2, равномощны.
Равномощными могут быть как конечные, так и бесконечные множества. Равномощные конечные множества называют еще равночисленными. В начальном обучении математике равночисленность выражается словами «столько же» и может использоваться при ознакомлении учащихся со многими другими понятиями. Например, чтобы ввести равенство чисел, сравнивают два множества, устанавливая между их элементами взаимно однозначное соответствие. Например, пишут, что 5 = 5, так как кружков столько же, сколько квадратов (рис. 76).
Как уже было сказано, равномощными могут быть и бесконечные множества. Приведем примеры таких множеств.




На первый взгляд кажется парадоксальным тот факт, что можно установить взаимно однозначные соответствия между множеством и его частью: для конечных множеств такая ситуация невозможна. Однако в математике доказано, что для бесконечного множества А всегда найдется такое его подмножество B, что между А и В можно установить взаимно однозначное соответствие. Иногда это утверждение считают определением бесконечного множества.
Если бесконечное множество равномощно множеству N натуральных чисел, его называют счетным. Любое бесконечное подмножество множества N счетно: чтобы пронумеровать его элементы, надо расположить элементы подмножества в порядке возрастания и нумеровать один за другим (т.е. так, как это сделано в примере 4). Так, счетно множество всех нечетных натуральных чисел, множество натуральных чисел, кратных 5 и др. Счетными являются также множества всех целых чисел, всех рациональных.
Существуют ли множества, отличные от счетных? Доказано, что бесконечным множеством, не равномощным множеству N натуральных чисел, является множество R всех действительных чисел.
Упражнения
1.Задайте при помощи графа три соответствия между множествами X = и Y = <2, 4, 6>так, чтобы одно из них было взаимно однозначным.
3.Как можно изменить множества X и Y, данные в упражнении 2, чтобы соответствие Р: «прямоугольник х имеет площадь, равную у», было взаимно однозначным?
4.Даны множества: А = <1, 2, 5>, В = <3, 7>. Найдите А х В и В х А. Верно ли, что найденные множества равномощны?
5.Докажите, что множество А счетно, если:
6. Покажите, что, выполняя нижеприведенные задания, учащиеся начальных классов используют понятие равночисленности множеств:
 |
а) Нарисуй на другой фигуре (рис. 80) столько же точек, сколько на первой (точки не пересчитывать).
б) Нарисуй, не считая, столько же квадратов и столько же отрезков, сколько на рисунке 81 треугольников.
в) У Димы было 28 марок, а у Коли на 7 марок больше. Сколько марок было у Коли?
г) У Маши 9 игрушек, а у Риты на 2 меньше. Сколько игрушек у Риты?
д) Для детского сада купили 4 зеленых мяча, а красных в 3 раза больше, чем зеленых. Сколько красных мячей купили детям?
е) Для детского сада купили 15 красных мячей, а зеленых в 3 раза меньше. Сколько зеленых мячей купили детям?
43. Основные выводы § 8
Изучая материал этого параграфа, мы установили, что любое соответствие S между двумя множествами X и Y есть подмножество декартова произведения этих множеств, т.е. S с X х Y. Выяснили, что соответствия задают также, как и множества вообще. Познакомились с новыми понятиями:
— соответствие, обратное данному;
— взаимно однозначное соответствие;
Установили, что графики взаимно обратных соответствий между числовыми множествами симметричны относительно биссектрисы 1-го и 3-го координатных углов.
Лекция 18. Числовые функции
1. Определение числовой функции как частного случая соответствия.. Способы задания функции. Область определения и область значения функции.
2. График функции. Свойство монотонности функции
§ 9. ЧИСЛОВЫЕ ФУНКЦИИ
В начальном курсе математики понятие функции и все, что с ним связано, в явном виде не изучается, но идея функциональной зависимости буквально пронизывает его, а правильное понимание таких свойств реальных явлений, как взаимозависимость и изменяемость, является основой научного мировоззрения. Безусловно, все это требует от учителя начальных классов определенных знаний о функции и ее свойствах, и прежде всего таких, которые помогут ему осуществлять в начальной школе пропедевтику понятия функции.
44. Понятие функции. Способы задания функций
Выполним два задания для младших школьников.
1) Увеличь каждое нечетное однозначное число в 2 раза.
| Уменьшаемое |
| Вычитаемое |
| Разность |
С какими математическими понятиями мы имеем дело, выполняя эти задания?
Определение.Числовой функцией называется такое соответствие между числовым множеством X и множеством R действительных чисел, при котором каждому числу из множества X сопоставляется единственное число из множества R.
Множество X называют областью определения функции.
Функции принято обозначать буквами f, g, h и др. Если f— функция, заданная на множестве X, то действительное число у, соответствующее числу x из множества X, часто обозначают f(х) и пишут у = f(х). Переменную х при этом называют аргументом (или независимой переменной) функции f. Множество чисел вида f(х) для всех х из множества X называют областью значений функции f.
В рассмотренном выше первом примере функция задана на множестве X = <1, 3, 5, 7>— это ее область определения. А область значений этой функции есть множество <2, 6, 10, 14>.
Из определения функции вытекает, что для задания функции необходимо указать, во-первых, числовое множество X, т.е. область определения функции, и, во-вторых, правило, по которому каждому числу из множества X соответствует единственное действительное число.