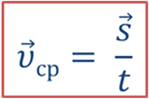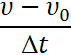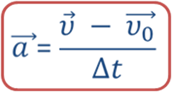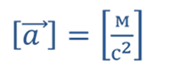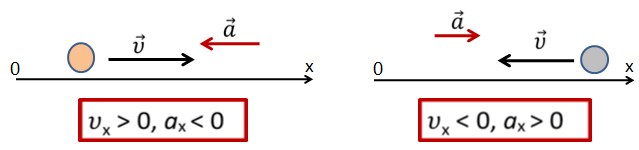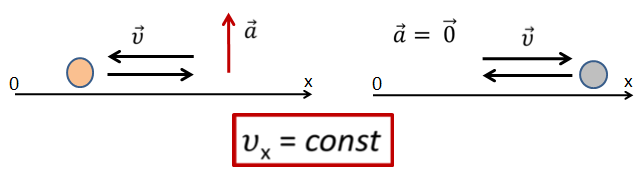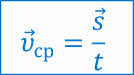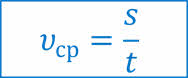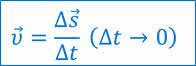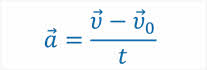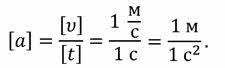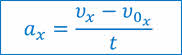Что такое равноускоренное движение 9 класс

Прямолинейное равноускоренное движение. Ускорение

Урок 3. Физика 9 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Прямолинейное равноускоренное движение. Ускорение»

Известно, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

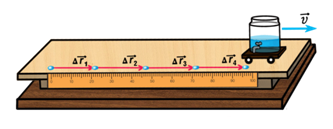
Ранее рассматривался простейший вид механического движения — равномерное прямолинейное движение. Равномерное движение — это движе­ние, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Однако, в повседневной жизни, люди сталкиваются с другим, более сложным видом движения. Трогается или тормозит автомобиль, взлетает или садится самолет. Во всех этих случаях скорость движения постоянно меняется. Такое движение в физике назвали неравномерным.

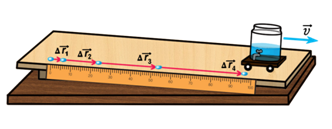
Неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения, или, говорят, меняется проекция вектора скорости.

Неравномерное движение бывает двух видов — ускоренным, это когда скорость тела увеличивается с течением времени, и замедленным, когда скорость тела уменьшается с течением времени.

При рассмотрении неравномерного движения пользоваться понятием скорости не целесообразно, так как скорость тела постоянно меняется с течением времени. Поэтому, в некоторых случаях, пользуются понятием средней скорости.

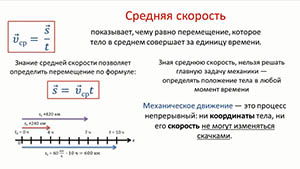
Средняя скорость показывает, чему равно перемещение, которое тело в среднем совершает за единицу вре­мени.

Если, например, троллейбус, двигаясь по прямой, проходит 600 км за 10 ч, то это значит, что в среднем он за каждый час прохо­дит 60 км.

Но ясно, что какую-то часть времени троллейбус вовсе не двигался, а стоял на остановке; трога­ясь с нее, троллейбус увеличивал свою скорость, приближаясь к ней — уменьшал ее. Все это не принимается во внимание и считается, что троллейбускаж­дый час проходитпо 60 км.

Знание средней скорости позволяет определить перемещение по формуле

При этом надо помнить, что эта формула дает верный ре­зультат только для того участка траектории, для которого опре­делена средняя скорость. Если, пользуясь значением средней скорости в 60 км/ч, вычислять перемещение троллейбуса не за 10 часов, а за 4 часа или 7 часов, то мы полу­чим неверный результат.

В данном случае была сделана попытка свести неравномерное движение к рав­номерному движению и для этого была введена средняя скорость движения. Но это нам не помогло: зная среднюю скорость, нельзя решать главную задачу механики — определять положение тела в любой момент времени. Можно ли каким-нибудь другим способом свести не­равномерное движение к равномер­ному?

Этого сделать нельзя, потому что механическое движение — это процесс непре­рывный: ни координаты тела, ни его скорость не могут изме­няться скачками.

Следовательно, в каждой точке траектории движения и в каждый момент времени ско­рость тела имеет определенное значение.

Скорость тела в данный момент времени или в данной точке траектории называют мгно­венной скоростью.

Мгновенная скорость — величина векторная. Она направлена по касательной к траектории в каждой её точке в сторону перемещения.

При неравномерном движении мгновенная скорость тела непрерывно изменяется: от точки к точке, от одного момента времени к другому. Как же вычислить мгновенную скорость тела?

Для вычисления перемещения тела в любой момент времени нужно было знать, как быстро оно изменяется с течением времени. Точно так же для вычисления скорости в любой момент времени нужно знать, как быстро она изменяется, или, говорят, каково изменение скорости в единицу времени.

Для простоты будем рассматривать такое прямолинейное неравномерное движение тела, при котором его ско­рость за любые равные про­межутки времени изменяется одинаково. Такое движение назы­вается равноускоренным.

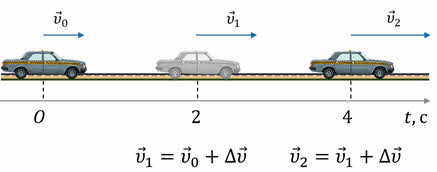
Если в некоторый начальный момент времени скорость тела равна υ₀, а через некоторый промежуток вре­мени она оказывается равной υ, то за каждую единицу времени скорость изменяется на величину

Эта величина и характеризует быстроту изменения скорости. Ее называют ускоре­нием и обозначают латинской буквой а:

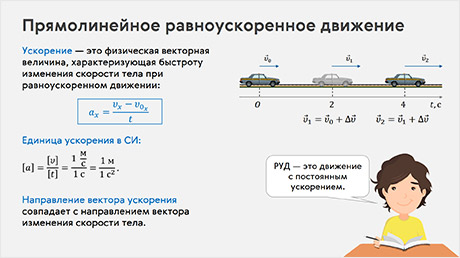
Ускорение — физическая векторная величина, характеризующая быстроту изменения скорости и численно равная отношению изменения скорости тела к промежутку времени, в течение которого это изменение про­изошло.

В системе СИ ускорение измеря­ется в

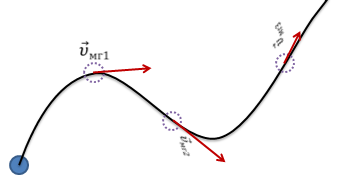
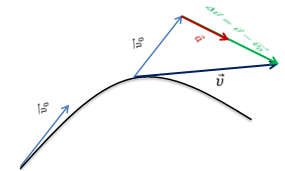
Определим направление вектора ускорения в некоторый момент времени. Для этого необходимо найти вектор изменения скорости тела. Что бы это сделать, необходимо начало вектора υ₀ параллельным переносом совместим с началом вектора υ. Достроим рисунок до треугольника. В результате получаем вектор разности двух векторов. Он направлен в сторону уменьшаемого вектора, в нашем случае, к вектору конечной скорости.

Направление вектора ускорения совпадает с направлением вектора изменения скорости тела.

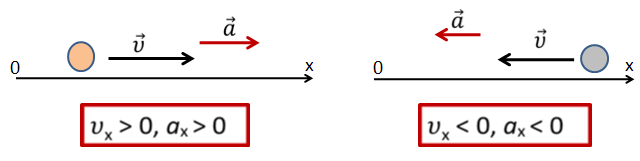
Рассмотрим связь знаков проекций скорости и ускорения с характером движения тела. Если вектор скорости сонаправлен с вектором ускорения (т.е. вектор скорости направлен в ту же сторону, что и вектор ускорения), то скорость тела увеличивается.

Если вектор скорости направлен в сторону, противоположную вектора ускорения, то скорость тела уменьшается.

И, наконец, скорость тела постоянна, если вектор ускорения равен нулю или перпендикулярен вектору скорости.

· Неравномерное движение — это такое движение, при котором тело, за любые равные промежутки времени совершает разные перемещения.

· В некоторых случаях, когда имеют дело с неравномерным дви­жением, пользуются понятием средней скорости, которая показывает, чему равно перемещение, которое тело в среднем совершает за единицу вре­мени.

· В каждой точке траектории движения и в каждый момент времени ско­рость тела имеет определенное значение.

· Скорость тела в данный момент времени или в данной точке траектории называют мгно­венной скоростью.

· Мгновенная скорость — величина векторная. Она направлена по касательной к траектории в каждой её точке в сторону перемещения.

· Основной характеристикой неравномерного движения является ускорение. Ускорение — физическая векторная величина, характеризующая быстроту изменения скорости и численно равная отношению изменения скорости тела к промежутку времени, в течение которого это изменение про­изошло.

· Ускорение измеря­ется в метрах на секунду в квадрате.

· Если векторы ускорения и скоростисонаправлены, то скорость тела увеличивается.

· Если векторы ускорения и скорости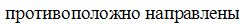, то скорость тела уменьшается.

· Скорость тела постоянна, если вектор ускорения равен нулюили перпендикулярен вектору скорости.

Источник

Прямолинейное равноускоренное движение. Ускорение

Урок 5. Физика 9 класс (ФГОС)

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Прямолинейное равноускоренное движение. Ускорение»

Вы знаете, равномерное прямолинейное движение — это модель реального движения тел. Автомобили, корабли, самолёты и другие тела чаще всего движутся и не прямолинейно, и не равномерно. Как же описать такое движение, ведь уравнением движения мы пользоваться не можем, так как скорость тела постоянно меняется?

Для описания быстроты изменения положения тела с течением времени при неравномерном движении, вводится понятие средней скорости. Она показывает, какое перемещение в среднем совершало тело за единицу времени.

Но пользоваться этой формулой для определения модуля средней скорости можно лишь в том случае, если тело движется вдоль прямой в одну сторону. Во всех остальных случаях эта формула не работает.

Поэтому на практике пользуются понятием средней путевой скорости, с которым вы знакомы ещё с седьмого класса. Напомним, что средняя путевая скорость определяется отношением пути к промежутку времени, за который этот путь пройден. Она показывает, какой путь в среднем проходило тело за единицу времени.

Однако следует помнить, что средняя скорость характеризует движение за весь промежуток времени в целом. Она не даёт информации о скорости движения в каждой точке траектории (или в каждый момент времени). Например, если мотоциклист преодолел путь в 300 километров за 6 часов, то средняя скорость его движения равна 50 км/ч. Иными словами, в среднем мотоциклист за каждый час проезжал 50 километров. Однако при этом он мог какое-то время стоять, какое-то время двигаться с большей или меньшей скоростью. Значит, зная среднюю скорость мотоциклиста за 6 часов, мы не сможем определить его положение через час или два.

Поэтому для описания такого движения вводится понятие мгновенной скорости, то есть скорости движения в данный момент времени или в данной точке траектории.

— А как определить мгновенную скорость тела?

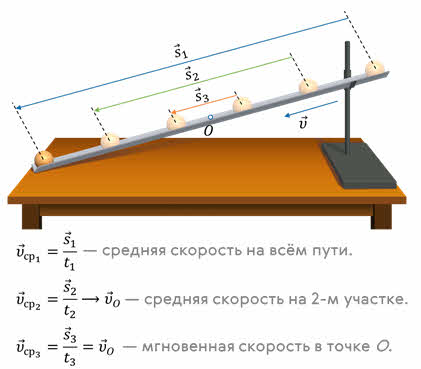
Рассмотрим пример. Пусть шарик скатывается по наклонному жёлобу. Нас интересует мгновенная скорость шарика, например, в точке О его траектории. Выделим небольшой участок траектории, включающий в себя точку О. Разделив перемещение шарика на этом участке траектории, на соответствующий промежуток времени найдём среднюю скорость перемещения на этом участке. Это именно средняя скорость, потому что скорость непрерывно изменяется, и в разных местах участка она разная. Рассмотрим меньшее перемещение — участок два. Оно произойдёт за меньший промежуток времени. Средняя скорость шарика на этом участке хотя и не равна скорости в точке О, но уже ближе к ней.

При дальнейшем уменьшении перемещений и промежутков времени мы будем получать средние скорости, которые все меньше отличаются друг от друга и от мгновенной скорости шарика в точке О. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время (движение станет как бы равномерным). Средняя скорость на этом участке и будет являться мгновенной скоростью шарика в точке О.

Таким образом, мгновенная скорость — это векторная физическая величина, равная отношению достаточно малого перемещения к малому промежутку времени, в течение которого это перемещение совершается:

Как следует из формулы, направление мгновенной скорости совпадает с направлением движения тела. В дальнейшем мгновенную скорость мы будем называть просто скоростью.

Из всех видов неравномерного движения мы будем изучать самое простое — прямолинейное равноускоренное движение. Прямолинейным равноускоренным движением называется такое движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и туже величину, а траекторией движения тела является прямая линия.

В физике существует величина, характеризующая быстроту изменения скорости тела при равноускоренном движении. Она называется ускорением и обозначается малой латинской буквой а.

Для того, чтобы найти ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло. Таким образом, равноускоренное движение — это движение с постоянным ускорением.

За единицу ускорения в СИ принимается ускорение такого прямолинейного равноускоренного движения, при котором за 1 секунду скорость тела изменяется на 1 м/с:

Ускорение — это векторная величина, направление которой, как следует из формулы, совпадает с направлением вектора изменения скорости тела.

Например, при разбеге самолёта направление вектора ускорения и векторов скорости совпадают и самолёт движется ускоренно. При посадке, наоборот, самолёт замедляет своё движение. В этом случае вектор ускорение и векторы скорости имеют противоположные направления. Поэтому самолёт движется замедленно.

Конечно же, как и в случае со скоростью, при решении большинства задач, мы будем пользоваться формулой, в которую входит не сам вектор ускорения, а его проекция на координатную ось.

Определите среднюю скорость движения катера на участке прямолинейного пути, если первую его половину он прошёл со скоростью 12 м/с, а вторую — со скоростью 18 м/с.

Источник

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид :

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник