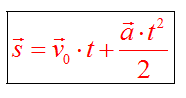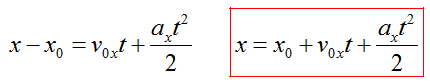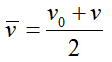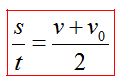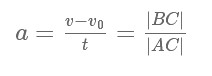Что такое равноускоренное движение

I. Механика

Тестирование онлайн

Равноускоренное движение

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.

Ускорение тела

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:

Направление вектора ускорения

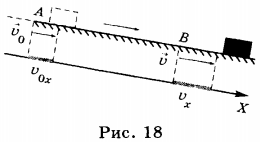
Направление вектора ускорения изображено на рисунках

На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.

При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.

На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.

При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.

Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.

При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус».

Перемещение при равноускоренном движении

Дополнительная формула, которую называют безвременной

Формула в координатах

Связь со средней скоростью

При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости

Из этого правила следует формула, которую очень удобно использовать при решении многих задач

Соотношение путей

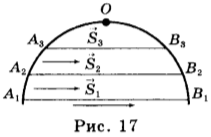
Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.

Главное запомнить

Упражнения

Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?

Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.

Какие из приведенных зависимостей описывают равноускоренное движение?

Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?

*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?

В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.

Источник

Равноускоренное движение: формулы и примеры

Содержание:

Определение

Равноускоренным движением в физике считается такое движение, вектор ускорения которого не меняется по модулю и направлению. Говоря простым языком, равноускоренное движение представляет собой неравномерное движение (то есть идущее с разной скоростью), ускорение которого является постоянным на протяжении определенного промежутка времени. Представим себе автомобиль, который начинает двигаться, первые 2 секунды его скорость равна 10 м/с, следующие 2 секунды он уже движется со скоростью 20 м/с, а еще через 2 секунды уже со скоростью 30 м/с. То есть каждые 2 секунды он ускоряется на 10 м/с, такое движение и есть равноускоренным.

Отсюда можно вывести предельно простое определение равноускоренного движения: это такое движение любого физического тела, при котором его скорость за равные промежутки времени изменяется одинаково.

Примеры

Наглядным примером равноускоренного движения в повседневной жизни может быть велосипед, едущий с горки вниз (но не велосипед, управляемый велосипедистом), или брошенный камень под определенным углом к горизонту.

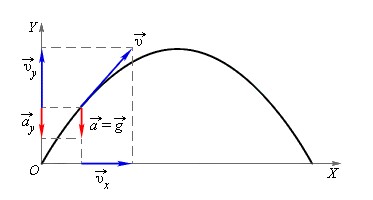
К слову пример с камнем можно рассмотреть более детально. В любой точке траектории полета на камень действует ускорение свободного падения g. Ускорение g не меняется, то есть остается константой и всегда направлено в одну сторону (по сути, это главное условие равноускоренного движения).

Полет брошенного камня удобно представить в виде сумы движений относительно вертикальной и горизонтальной оси системы координат.

Если вдоль оси Х движение камня будет равномерным и прямолинейным, то вдоль оси Y равноускоренным и прямолинейным.

Формула

Формула скорости при равноускоренном движении будет иметь такой вид:

Где V₀ – это начальная скорость тела, а – ускорение (как мы помним, эта величина является константой), t – общее время полета камня.

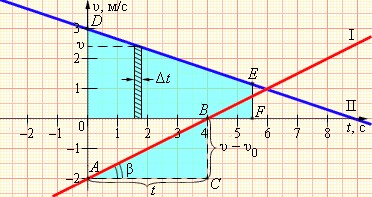
При равноускоренном движении зависимость V(t) будет иметь вид прямой линии.

Ускорение может быть определено по углу наклона графика скорости. На этом рисунке оно равно отношению сторон треугольника АВС.

Чем больше угол β, тем больше наклон и как следствие, крутизна графика по отношению к оси времени, и тем больше будет ускорение тела.

Рекомендуемая литература по теме

Видео

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.

Похожие посты:

Один комментарий

Источник

Уравнения равноускоренного движения

При постоянном ускорении скорость физического тела равномерно возрастает, начиная с нуля.

Расстояние, пройденное равноускоренным телом, начиная с нулевой скорости, пропорционально квадрату времени.

Галилео Галилей относится к числу людей, прославившихся совсем не тем, за что им следовало бы пользоваться заслуженной славой. Все помнят, как этого итальянского естествоиспытателя в конце жизни подвергли суду инквизиции по подозрению в ереси и заставили отречься от убеждения, что Земля вращается вокруг Солнца. На самом же деле, этот судебный процесс на развитие науки практически не повлиял — в отличие от ранее проделанных Галилеем опытов и сделанных им на основании этих опытов выводов, которые фактически предопределили дальнейшее развитие механики как раздела физической науки.

Движение физических тел изучалось с незапамятных времен, и основы кинематики были заложены задолго до рождения Галилея. Элементарные задачи описания движения сегодня изучают уже в начальной школе. Например, все знают, что если автомобиль равномерно движется со скоростью 20 км/ч, то за 1 час он проедет 20 км, за 2 часа — 40 км, за 3 часа — 60 км и т. д. И до тех пор, пока машина движется с постоянной скоростью (стрелка спидометра не отклоняется от заданного деления на его шкале), рассчитать пройденное расстояние труда не составляет — достаточно умножить скорость машины на время, которое она находится в пути. Этот факт известен настолько давно, что имя его первооткрывателя наглухо затерялось в тумане античных времен.

Сложности возникают, как только объект начинает двигаться с переменной скоростью. Трогаетесь вы, к примеру, от светофора — и стрелка спидометра ползет от нуля вверх, пока вы не отпустите педаль газа и не нажмете педаль тормоза. На самом деле стрелка спидометра на месте практически не стоит — она всё время движется вверх или вниз. В начале каждой отдельно взятой секунды реальная скорость машины одна, а в конце секунды — уже другая, и пройденный ею за секунду путь точно рассчитать не так-то просто. Эта проблема — описание движения с ускорением — волновала естествоиспытателей задолго до Галилея.

Сам же Галилео Галилей подошел к ней новаторски и, фактически, задал направление всего дальнейшего развития современной методологии естествознания. Вместо того чтобы сидеть и умозрительно решать вопрос о движении ускоряющихся тел, он придумал гениальные по своей простоте опыты, позволяющие экспериментально проследить, что в действительности происходит с ускоряющимися телами. Нам может показаться, что ничего особенно новаторского в таком подходе нет, однако до Галилея основным методом решения проблем «натурфилософии» — о чем говорит само название тогдашней естественной науки — было умозрительное осмысление происходящего, а не его экспериментальная проверка. Сама идея проведения физических экспериментов была в то время по-настоящему радикальной. Чтобы понять идею опытов Галилея, представьте себе тело, падающее под воздействием силы земного притяжения. Выпустите какой-нибудь предмет из рук — и он упадет на пол; при этом в первое мгновение скорость его движения будет равна нулю, но он тут же начнет ускоряться — и будет продолжать ускоряться, пока не упадет на землю. Если мы сможем описать падение предмета на землю, мы затем сможем распространить это описание и на общий случай равноускоренного движения.

Сегодня измерить динамику падения предмета не сложно — можно с большой точностью зафиксировать время от начала падения до любой промежуточной точки. Однако во времена Галилея точных секундомеров не было, да и любые механические часы по современным стандартам были весьма примитивны и неточны. Поэтому ученый первым делом разработал экспериментальный аппарат, позволяющий обойти эту проблему. Во-первых, он «разбавил» силу тяжести, замедлив время падения до разумных, с точки зрения имеющихся инструментов измерения, пределов, а именно — заставил тела скатываться по наклонной плоскости, а не просто падать отвесно. Затем он придумал, как обойти неточность современных ему механических часов, натянув на пути скатывающегося по наклонной поверхности шара ряд струн, чтобы он задевал их по дороге и можно было хронометрировать его движение по извлекаемым звукам. Раз за разом спуская шар по наклонной под рядом струн, Галилей перемещал струны, пока не добился, чтобы шар на всем своем пути, задевая натянутые струны, извлекал звуки через равные промежутки времени.

В конце концов Галилею удалось накопить достаточный объем экспериментальной информации о равноускоренном движении. Тело, стартующее из состояния покоя, далее движется так, как это описано в самом начале данной статьи. В переводе на язык математических символов равноускоренное движение описывается следующими уравнениями:

где a — ускорение, v — скорость, d — расстояние, пройденное телом за время t. Чтобы прочувствовать смысл этих уравнений, достаточно пристально пронаблюдать за падением предметов. Скорость падения зримо возрастает со временем, прошедшим с начала падения. Это следует из первого уравнения. Очевидно и то, что в процессе падения на прохождение первой части пути у тела уходит больше времени, чем на оставшуюся часть пути. Именно это и описывает вторая формула, поскольку из неё следует, что чем дольше тело ускоряется, тем больший отрезок пути оно преодолевает за одно и то же время.

Галилей сделал и еще одно важное наблюдение о теле, находящемся в состоянии свободного падения под воздействием силы гравитационного притяжения, хотя и не смог подтвердить его непосредственными измерениями. Экстраполировав результаты, полученные им при наблюдении скатывающихся по наклонной плоскости предметов, он сумел определить ускорение свободного падения тела на поверхность Земли. Ускорение свободного падения принято обозначать g, и оно равняется (приблизительно):

g = 9,8 м/с 2 (метра в секунду за секунду)

То есть, если уронить предмет из состояния покоя, за каждую секунду падения его скорость будет возрастать на 9,8 метра в секунду. На исходе первой секунды падения тело будет двигаться со скоростью 9,8 м/с, на исходе второй — со скоростью 2 × 9,8 = 18,6 м/с и так далее. Величина g определяет коэффициент ускорения падения тела, находящегося в непосредственной близости от земной поверхности, в связи с чем g принято называть ускорением свободного падения, или гравитационным ускорением.

Здесь следует сделать два важных замечания относительно полученных Галилеем результатов. Во-первых, ученый получил чисто экспериментальное значение величины g, ни на каких теоретических прогнозах не основывающееся. Значительно позже Исаак Ньютон в своих знаменитых работах показал, что величину g можно рассчитать теоретически, исходя из сочетания сформулированных им законов механики Ньютона и закона всемирного тяготения Ньютона. Именно первопроходческий труд Галилея и проложил дорогу последующим триумфальным открытиям Ньютона и формированию классической механики в её общеизвестном виде.

Второй важнейший момент состоит в том, что ускорение свободного падения не зависит от массы падающего тела. По сути, сила притяжения пропорциональна массе тела, но это полностью компенсируется большей инерцией, присущей более массивному телу (его нежеланию двигаться, если хотите), а посему (если не учитывать сопротивление воздуха) все тела падают с одинаковым ускорением. Это практическое заключение вступало в полное противоречие с умозрительными предсказаниями древних и средневековых натурфилософов, которые были уверены, что всякой вещи свойственно стремиться к центру мироздания (коим им, естественно, представлялся центр Земли) и что чем массивнее предмет, тем с большей скоростью он к этому центру устремляется.

Свое видение Галилей, конечно же, подкрепил экспериментальными данными, но вот опыта, который ему традиционно приписывают, он, скорее всего, вовсе не проводил. Согласно околонаучному фольклору, он сбрасывал предметы различной массы с «падающей» Пизанской башни, чтобы продемонстрировать, что они достигают поверхности земли одновременно. В этом случае, однако, Галилея ждало бы разочарование, поскольку более тяжелые предметы неизбежно падали бы на землю раньше легких из-за разницы в удельном сопротивлении воздуха. Если бы сбрасываемые с башни предметы были одного размера, сила сопротивления воздуха, тормозящая их падение, была бы одинаковой для всех предметов. При этом из законов Ньютона следует, что более легкие предметы затормаживались бы воздухом интенсивнее тяжелых и падали на землю позднее тяжелых предметов. А это, естественно, противоречило бы предсказанию Галилея.

Источник

Скорость. Ускорение. Равноускоренное прямолинейное движение

1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.

При неравномерном движении координату тола уже нельзя определить но формуле ​ \( x=x_0+v_xt \) ​, так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.

Средней скоростью ​ \( \vec_ <ср>\) ​ неравномерного движения называют физическую величину, равную отношению перемещении \( \vec \) тела ко времени ​ \( t \) ​, за которое оно произошло: ​ \( \vec_<ср>=\frac\) ​.

2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.

3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.

Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.

При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.

4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.

Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.

5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.

Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.

Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.

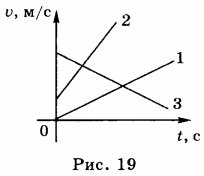
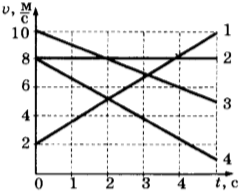
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.

График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_ <02>\) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_ <03>\) и с ускорением, направленным в сторону, противоположную направлению скорости.

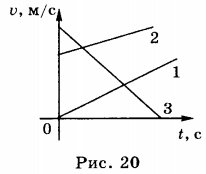
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).

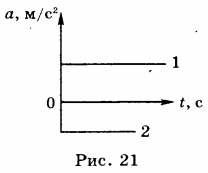
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.

График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.

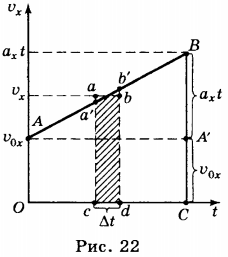
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).

Выделим на графике малый участок ​ \( ab \) ​ и опустим перпендикуляры из точек​ \( a \) ​ и ​ \( b \) ​ на ось абсцисс. Если промежуток времени ​ \( \Delta\) ​, соответствующий участку ​ \( cd \) ​ на оси абсцисс мал, то можно считать, что скорость в течение этого промежутка времени не изменяется и тело движется равномерно. В этом случае фигура ​ \( cabd \) ​ мало отличается от прямоугольника и её площадь численно равна проекции перемещения тела за время, соответствующее отрезку ​ \( cd \) ​.

На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время ​ \( t \) ​ численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: ​ \( S_x= \frac<1><2>(OA+BC)OC \) ​.

Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.

Если начальная скорость тела равна нулю, то: ​ \( v^2_x=2a_xs_x \) ​.

Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

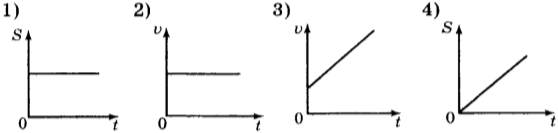
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?

2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?

1) 200 м/с 2
2) 20 м/с 2
3) 2 м/с 2
4) 0,5 м/с 2

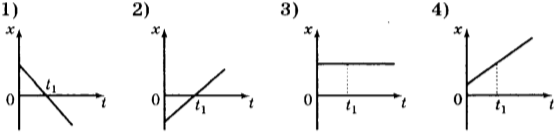
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси ​ \( Оx \) ​. У какого из тел в момент времени ​ \( t_1 \) ​ скорость движения равна нулю?

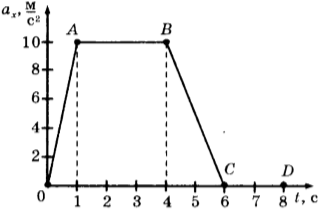
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси ​ \( Оx \) ​.

Равноускоренному движению соответствует участок

1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD

5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.

Чему равен путь, пройденный телом за третью секунду?

1) 4 м
2) 4,5 м
3) 5 м
4) 9 м

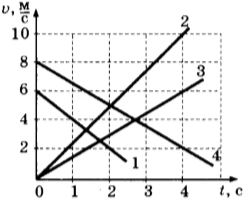
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.

Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?

1) только 1
2) только 2
3) только 4
4) 3 и 4

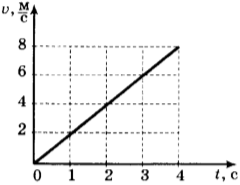
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.

8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?

1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с

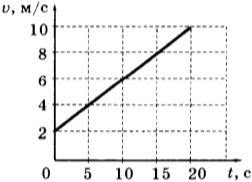
10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.

1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с

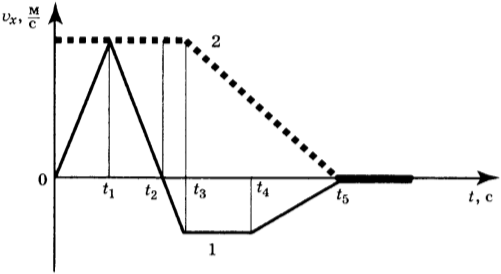
11. Два тела движутся по оси ​ \( Оx \) ​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​ \( t_3-t_5 \) ​ тело 2 движется равноускоренно.
2) К моменту времени ​ \( t_2 \) ​ от начала движения тела прошли одинаковые пути.
3) В промежутке времени ​ \( 0-t_3 \) ​ тело 2 находится в покое.
4) В момент времени ​ \( t_5 \) ​ тело 1 останавливается.
5) В промежутке времени ​ \( t_3-t_4 \) ​ ускорение ​ \( a_x \) ​ тела 1 отрицательно.

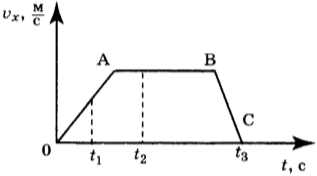
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени ​ \( t_1 \) ​ тело имело максимальное по модулю ускорение.
4) Момент времени ​ \( t_3 \) ​ соответствует остановке тела.
5) В момент времени ​ \( t_2 \) ​ тело имело максимальное по модулю ускорение.

Часть 2

13. Зависимость координаты от времени для некоторого тела описывается уравнением ​ \( x=12t-t^2 \) ​. В какой момент времени скорость движения равна нулю?

Источник