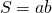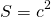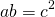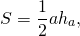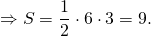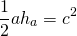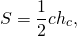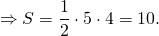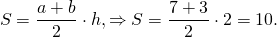Что такое равновеликий куб

Если каждое ребро куба увеличить

В одной из задач используется понятие равновеликости. Что это означает? Равновеликие тела это тела имеющие равный объём. Например, если сказано, что шар равновелик кубу – это означает, что шар и куб имеют равный объём. Рассмотрим задачи:

Если каждое ребро куба увеличить на 9, то его площадь поверхности увеличится на 594. Найдите ребро куба.

Так как существует зависимость площади поверхности куба от его ребра, то, конечно же, воспользуемся формулой площади поверхности куба:

Сказано, что при увеличении ребра на 9 площадь поверхности увеличивается на 594. Запишем формулу площади поверхности для увеличенного куба:

Ребро куба равно 1.

Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 16, 27. Найдите ребро равновеликого ему куба.

Равновеликий куб – это куб, объём которого равен объёму параллелепипеда. Известно, что объём куба находится по формуле:

Значит если мы найдём объём параллелепипеда, то сможем найти ребро куба. Объём параллелепипеда равен:

Во сколько раз увеличится объем куба, если его ребра увеличить в шесть раз?

Разделим V₂ на V₁ и получим искомую величину:

Объём куба увеличится в 216 раз.

Если каждое ребро куба увеличить на 3, то его объем увеличится на 819. Найдите ребро куба.

Пусть ребро куба равно a.

Запишем чему равен объём для исходного куба и для увеличенного:

Сказано, что объём увеличился на 819, значит:

Подходящее значение a = 8. Отрицательное значение для данной задачи не имеет физического смысла. Таким образом, ребро куба равно 8.

Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 24 раза?

Запишем формулу площади поверхности исходного куба и формулу площади поверхности для куба с увеличенным ребром:

Теперь остаётся только лишь найти отношение площадей:

Таким образом, площадь поверхности увеличится в 576 раз.

Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Отметим, что первый куб это больший куб, второй это меньший куб. Мы без труда решим эту задачу, если определим во сколько раз ребро первого куба больше ребра второго. Пусть ребро малого (второго) куба равно х, а большего у. Тогда

Получили, что ребро первого куба большего ребра второго в 9 раз, то есть

Теперь запишем площадь поверхности для обоих кубов:

Остаётся найти отношение площадей поверхностей кубов:

Площадь поверхности первого куба больше площади поверхности второго куба в 81 раз.

27061. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

27080. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.

27081. Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?

27102. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.

27168. Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Есть ещё отличный подход для решения задач, в которых где речь идёт о изменении объёма и площади поверхности для таких тел как: куб, параллелепипед, шар, правильная четырёхугольная пирамида, конус, цилиндр, при увеличении (уменьшении) ребра (радиуса) в некоторое количество раз. Такие задания практически можно решать в одну строчку. Об этом расскажу в будущем, не пропустите!

Источник

Стереометрия. Страница 7

Главная > Учебные материалы > Математика: Стереометрия. Страница 7

1.Объем. Объем прямоугольного параллелепипеда. 2.Наклонный параллелепипед. 3.Объем пирамиды. 4.Объем призмы. 5.Равновеликие тела. 6.Объемы подобных тел. 7.Примеры.

1. Объем

Объем прямоугольного параллелепипеда

Возьмем куб объемом одна единица и три прямоугольных параллелепипеда с измерениями: a:1:1, a:b:1, a:b:c (Рис.1.1). Обозначим их объемы как V₁, V₂, V. Тогда можно составить следующие соотношения:

Перемножив эти три равенства почленно, получим, что объем прямоугольного параллелепипеда равен: V = abc.

Рис. 1 Объем прямоугольного параллелепипеда.

Рис. 1.1 Объем прямоугольного параллелепипеда V = abc.

2.Наклонный параллелепипед

Пусть дан наклонный параллелепипед ABCDA’B’C’D’ (Рис.2). Проведем плоскость через ребро D’C’, перпендикулярную основанию ABCD и построим треугольную призму, у которой грань DD’C’С будет являтся общей с гранью параллелепипеда DD’C’С.

Отсечем точно такую же призму с другой стороны параллелепипеда AA’EBB’F. Отсюда следует, что объем параллелепипеда EFHOA’B’C’D’ равен объему исходного параллелепипеда ABCDA’B’C’D’. Так как мы добавили и отсекли треугольную призму одного и того же размера.

Объем параллелепипеда EFHOA’B’C’D’ равен произведению площади основания EFHO на высоту EA’.

Следует отметить, что если у параллелепипеда две соседние боковые грани находятся под некоторым углом к основанию, т.е. ≠ 90°, то такое преобразование необходимо проделать два раза.

Таким образом, в конечном итоге, можно получить прямоугольный параллелепипед, у которого все боковые грани находятся под прямым углом к основанию. Такое преобразование сохраняет объем параллелепипеда, площадь основания и высоту.

Следовательно, объем любого параллелепипеда равен произведению площади основания на высоту.

Рис.2 Наклонный параллелепипед

3.Объем призмы

Пусть дана треугольная призма ABCA’B’C’ (Рис.3). Достроим данную призму до параллелепипеда. Тогда точка пересечения диагоналей (точка О) параллелограмма BB’C’C будет являться точкой симметрии. Следовательно объем призмы будет равен половине объема параллелепипеда.

Так как объем параллелепипеда равен произведению площади основания на высоту, то объем призмы будет равен также произведению площади основания на высоту.

Допустим, что основание призмы есть многоугольник. Тогда его можно разбить на несколько треугольников. Следовательно вся призма будет представлять собой несколько треугольных призм. А общий объем будет равен сумме объемов этих призм.

Таким образом: объем любой призмы равен произведению площади ее основания на высоту.

Рис. 3 Объем призмы.

4. Объем пирамиды

Пусть дана треугольная пирамида ABCS c вершиной S и основанием ABC (Рис.4). Достроим эту пирамиду до треугольной призмы с той же высотой и тем же основанием ABC. Таким образом, треугольная призма будет состоять из трех одинаковых пирамид.
Пирамида ABCS с вершиной S.
Пирамида AECS с вершиной S.
Пирамида CEFS с вершиной S.

Пирамиды AECS и CEFS имеют равные основания AEC и CEF и общую вершину S и соответственно высоту. Следовательно, они имеют равные объемы.

Пирамиды ABCS и CEFS имеют также равные основания ABC и SFE и равные высоты, т.к. основания лежат в параллельных плоскостях.

Отсюда можно сделать вывод, что все три пирамиды имеют один и тот же объем. Таким образом, объем одной пирамиды равен одной трети объема призмы.

Если основание пирамиды представляет собой многоугольник, то его можно разбить на треугольники и объем такой пирамиды можно рассчитать как сумму объемов всех составляющих пирамид, т.к. они все имеют одну и ту же высоту.

Отсюда можно сделать вывод, что объем любой пирамиды равен одной трети произведения площади ее основания на высоту.

Объем усеченной пирамиды

Пусть дана усеченная пирамида ABCA’B’C’ (Рис.4.1). Достроим нашу пирамиду до полной с вершиной O. Тогда объем усеченной пирамиды будет равен разности двух пирамид.

Рис. 4 Объем пирамиды.

Рис. 4.1 Объем усеченной пирамиды.

5. Равновеликие тела

Два геометрических тела называются равновеликими, если они имеют равные объемы.

Тогда суммы объемов G_a и G_b можно рассчитать по формулам:

Если n будет стремиться к бесконечности, то дробь SH/n будет стремиться к нулю. Следовательно:

Отсюда можно сделать вывод, что две треугольные пирамиды с равными площадями оснований и равными высотами равновелики.

Рис. 5 Равновеликие тела.

6. Объемы подобных тел

Пусть даны два подобных куба Q₁ и Q₂ (Рис.6), которые имеют измерения Q₁:a,b,c и Q₂:ka,kb,kc c коэффициентом подобия k соответственно.

Тогда объем куба Q₁ равен V₁ = abc,
а объем куба Q₂ равен V₂ = ka kb kc = k 3 abc = k 3 V₁.

Следовательно, отношение объемов двух кубов равно k 3

Объем подобной фигуры:

Точно так же можно разбить тело на несколько пирамид. Тогда объем всего тела будет равен сумме всех составляющих его пирамид.

Отсюда можно сделать следующий вывод, что отношение объемов двух подобных тел равно кубу их коэффициента подобия.

Рис. 6 Объемы подобных тел.

7. Пример 1

Три латунных куба 6 м, 8 м и 10 м переплавлены в один куб. Чему равно ребро этого куба.

Решение:

Пусть даны три латунных куба со сторонами 6 м, 8 м и 10 м (Рис.7). Найдем объем каждого куба:

V₁₀ = 10 3 = 1000 м 3

Отсюда следует, что общий объем должен быть равен:

V_общ = V₆ + V₈ + V₁₀ = 216 + 512 + 1000 = 1728 м 3

Следовательно, сторону куба можно найти из формулы:

а = 3 = 3 = 12 м.

Рис.7 Задача. Три латунных куба 6 м, 8 м и 10 м.

Пример 2

Решение:

Пусть дан прямоугольный параллелепипед, измерения которого равны 3 м, 4 м и 5 м (Рис.8). Найдем его площадь поверхности и объем.

S₁ = 2 * ((5 * 4) + (5 * 3) + (4 * 3)) = 94 м 2

V₁ = 5 * 4 * 3 = 60 м 3

S₂ = 2 * ((5 + х) * (4 + х) + (5 + х) * (3 + х) + (4 + х) * (3 + х)) = 94 + 54 = 148

Отсюда следует, что измерения увеличенного бруска составляют 4 м, 5 м и 6 м.

Отсюда, V₂ = 6 * 5 * 4 = 120 м 3

Т.е. объем увеличится вдвое.

Рис.8 Задача. Измерения прямоугольного бруска.

Пример 3

Решение:

Пусть дан прямой параллелепипед, в основании которого лежит ромб (Рис.9). Обозначим несколько переменных. h = AA’, a = AO, b = OD. Тогда составим следующие соотношения:

Третье уравнение решим относительно h и подставим во второе, затем второе уравнение подставим в первое:

Отсюда, а = 1 м, b = 1 / 2 м, h = 3 м.

Следовательно, объем параллелепипеда равен:

Пример 4

Боковые ребра наклонной треугольной призмы равны 15 м, а расстояние между содержащими их параллельными прямыми 26 м, 25 м и 17 м. Найдите объем призмы.

Решение:

Пусть дана наклонная треугольная призма (Рис.10). Боковое ребро AA’ = 15 м, PC = 25 м, PE = 17 м, EC = 26 м. Сечение РЕС перпендикулярно боковым ребрам. Найдем площадь треугольника РЕС по формуле Герона:

Так как треугольник РЕС лежит в плоскости, которая перпендикулярна ребрам призмы, то его следует рассматривать как проекцию треугольника АВС на плоскость сечения. Проведем прямую а, перпендикулярную стороне АВ. Опустим перпендикуляры ОC и TС к прямой а. Следовательно, угол ТСО = α и будет угол между плоскостями. Таким образом площадь треугольника АВС можно найти из формулы:

Рис.10 Задача. Боковые ребра наклонной треугольной призмы.

Таким образом, объем призмы можно найти по формуле:

Пример 5

Решение:

Пусть дана треугольная пирамида (Рис.11). AC = ВС = 6 м, АB = 8 м, SA = SB = SC = 9 м. Найдем площадь основания АВС по формуле Герона:

S_ABC = 8 м 2

Найдем радиус описанной окружности:

R = ОС = AB * BC * AC / 4S = 6 2 * 8 / 4 * 8 = 9 / м

По теореме Пифагора найдем SO:

SO = 18 / м

Теперь объем пирамиды найдем по формуле:

Источник

Что такое равновеликий куб?

Как определить что фигуры равновеликие?

Равновеликие фигуры — плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры — фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие равносоставленности применяется только к многоугольникам и многогранникам.

Что такое равновеликие фигуры?

равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрического тела с одинаковыми объёмами. * * * РАВНОВЕЛИКИЕ ФИГУРЫ РАВНОВЕЛИКИЕ ФИГУРЫ, плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами …

Как доказать Равносоставленность?

1 Равносоставленность Две фигуры называются равносоставленными, если они могут быть разрезаны на одинаковое число попарно равных фигур. Из свойств площади следует, что равносоставленные фигуры равновелики.

Что значит ребро Равновеликого Куба?

Ребро куба равно 1. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 16, 27. Найдите ребро равновеликого ему куба. Равновеликий куб – это куб, объём которого равен объёму параллелепипеда.

Какие бывают равновеликие фигуры?

РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры, имеющие равные площади, или пространственные фигуры (тела), имеющие равные объемы.

Что такое равновеликий многоугольник?

Определение равновеликих многоугольников

Равновеликие многоугольники – это многоугольники, площади которых равны.

Что такое Равносоставленные фигуры примеры?

РАВНОВЕЛИКИЕ И РАВНОСОСТАВЛЕННЫЕ ФИГУРЫ — две фигуры в R2, имеющие равные площади и соответственно два многоугольника M1 и М 2 такие, что их можно разрезать на многоугольники так, что части, составляющие М 1, соответственно конгруэнтны частям, составляющим М 2.

Что такое Равносоставленные фигуры 3 класс?

Равносоставленные фигуры – это те, которые можно составить (способом приложения) из одного и того же набора плоских фигур, при этом все фигуры набора должны участвовать в составлении.

Что значит что фигуры Равносоставлены?

Равносоставленность — отношение между фигурами определённого типа (например, многогранниками). Означает, что одну фигуру можно разбить на более мелкие куски, из которых можно составить другую фигуру.

Каким свойством обладают Равносоставленные фигуры?

Каким свойством обладают равносоставленные фигуры? Равносоставленные фигуры имеют равные площади.

Какие многогранники называются Равносоставленными?

Какие Параллелограммы называют равновеликими?

Как найти объем параллелепипеда формула?

Источник

Равновеликие фигуры

Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.

Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами). Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).

Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.

1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.

То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если

2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.

Площадь квадрата S=3²=9.

Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если

3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.

Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Площадь. Равновеликие фигуры

Разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат.

Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику.

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

Достроим треугольник до прямоугольника. Площадь треугольника равна половине площади прямоугольника.

Проведем через середину боковой стороны трапеции прямую, параллельную второй боковой стороне. Площадь трапеции равна площади полученного параллелограмма.

Перекраивание трапеции в равносоставленный треугольник:

Пло­щадь тра­пе­ции с ос­но­ва­ни­я­ми длин a и b и дли­ной вы­со­ты h рав­на S=(a+b)/2•h. Убе­дить­ся в этом мож­но вос­поль­зо­вав­шись фор­му­лой для вы­чис­ле­ния пло­ща­ди тре­уголь­ни­ка. Для это­го необ­хо­ди­мо разре­зать тра­пе­цию на та­кие ча­сти, из ко­то­рых мож­но со­ста­вить треугольник.

Разре­жем тра­пе­цию вдоль ли­нии, со­еди­ня­ю­щей вер­ши­ну с се­ре­ди­ной проти­во­по­лож­ной бо­ко­вой сто­ро­ны. По­вер­нём от­ре­зан­ный тре­уголь­ник до того момен­та, ко­гда оба ос­но­ва­ния тра­пе­ции ока­жут­ся на од­ной прямой. Убедитесь, что две ча­сти бо­ко­вой сто­ро­ны при этом ля­гут на од­ну прямую, то есть, получится дей­стви­тель­но тре­уголь­ник.

Одна из сторон получив­ше­го­ся тре­уголь­ни­ка име­ет дли­ну, рав­ную сум­ме длин оснований трапе­ции, а дли­на вы­со­ты тре­уголь­ни­ка, про­ве­дён­ной к этой стороне, сов­пада­ет с вы­со­той тра­пе­ции.

Один из способов подсчё­та пло­ща­ди тре­уголь­ни­ка со­сто­ит в на­хож­де­нии половины произве­дения дли­ны сто­ро­ны на дли­ну вы­со­ты, опу­щен­ную на эту сторону. При­ме­нение это­го спо­со­ба и да­ёт при­выч­ную фор­му­лу площа­ди трапеции.

Модель мож­но сде­лать из доски толщиной около 10 мм. Для удобства демон­стра­ции две ча­сти, на которые она разрезает­ся, удобно со­еди­нять между собой при по­мо­щи маг­ни­тов.

Равносоставленность

Равновеликие многогранники не всегда являются равносоставленными. Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — так называемая теорема Дена.

Источник