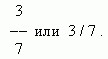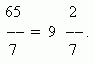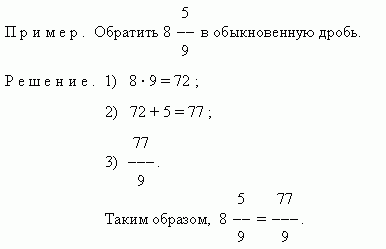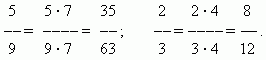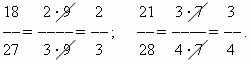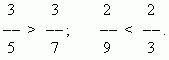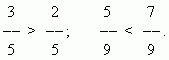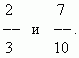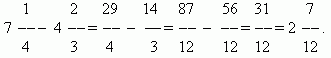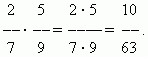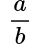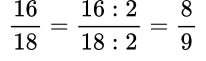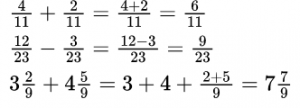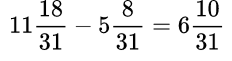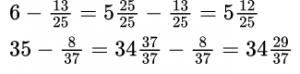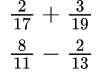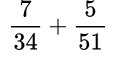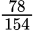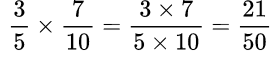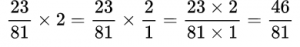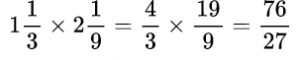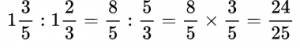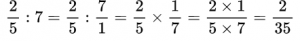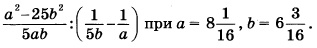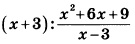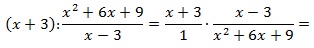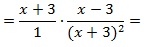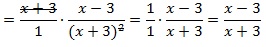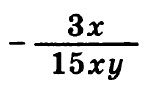Что такое равные части дроби

Умножение дробей. Деление дробей.

Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.

Использованное здесь преобразование называется приведением дробей к общему знаменателю.

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.

Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.

Источник

Математика. 5 класс

Конспект урока

Перечень рассматриваемых вопросов:

– числитель, знаменатель обыкновенной дроби;

– сократимая, несократимая дробь;

– основное свойство дроби.

Дробь в математике – это число, состоящее из одной или нескольких равных частей (долей) единицы.

Правильные дроби – это дроби, в которых числитель меньше знаменателя.

Несократимая дробь – это дробь, в которой числитель и знаменатель являются взаимно простыми числами (имеют только один общий делитель – 1).

Сократимая дробь – это дробь, у которой числитель и знаменатель имеют общий положительный делитель, не равный нулю и единице.

1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

«Все, что без этого было темно, сомнительно и неверно, математика сделала ясным, верным и очевидным», – сказал Михаил Васильевич Ломоносов.

Эти слова как нельзя кстати походят к теме нашего занятия, на котором мы будем устанавливать между, казалось бы, разными дробями равенство, хоть и не вполне очевидное с первого взгляда.

Итак, выясним, какие дроби можно назвать равными.

Для начала нарисуем отрезок. Далее разделим его на две части. Затем каждую из половинок разделим ещё на две части.

Получается, что весь отрезок поделён на четыре части. Если теперь сложить две части из четырёх, то получится ровно половина отрезка, которая в виде обыкновенной дроби будет записана как одна вторая.

Получается, что одна вторая это тоже самое, что и две четвёртых, т. е. это равные дроби.

Возьмём торт и разделим его на 10 частей.

Половина торта – это 5 частей. В виде обыкновенной дроби получается, что частям торта. Отсюда получается так называемое основное свойство дроби, которое заключается в следующем: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

С помощью этого свойства всегда получаются равные дроби. Например,

Аналогично, представим семь в виде дроби:

Если возьмём число один, представим его в виде дроби, то получим:

Получается, что две равные дроби являются различными записями одного и того же числа.

Это свойство можно применить и в обратном порядке, в этом случае говорят, что дробь можно сократить. Если числитель и знаменатель дроби имеют общий множитель, то дробь можно сократить на этот множитель, т. е. разделить на него числитель и знаменатель.

В этом случае тоже получается равная дробь. Такие дроби называются сократимыми.

Сократимая дробь – это дробь у которой числитель и знаменатель имеют общий положительный делитель, не равный нулю и единице. Например,

Рассмотрим ещё один пример, возьмём дробь :

Стоит отметить, что общий множитель числителя и знаменателя можно найти как их НОД. Например,

Стоит отметить, что сокращать дроби можно постепенно, эти действия всё равно приведут к нужному результату.

Но дроби не всегда можно сократить.

Если числитель и знаменатель дроби являются взаимно простыми числами (имеют только один общий делитель – 1), то такая дробь называется несократимой.

Например, ; – несократимые дроби.

Решим задание, связанное с сокращением дробей.

Укажите все общие делители, НОД числителя и знаменателя дроби и сократите дробь.

Решение: начнём с того, что определим общие делители числителя и знаменателя дроби, разложив их на множители:

Источник

Обыкновенные дроби

теория по математике 📈 числа и вычисления

Обыкновенная дробь – это запись числа в виде:

где число a называют числителем, а число b – знаменателем дроби.

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Пример №1. У первой дроби можно разделить числитель и знаменатель на одно и то же число 14, и получится равная ей дробь. Или как у второй дроби можно умножить числитель и знаменатель на одно и то же число, допустим, на 5.

Сократить дробь – значит разделить числитель и знаменатель на одно и то же число.

Пример №2. Чтобы сократить данную дробь надо вспомнить признаки делимости и увидеть, что числитель и знаменатель дроби — четные числа, значит, их можно разделить на 2, то есть дробь сокращается на 2:

Пример №3. По признаку делимости числитель и знаменатель делятся на 5, значит, сокращается данная дробь на 5.

Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями

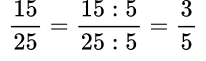
При сложении (вычитании) обыкновенных дробей с одинаковыми знаменателями нужно знаменатель оставить тем же, а числители сложить (вычесть). Если дроби смешанные, то отдельно складывают (вычитают) целые части.

Решения можно записывать короче, выполняя устно сложение или вычитание целых частей, а также – числителей.

Вычитание обыкновенной дроби из целого числа

Чтобы вычесть дробь из единицы, нужно единицу представить в виде неправильной дроби, числитель и знаменатель которой равны знаменателю вычитаемой дроби.

Пример №5. Представляем единицу в виде дроби и получаем вычитание дробей с одинаковыми знаменателями (числители можно вычесть устно).

Вычитание обыкновенной дроби из бóльшего числа

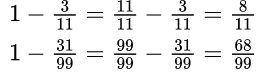
Чтобы вычесть обыкновенную дробь из числа, большего 1, необходимо представить эту дробь в виде смешанного числа, числитель и знаменатель которой равны также знаменателю вычитаемой дроби.

Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание дробей с разными знаменателями требует предварительного приведения дробей к общему знаменателю. Существуют несколько приемов, которыми можно воспользоваться для нахождения общего знаменателя.

Нахождение общего знаменателя

Наименьшее общее кратное (НОК) – это наименьшее число, которое делится без остатка на данные знаменатели одновременно. Обычно его находят устно при выполнении действий с дробями.

Правило нахождения НОК рассмотрим на примере чисел 12 и 15. Пример №7. 1. Нужно разложить на простые множители каждое число:

2. Затем найти одинаковые множители (подчеркиваем):

В данном случае это только множитель 3.

3. Взять одно из данных чисел и домножить на оставшиеся (не подчеркнутые) множители другого числа:

12 домножаем на 5: 12×5=60, или

15 домножаем на 2 и 2: 15×2×2=60

Таким образом, НОК =60. Обычно достаточно просто внимательно посмотреть на числа и в уме подобрать для них НОК.

Перемножение знаменателей. Приём №2.

Нам необходимо просто перемножить знаменатели. Обычно этот прием используется тогда, когда даны простые числа (которые делятся на 1 и на само себя) и на множители их не разложить.

Пример №8.

Для нахождения общего знаменателя в первом случае: 17×19=323, во втором: перемножаем 11 и 13, получаем 143.

Последовательный подбор. Приём №3.

Данный способ можно применить для небольших чисел устно: возьмем больший из знаменателей, умножим его на 2 и проверим, делится ли это число на второй знаменатель. Если нет, то умножим последовательно на 3, 4 и проверим аналогично.

Пример №9. Возьмем число 51, умножим на 2, получим 102 — видим, что 102 делится на 34, поэтому 102 и будет общий знаменатель.

После того, как мы научились находить общий знаменатель, приступаем непосредственно к алгоритму сложения (или вычитания) обыкновенных дробей с разными знаменателями.

Находим общий знаменатель. Можно использовать прием, когда умножаем 11 и 14, так как 11 — простое число. Следовательно, общий знаменатель равен 154. Находим дополнительный множитель к каждому числителю:

Выполняем умножение в числителе: Выполняем сложение дробей с одинаковыми знаменателями:

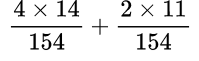
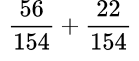
Умножение обыкновенных дробей

При умножении обыкновенных дробей получают дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

При умножении обыкновенной дроби и целого числа необходимо целое число представить в виде дроби, числитель которой равен этому числу, а знаменатель равен 1 (что по сути означает перемножение числителя единственной первой дроби и целого числа, знаменатель же остается от первой дроби, так не меняется при умножении на единицу).

Если даны смешанные дроби, то необходимо сначала смешанную дробь перевести в неправильную, а затем выполнить умножение.

Пример №11. Здесь числитель 3 умножили на числитель 7, знаменатель 5 на знаменатель 10.

Пример №12. Случай, когда мы находим произведение дроби и целого числа. Целое число представили в виде дроби со знаменателем 1.

Пример №13. Нам даны смешанные дроби, переводим их в неправильные для выполнения умножения.

Деление обыкновенных дробей

При делении обыкновенных дробей необходимо делимое (то есть первую дробь) умножить на перевернутую вторую дробь, то есть дробь, обратную второй.

Если даны смешанные числа, то перед выполнением деления их необходимо перевести в обыкновенные неправильные дроби.

Если дробь нужно разделить на целое число, то его сначала нужно представить в виде дроби, а затем выполнить деление по правилу.

Пример №14. Делимое умножаем на число, обратное делителю. 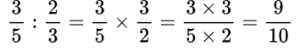Пример №15. Смешанные дроби сначала переводим в неправильные, а затем выполняем деление.

Пример №16. Деление дроби на целое число, где целое число 7 представлено в виде обыкновенной дроби.

Найдите значение выражения:

Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

теперь переходим от деления дробей к их умножению:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:

сокращаем выражение на (a–5b): Представим числовые значения для a и b в виде неправильных дробей (для удобства вычислений): Подставим полученные значения в выражение и найдем конечный результат: Ответ: 39

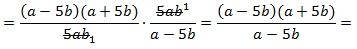
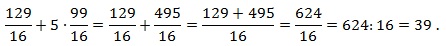
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения при x = 12:

Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:

далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):

теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:

Подставляем числовое значение для х в полученное выражение и находим результат:

Ответ: 0,6

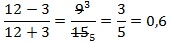
pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения

В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:

Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:

Вычислим её значение, подставив числа из условия:

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:

Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:

5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x

Тогда дробь примет вид:

Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y

Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Найдите значение выражения:

В данном случае, в отличие от первого, мы будем упрощать выражение вынося за скобки, а не раскрывая их.

Сразу можно заметить, что b присутствует у первой дроби в числителе, а у второй — в знаменателе, поэтому можем их сократить. Семь и четырнадцать тоже сокращаются на семь:

Далее выносим из числителя второй дроби a:

Подставляем значение a = 13:

pазбирался: Даниил Романович | обсудить разбор | оценить

Какое из данных ниже чисел является значением выражения?

Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?

Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.

После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:

Суммарно наши действия выглядят так:

pазбирался: Даниил Романович | обсудить разбор | оценить

Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:

1/21 + 1/28 = 4/84 + 3/84

Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:

1 / ( 7 / 84 ) = 1 •84/7 = 84/7

Далее остается поделить 84 на 7:

pазбирался: Даниил Романович | обсудить разбор | оценить

Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.

Проведя вычисления в скобках, получим:

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник