Что такое равные треугольники в геометрии 7

Что такое равные треугольники в геометрии 7

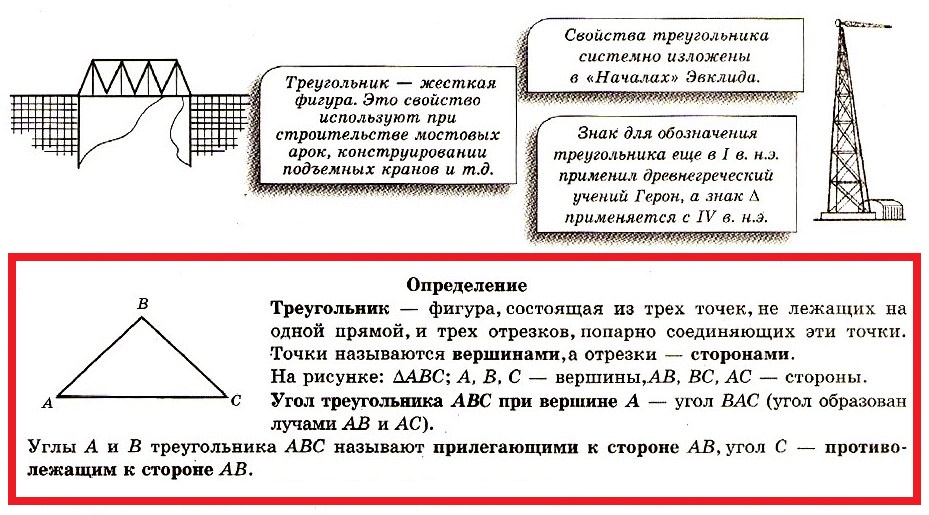
Треугольник — фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами.

Треугoльник — жесткая фигура. Это свойство используют при строительстве мостовых арок, конструировании подъемных кранов и т.д. Свойства треугольника системно изложены в «Началах» Эвклида. Знак для обозначения треугольника еще в I в. н.э. применил древнегреческий учений Герон, а знак Δ применяется с IV в. н.э.

Медиана, биссектриса и высота треугольника

Равные треугольники

Аксиома существования треугольника, равного данному.
Каким бы ни был треугольник, существует треугольник, равный ему в заданном расположении относительно данной полупрямой.

Свойства равных треугольников
1. В равных треугольниках соответствующие стороны равны.
2. В равных треугольниках соответствующие углы равны.
3. Периметры равных треугольников равны.
4. Площади равных треугольников равны.
5. Против равных сторон лежат равные углы.
6. Против равных углов лежат равные стороны.

Признаки равенства треугольников

Дополнительные признаки равенства
• Если две стороны и медиана, проведенная к третьей стороне треугольника, соответственно равны двум сторонам и медиане, проведенной к третьей стороне другого треугольника, такие треугольники равны.
• Если два угла и высота,проведенная к стороне, к которой прилегают эти углы, одного треугольника, соответственно равны двум углам и высоте, проведенной к стороне, к которой прилегают эти углы, другого треугольника, то такие треугольники равны.
• Если сторона, высота и медиана, проведенные к стороне одного треугольника, соответственно равны стороне, высоте и медиане, проведенным к этой стороне другого треугольника, то эти треугольники равны.
• Если медиана и углы, на которые она делит угол, одного треугольника, соответственно равны медиане и углам,на которые она делит угол, другого треугольника, эти треугольники равны.

Это конспект по теме «Треугoльник. Равенство треугольников». Выберите дальнейшие действия:

Источник

Признаки равенства треугольников

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Равные треугольники

Всего получено оценок: 302.

Всего получено оценок: 302.

Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.

Определение

Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.

Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.

Признаки равенства

Выделяют три признака равенства треугольников:

1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.

Рис. 1. Первый признак равенства

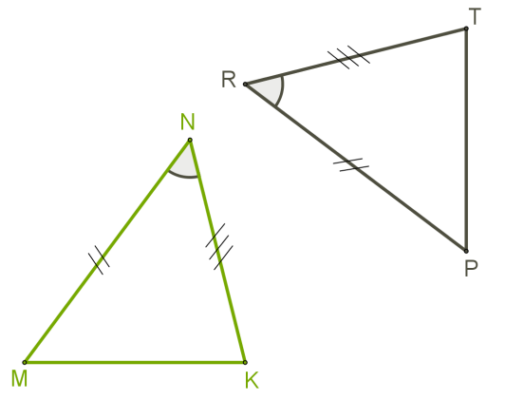
2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.

Рис. 2. Второй признак равенства

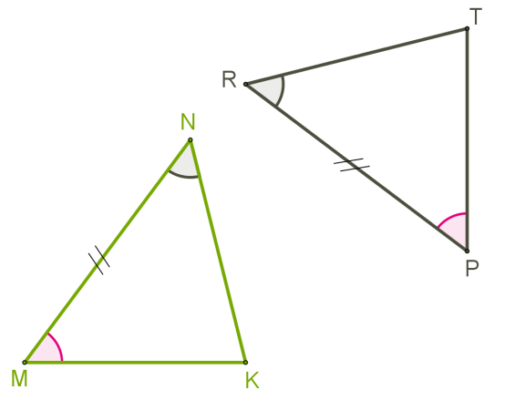
3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.

Кроме того, стоит выделить некоторые свойства:

Алгоритм доказательства равенства фигур

Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.

Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.

Пример

Решение:
Стоит обратить внимание на рисунок

Рис. 3. Два треугольника

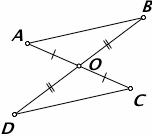
Что мы узнали?

Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.

Источник

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, которые соединены между собой отрезками.

Периметр треугольника – это сумма длин всех его сторон.

Стороны треугольника– отрезки, соединяющие вершины треугольника.

Равные треугольники –треугольники, которые можно совместить наложением.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Теоретический материал для самостоятельного изучения.

Вы уже познакомились с основными геометрическими фигурами:

Рассмотрим геометрическую фигуру, которая также является одной из основополагающих– треугольник.

Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, которые соединены между собой отрезками.

Точки, с которых начиналось построение, называются вершинами треугольника.

Отрезки, соединяющие вершины треугольника, называются сторонами треугольника.

А, В, С – вершины треугольника АВС.

АВ, ВС, СА – стороны треугольника АВС.

∠А,∠В,∠С – углы треугольника АВС.

Периметр треугольника – это сумма длин всех его сторон.

Рассмотрим виды треугольников.

Их можно разделить по виду и соотношению углов, а также по соотношению сторон.

По углам треугольник может быть:

– остроугольным, если все его углы являются острыми, (т.е. меньше 90°).

– тупоугольным, если один из его углов тупой(т.е. больше 90°).

– прямоугольным, если один угол 90° (т.е. прямой).

По сторонам треугольник бывает:

– разносторонний, если все его стороны имеют различную длину;

– равнобедренный, если две его стороны равны между собой;

– равносторонний,если у него все три стороны равны между собой.

Напомним, что две фигуры, в том числе и треугольник, можно сравнить. ∆ АВС = ∆ А₁В₁С₁

Два треугольника называются равными, если их можно совместить наложением. При этом попарно совмещаются вершины, углы и стороны треугольников.

Следует помнить, что если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам (сторонам и углам) другого треугольника.

Свойство равных треугольников.

В равных треугольниках против соответственно равных сторон лежат равные углы. Обратное утверждение тоже верно: против соответственно равных углов лежат равные стороны.

Равенство треугольников также можно установить, не производя наложения фигур друг на друга, а сравнивая лишь некоторые элементы этих фигур. Это станет возможным при изучении признаков равенства треугольников.

Внешний угол треугольника.

Введём определение внешнего угла треугольника.

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

У каждого угла треугольника есть два угла, смежных с ним, т.е. у треугольника шесть внешних углов.

Отметим, что при одной вершине внешние углы равны, как вертикальные.

Разбор решения заданий тренировочного модуля.

Найдите градусную меру внешнего ∠В, треугольника АВС, если ∠АВС = 60°.

По рисунку видно, что угол В внешний угол треугольника и он является смежным к углу АВС, следовательно, их сумма равна 180°.

∠В = 180° – ∠АВС = 180° – 60° = 120°

Периметр ∆АВС равен 58 см, сторона АВ = 20 см, сторона ВС >АС на 5 см. Найдите стороны ВС и АС.

Решение: Для решения задачи воспользуемся формулой периметра треугольника Р_∆АВС = АВ + ВС + АС. Обозначим сторону АС за х, тогда сторона ВС равна х + 5, составим уравнение.

5. х = 16,5 см – сторона АС.

6. 16,5 + 5 = 21,5 см – сторона ВС.

Источник

Что такое равные треугольники в геометрии 7

Треугольники: равные, равнобедренные. Первый, второй и третий признаки равенства треугольников. Перпендикуляр, высота, медиана, биссектриса, основание, вершина, боковая сторона. Свойства и признаки равнобедренного треугольника. Серединный перпендикуляр, геометрическое место точек, первая замечательная точка. Подробные доказательства теорем.

Наглядная геометрия 7 класс. Опорный конспект № 2 «Треугольники».

Треугольник — одна из самых замечательных и самых важных фигур в геометрии. Все знают, как он выглядит. Но что же такое треугольник? Допустим, что треугольник — это замкнутая ломаная из трех звеньев. Можно представить себе треугольник, сделанный из проволоки. Но известно, что у него есть площадь. Поэтому треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Представьте себе треугольник, сделанный из фанеры или вырезанный из картона.

Очень важным моментом при решении геометрических задач является нахождение равных треугольников. Очевидно, что если у двух треугольников все стороны и углы окажутся соответственно равными, то и треугольники будут равны. На практике равные треугольники определяют, прикладывая их друг к другу. Если треугольники совпадут при наложении, значит, они равны. Этот способ и позволяет дать определение равных треугольников.

Но вот, допустим, у каждого из двух треугольников есть две стороны, которые равны 5 см и 6 см, и какой-то из углов равен 50°. Можно ли утверждать, что треугольники равны? Оказывается, нет. На рисунке вы видите два треугольника с указанными размерами. Они не равны.

При каких же минимальных условиях треугольники будут равны? Существуют по крайней мере три признака равенства треугольников, когда по равенству некоторых сторон и углов можно абсолютно точно сказать, что они равны. Например, если бы угол 50° был образован сторонами длиной 5 см и 6 см, то треугольники были бы равны между собой.

Опорный конспект «Треугольники»

Треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Сумма длин всех трех сторон треугольника называется периметром. Треугольники называются равными, если совпадают при наложении. Если равные треугольники наложить так, что они совпадут, то окажется, что в равных треугольниках против равных сторон лежат равные углы, а против равных углов лежат равные стороны.

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Действительно, если наложить треугольники друг на друга равными углами, то совпадут и равные стороны. Значит, совпадут и оставшиеся две вершины.

Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Если наложить треугольники друг на друга равными сторонами, то совпадут углы, прилежащие к этим сторонам. Значит, совпадут и третьи вершины.

Перпендикуляром, опущенным из данной точки на данную прямую, называется отрезок прямой, перпендикулярной данной, проходящей через данную точку, с концами в данной точке и в точке пересечения с данной прямой. Точка пересечения называется основанием перпендикуляра.

Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, заключенный между вершиной и точкой пересечения биссектрисы угла и стороны треугольника.

Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны называются боковыми сторонами, третья сторона — основанием, вершина напротив этой стороны — вершиной равнобедренного треугольника. Причем названия «основание», «боковые стороны» и «вершина» равнобедренного треугольника сохраняются, как бы треугольник ни был расположен.

Свойства равнобедренного треугольника. 1. В равнобедренном треугольнике углы при основании равны. 2. Биссектриса равнобедренного треугольника, проведенная из вершины к основанию, является высотой и медианой.

Признак равнобедренного треугольника (по двум углам). Если в треугольнике два угла равны, то он равнобедренный.

Есть еще три признака равнобедренного треугольника. Треугольник является равнобедренным, если:

Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

Свойство точек серединного перпендикуляра. Любая точка серединного перпендикуляра равноудалена от концов отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Геометрическое место точек (ГМТ) — это множество всех точек плоскости, обладающих общим свойством. Например, все точки серединного перпендикуляра равноудалены от концов отрезка, и все точки плоскости, равноудаленные от концов отрезка, лежат на серединном перпендикуляре.

Первая замечательная точка. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке — центре описанной окружности.

Источник