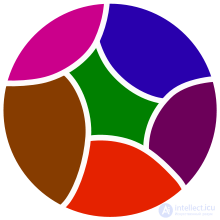
Что такое разбиение множества

Разбиение множества

Разбие́ние мно́жества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.

Определение

Пусть — произвольное множество. Семейство непустых множеств , где — некоторое множество индексов (конечное или бесконечное), называется разбиением , если:

При этом множества называются блоками или частями разбиения данного множества .

Разбиения конечных множеств

Разбиения конечных множеств, а также подсчет количества различных разбиений, удовлетворяющих тем или иным условиям, представляет особый интерес в комбинаторике. В частности, некоторые комбинаторные функции естественно возникают как количества разбиений того или иного вида.

Например, число Стирлинга второго рода представляет собой количество неупорядоченных разбиений n-элементного множества на m частей, в то время как мультиномиальный коэффициент выражает количество упорядоченных разбиений n-элементного множества на m частей фиксированного размера . Количество всех неупорядоченных разбиений n-элементного множества задается числом Белла .

Примеры

Полезное

Смотреть что такое «Разбиение множества» в других словарях:

Разбиение — В математике Разбиение единицы Разбиение множества Разбиение интервала Разбиение числа … Википедия

Разбиение графа — Пример разбиения параллельной граф схемы алгоритма логического управления. В составе блоков, отмеченных разными цветами, нет параллельных вершин Разбиение графа на подграфы (англ. Graph partition) (иногда в литературе также употребляется… … Википедия

Разбиение Вороного — Диаграмма Вороного случайного множества точек на плоскости Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к… … Википедия

Разбиение Дирихле — Диаграмма Вороного случайного множества точек на плоскости Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к… … Википедия

РАЗБИЕНИЕ — 1) Р. представление заданного множества в виде объединения системы множеств, не имеющих попарно общих точек. В дискретной геометрии часто рассматривают Р. нек рого пространства на замкнутые области, к рые покрывают все пространство и попарно не… … Математическая энциклопедия

Разбиение числа — n это представление n в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие от композиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В… … Википедия

Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия

Двоичное разбиение пространства — BSP дерево это структура данных, используемая в трехмерной графике. Аббревиатура BSP означает Binary Space Partition двоичное разбиение пространства. BSP дерево используется для эффективного выполнения следующих операций: Сортировки… … Википедия

ИЗМЕРИМОЕ РАЗБИЕНИЕ — пространства с мерой ( М,m) разбиение x. этого пространства на непересекающиеся подмножества (именуемые элементами разбиения), к рое можно получить как разбиение на множества уровня нек рой измеримой функции (с числовыми значениями) на М. Это… … Математическая энциклопедия

НЕПРЕРЫВНОЕ РАЗБИЕНИЕ — топологического пространствах покрытие пространства Xпопарно непересекающимися непустыми множествами, удовлетворяющее условию: каковы бы ни были и окрестность Uмножества Fв X, найдется окрестность Vмножества Fв X, содержащаяся в Uи являющаяся… … Математическая энциклопедия

Источник

Разбиение множества

Одной из наиболее часто встречающихся операций над множествами является операция разбиения множества на систему подмножеств.

Так, система курсов данного факультета является разбиением множества студентов факультета; система групп данного курса является разбиением множества студентов курса.

Пример. Продукция предприятия: — высший сорт, I, II, брак.

Рассмотрим некоторое множество M и систему множеств

Система множеств M называется разбиением множества M, если она удовлетворяет следующим условиям:

Тождества алгебры множеств

С помощью операций объединения, пересечения и дополнения из множеств можно составлять различные алгебраические выражения.

Если алгебраические выражения V(X,Y,Z) и S(X,Y,Z) представляют собой одно и то же множество, то их можно приравнять друг другу, получая алгебраическое тождество вида V(X,Y,Z) = S(X,Y,Z)

Дополнение к занятию «операции над множествами»

Множество элементов, принадлежащих или A, или B, называют симметричной разностью или дизьюнктивной суммой.

Для симметрической разности выполняются следующие законы:

Источник

Разбиение множества. Множества множеств.Классификация. Разбиение на классы. Примеры

разбиение множества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.

Определение

При этом множества называются блоками или частями разбиения данного множества .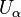

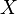
Традиционные японские символы для 54 глав « Повести о Гэндзи» основаны на 52 способах разделения пяти элементов (два красных символа представляют одно и то же разделение, а зеленый символ добавляется при достижении 54).

Разбиения конечных множеств

Разбиения конечных множеств, а также подсчет количества различных разбиений, удовлетворяющих тем или иным условиям, представляет особый интерес вкомбинаторике. В частности, некоторые комбинаторные функции естественно возникают как количества разбиений того или иного вида.

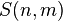
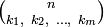
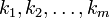
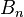
Например, число Стирлинга второго рода представляет собой количество неупорядоченных разбиений n-элементного множества на m частей, в то время какмультиномиальный коэффициент выражает количество упорядоченных разбиений n-элементного множества на m частей фиксированного размера . Количество всех неупорядоченных разбиений n-элементного множества задается числом Белла .

Примеры разбиения множеств

Мы можем рассматривать множества, состоящие из самых различных элементов. В частности, можем рассматривать множества множеств, т. е. множества, элементы которых сами суть множества. Таково, например, множество всех пар весел, имеющихся на данной лодочной станции. Множеством множеств является также множество всех спортивных команд города Н. (каждая спортивная команда есть множество составляющих ее спортсменов).

Множество всех профессиональных союзов, а также множество всех воинских частей (дивизий, полков, батальонов, рот, взводов и т. д.) данной армии являются множествами множеств. Эти примеры показывают, что множества, являющиеся элементами данного множества множеств, могут в одних случаях пересекаться, в других случаях, наоборот, не иметь общих элементов.

Так, например, множество всех партий страны есть множество попарно не пересекающихся множеств, так как гражданин не может быть одновременно членом двух политическирх партий. С другой стороны, множество всех воинских частей какой-либо армии есть пример множества множеств, некоторые элементы которого являются подмножествами других элементов: так, каждый взвод есть подмножество некоторого полка, полк есть подмножество дивизии и т. д.

Множество спортивных команд данного города состоит, вообще говоря, из пересекающихся множеств, так как одно и то же лицо может входить в несколько спортивных команд (например, в команду пловцов и в команду волейболистов или лыжников).

Замечание. Для облегчения речи иногда вместо выражения «множество множеств» употребляются как совершенно равнозначащие выражения « система множеств» или «совокупность множеств».

Понятие разбиения множества на классы

Понятие множества и операций над множествами позволяют уточнить представление о классификации.

Классификация – это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов. Классификация широко применяется в математике.

Например, натуральные числа делятся на четные и нечетные; углы бывают острые, тупые и прямые и т.д.

Любая классификация связана с разбиением некоторого множества объектов на подмножества.

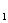
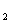
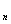
Считают, что множество Х разбито на классы Х, Х,…, Х, если:

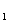
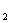
1) подмножества Х, Х,…, Х попарно не пересекаются;

2) объединение этих подмножеств совпадает с множеством Х.

Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.

Например: а) Множество треугольников Х разбито на три класса: остроугольные, прямоугольные и тупоугольные. Действительно, выделенные подмножества попарно не пересекаются, а их объединение совпадает с множеством Х; b) Из множества треугольников Х выделили подмножества равнобедренных, равносторонних и разносторонних треугольников. Так как множества равнобедренных и равносторонних треугольников пересекаются, значит, не выполнено первое условие классификации, и разбиения множества Х на классы мы не получили.

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают различными свойствами. Нас интересуют числа со свойством «быть кратным 3». Это свойство позволяет выделить из множества N подмножество, состоящее из чисел, кратных 3. Тогда про остальные натуральные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества N. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством N, то имеем разбиение данного множества на два класса.

Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – это класс объектов, обладающих данным свойством, а второй – дополнение первого класса до множества Х. Во втором классе содержатся такие объекты множества Х, которые заданным свойством не обладают. Такую классификацию называют дихотомической.

Рассмотрим ситуацию, когда для элементов множества заданы два свойства. Например, свойства натуральных чисел: «быть кратным 3» и «быть кратным 5». При помощи этих свойств из множества N можно выделить два подмножества: А – множество чисел, кратных 3 и В – множество чисел, кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 13). Разбиения на подмножества А и В в данном случае на произошло. Но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множество N. Множество I состоит из чисел, кратных 3 и 5, множество I – из чисел, кратных 3 и не кратных 5, множество III – из чисел, кратных 5 и не кратных 3, множество IV – из чисел, не кратных 3 и не кратных 5. Объединение этих четырех множеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

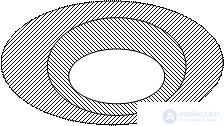
Не следует думать, что задание двух свойств элементов множества всегда приводит к разбиению этого множества на четыре класса. Например, при помощи таких двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается

на три класса (рис. 14): I – класс чисел, кратных 6; II – класс чисел, кратных 3, но не кратных 6; III – класс чисел, не кратных 3.

примеры Разбиение на классы.

Очень важный класс систем множеств получаем, если рассматриваем всевозможные разбиения какого-нибудь множества на попарно не пересекающиеся множества. Дано множество X, представленное в виде суммы попарно не пересекающихся подмножеств; множества, слагаемые нашей суммы, и являются элементами данного разбиения множества X.

Пример 1. М есть множество всех учащихся в средних школах Москвы. Множество М можно разбить на попарно не пересекающиеся подмножества, например, следующими двумя способами:

1) мы объединяем в одно слагаемое всех учащихся одной и той же школы (т. е. разбиваем множество всех учащихся по школам);

2) мы объединяем в одно слагаемое всех учащихся одного и того же класса (хотя бы и разных школ).

Пример 2. Пусть X есть множество всех точек плоскости ; возьмем на этой плоскости какую-нибудь прямую g и разобьем всю плоскость на прямые, параллельные прямой g. Множества точек каждой такой прямой и являются теми подмножествами, на которые мы разбиваем множество X.

Если данное множество X разбито на попарно не пересекающиеся подмножества, дающие в сумме множество М, то для краткости говорят просто о разбиении множества М на классы.

Задача разбиения множества чисел

Примеры разбиения множества чисел

Если дано множество S=<3,1,1,2,2,1>, допустимым решением задачи разбиения являются два множества S1= <1,1,1,2>и S2=<2,3>. Оба множества имеют сумму 5, и они являются разбиением множества S. Заметим, что это решение не уникально. S1= <3,1,1>и S2= <2,2,1>является другим решением.

Не любое мультимножество положительных целых чисел имеет разбиение на две части с равными суммами. Пример такого множества — S=<2,5>.

Подсчет разбиений

и имеют экспоненциальную производящую функцию

См. также

Источник

Разбиения множеств: размещения и перестановки, сочетания

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

РАЗБИЕНИЯ МНОЖЕСТВ

3.1. Размещения и перестановки

Рассмотрим комбинаторные конфигурации, называемые размещениями и перестановками, и соответствующие им комбинаторные числами.

На этот вопрос можно дать различные ответы в зависимости от уточнения его формулировки. Например:

Следовательно, при поиске числа различных вариантов работы конвейера может оказаться возможным:

1. Повторное нажатие кнопки, а также различный порядок нажатия кнопок. В этом случае имеется 9 вариантов:

Таким образом, при решении конкретных задач на подсчет количества способов или вариантов выбора элементов из заданного множества необходимо четко понимать, о каком способе или варианте выбора идет речь. Поэтому различные выборки получили в комбинаторике специальные названия.

Выборка называется упорядоченной, если задан порядок следования ее элементов. Поэтому две упорядоченные выборки, состоящие из одних и тех же элементов, но отличающиеся порядком их следования, являются различными.

Например, (10, 7) – размещением без повторений является (10, 7) – выборка из множества цифр.

Примечание. Составляя выборки с повторениями, обычно предполагают, что выбор элементов из данного множества производится с возвращением, т.е. считают, что выбранный из множества элемент сразу же возвращается назад или автоматически замещается таким же элементом.[10]

В силу теоремы 3.1.1.

Задача 3.1.4. В областном конкурсе СТЭМов принимают участие 9 студенческих театров. Порядок их выступлений определяется жеребьёвкой. Сколько существует вариантов в определении порядка выступления?

Задача 3.1.5. Сколькими способами официант можно рассадить 9 посетителей за круглым столом, если учитывать только порядок соседей?

Таким образом, мультимножество отличается от множества тем, что один и тот же элемент () может повторяться в нем раз.

Рассмотрим мультимножество, в котором элемент повторяется раз, элемент – раз, и т.д., элемент – раз. Число называется числом элементов мультимножества.

Задача 3.1.6. С колько различных перестановок с повторениями букв можно сделать в слове «КОЛОБОК».

В общем случае справедлива

Теорема 3.1.3. Число перестановок из n элементов с повторениями, в каждой из которых элемент повторяется раз, элемент – раз, и т.д., элемент – раз вычисляется по формуле

Перестановки совокупностей из одинаковых элементов в (*) можно делать независимо друг от друга. Поэтому по обобщенному правилу произведения можно способом переставить друг с другом элементы перестановки (*) так, что она не изменится.

Ясно, что в любой другой отличной от (*) упорядоченной последовательности, содержащей все n элементов данного мультимножества, можно делать независимо друг от друга перестановки способами так, что она не изменится. Поэтому число всех искомых перестановок с повторениями в раз меньше, чем число всех перестановок из различных элементов. ■

Задача 3.1.7. Сколько анаграмм можно составить из слова «математика»? (Анаграммой называется «слово», полученное перестановками букв данного слова, независимо от того, имеет оно или не имеет смысловое значение.)

3.2. Сочетания

Например, если из десяти сотрудников отдела нужно выбрать троих делегатов на заводскую конференцию, то порядок выбора сотрудников не имеет значения. Поэтому любая тройка выбранных сотрудников является (10, 3) – сочетанием без повторений. Но если из десяти цифр на телефонном аппарате необходимо набрать трехзначный телефонный номер, все цифры которого различны, то порядок набора цифр уже имеет значение. Поэтому тройка цифр такого телефонного номера не является сочетанием, а будет (10, 3) – размещением без повторений.

Умножая на числитель и знаменатель этой дроби, получим

Примечание. Формула связывает число сочетаний и размещений из n элементов по без повторений и число перестановок из элементов.

Задача 3.2.1. В областном конкурсе СТЭМов участвует
9 театров. Сколькими способами жюри конкурса может выбрать трех участников финала?

Задача 3.2.2. Доказать, что для всех справедливо равенство:

Задача 3.2.3. Доказать, что при

Задача 3.2.4. Доказать, что для всех справедливо равенство

Сочетания с повторениями. Для подсчета числа сочетаний из n элементов по r с повторениями используется

Задача 3.2.5. В цветочном магазине имеется 7 различных сортов цветов. Сколькими способами можно составить букет из 5 цветов?

Задача 3.2.6. Сколькими способами 25 человек могут заказать на десерт по порции мороженого, если в ассортименте кафе имеется 5 сортов мороженого и выбор каждого сорта не ограничен?

В тех случаях, когда выборка происходит из мультимножества, следует быть осторожным. Здесь выбор предметов может оказаться ограниченным. Рассмотрим задачу.

Задача 3.2.7. Сколькими способами можно составить букет из 5 роз, если в наличии имеется 5 одинаковых красных, 4 одинаковых белых и 3 одинаковых желтых розы?

Нетрудно, однако, перебрать все возможные варианты составления букета. Буквы К, Б и Ж в выборках будут означать включение в букет красной, белой и желтой розы соответственно. Последовательно составим все возможные букеты с 5, 4, 3, 2, 1 и 0 красными розами.

ККБББ, ККББЖ, ККБЖЖ, ККЖЖЖ;

КББББ, КБББЖ, КББЖЖ, КБЖЖЖ;

Источник

Электронная библиотека

Напомним, что разбиением множества A называется семейство <A_i> его непустых попарно непересекающихся подмножеств, таких, что È_iA_i = A. Подмножества A_i называются блоками разбиения. Если в семействе учитывается порядок подмножеств, и если допускаются пустые блоки, то оно называется упорядоченным разбиением.

Упорядоченные разбиения и обобщенный бином Ньютона

Подмножество A₁ можно выбрать способами. Подмножество A₂ выбирается из оставшихся n-k₁ элементов, его можно будет выбрать способами. Подмножество A₃ можно будет выбрать способами, и т.д. Выбор подмножества A_m определен предшествующими подмножествами. Отсюда получаем:

Поскольку n – k₁ – … – k_m-1 = k_m, то после сокращения дроби получаем нужное равенство.

Рассмотрим как ящики сомножители произведения:

Разбиения и перечисление сюръекций

Пусть <B₁, …, B_k> – разбиение множества X, состоящего из n элементов. Обозначим через P_k(X) множество разбиений X на k блоков, а через P(X) – множество всех

Каждому разбиению мы сопоставили отношение эквивалентности и заметили, что разбиения составляют решетку относительно включения соответствующих отношений эквивалентности. Отсюда множество разбиений будет решеткой относительно неравенства p£s Û, каждый блок B Î s является объединением некоторых блоков из p.

Число S(4,2) равно 7, ибо все разбиения множества <1,2,3,4, 5, 6, 7>на два блока исчерпываются следующими множествами:

Имеют место следующие свойства чисел Стирлинга второго рода:

2. Сколькими способами можно раскрасить 4 полосы флага в 7 цветов, так, чтобы, по крайней мере, две полосы имели одинаковый цвет?

3. Сколькими способами можно раскрасить 4 полосы флага в 7 цветов, так, чтобы рядом находящиеся полосы имели различные цвета?

4. Сколько перестановок p <1,2, …, 5> ® <1,2, …, 5> удовлетворяют условию p(1)¹ 2?

5. В соревновании принимают участие 8 спортсменов. Сколь­кими способами могут быть разделены медали (золотые, се­ребряные и бронзовые)?

8. Сколько чисел между 1000 и 10000 состоят из различных цифр?

9. Сколько семизначных чисел (не начинающихся с 0) состоят из различных цифр?

10. Доказать тождества непосредственно из определения числа :

11. Из содержащей 52 карты колоды вынимают 10 карт. Какова вероятность, что среди них окажется

1) хотя бы один туз? Ответ:

2) ровно один туз? Ответ:

3) не менее двух тузов? Ответ:

4) ровно два туза? Ответ:

12. Из содержащей 52 карты колоды вынимают 10 карт. Какова вероятность, что среди них окажется

1) 4 туза, 2 короля, 3 дамы;

2) 2 туза, 2 короля, 2 дамы;

3) 1 туз, 1 короля, 2 дамы, 3 десятки;

4) 4 туза, 4 короля, 2 дамы;

5) 2 туза, 3 короля, 1 дама, 1 десятка;

6) 3 туза, 2 короля, 4 дамы.

13. Разложением числа m называется конечная последовательность (x₁, x₂, ×××, x_n) неотрицательных целых чисел, таких, что x₁+ x₂+ ××× + x_n = m. Сколько разложений числа 19 состоит лишь из чисел 2 и 3?

Указание. Если в разложении p двоек и q троек, то 2p + 3q = 19. Отсюда получаем следующие варианты разложения:

1. Сколько разложений числа 12 состоит из чисел 2 и 3?

2. Сколькими способами можно разложить число 1024 в произведение трех натуральных чисел, каждое из которых больше 1?

3. Сколько существует на плоскости непрерывных путей из точки (0,0) в точку (n,n) Î N ´ N, состоящих из направленных отрезков, вектора которых равны (1,0) или (0,1)?

4. Найти число непрерывных путей в декартовой плоскости, соединяющих точку (0,0) с точкой (m,n) Î N´N, проходящих через точку (p,q) и состоящих из направленных отрезков, вектора которых равны (1,0) или (0,1)?

7. Найти число возрастающих функций <1,2,3,4,5>®<1,2,3,4,5,6,7>.

8. Найти число неубывающих сюръекций <1,2,3,4,5,6,7>®<1,2,3,4,5>.

9. Найти число неубывающих функций <1,2,3,4,5>®<1,2,3,4,5>.

10. Найти количество десятичных неотрицательных целых чисел, состоящих из не более, чем n цифр, расположенных в неубывающем порядке (цифра 0 не допускается первой для ненулевых чисел). Например, при n = 2, такие числа будут равны:

11, 12, 13, 14, 15, 16, 17, 18, 19, 22, 23, …∙, 89, 99.

11. Найти количество десятичных неотрицательных целых чисел, состоящих цифр, расположенных в возрастающем порядке.

12. Найти число неотрицательных целых чисел, десятичная запись которых состоит из n разрядов и содержит все цифры, расположенные в невозрастающем порядке.

13. Какое количество m ´ n-матриц можно составить из неотрицательных целых чисел a_ij ³ 0, таких, что S a_ij = k.

14. Десять человек разбились на 5 групп по 2 человека в каждой. Скольким способами это можно сделать?

Указание. Количество упорядоченных разбиений равно 10!/(2!2!2!2!2!). При перестановках групп получаются одинаковые разбиения, отсюда искомое число равно:

1. В группе 20 студентов. Одному человеку положено выдать надбавку к стипендии в размере 1000 рублей, двум – по 500, трем – по 300. Сколькими способами это можно сделать?

2. Сколько существует шашечных позиций, состоящих из 10 белых и 10 черных шашек?

3. Сколько различных слов можно составить с помощью перестановок всех букв слова МАТЕМАТИКА. Словом называется произвольная конечная последовательность букв.

4. Оценить число шахматных позиций, содержащих все фигуры и пешки?

5. В урне находится k шаров. Каждый шар может иметь либо белый, либо черный, либо красный цвет. Какова вероятность того, что один шар белый, один – черный (а остальные красные)?

6. Найти коэффициент при в разложении степени в сумму однородных одночленов.

8. Сколько путей, составленных из направленных отрезков единичной длины, существует в трехмерной решетке из (0,0,0) в (p,q,r). Вектора отрезков равны (1,0,0), (0,1,0), (0,0,1).

Формула включения и исключения

9. Сколько чисел из принадлежащих множеству <1, 2, …, 1000> не делится ни на 10, ни на 12, ни на 9?

10. Группа из 20 студентов сдает зачеты по математике, физике и информатике. Множество студентов, сдавших математику и физику совпадает с множеством студентов, сдавших математику и информатику, и совпадает с множеством студентов, сдавших физику и информатику. Каждый студент сдал, по крайней мере, один зачет. Найти число студентов, сдавших все зачеты, если математику сдали 15, физику – 16, информатику – 17 студентов.

11. Найти число разбиений множества <1,2,3,4,5,6,7>на 3 блока.

12. Найти число разбиений множества, состоящего из 8 элементов.

14. Вывести формулу для числа сюръекций <1, 2, …, m>®<1, 2, …, n> с помощью формулы включения и исключения для подсчета числа несюръективных отображений |U₁È×××È U_n|, где U_i – множество отображений, образ которых не содержит элемент i.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник