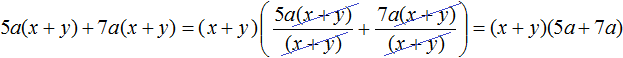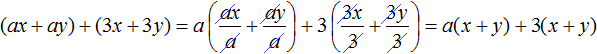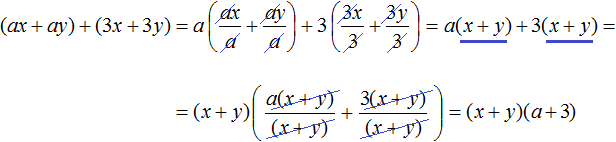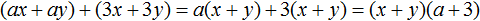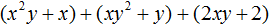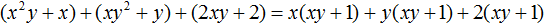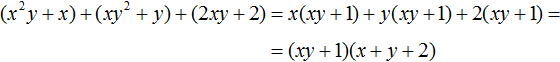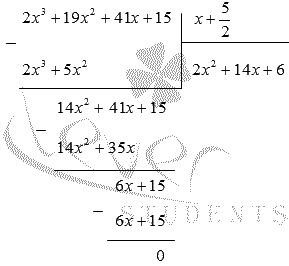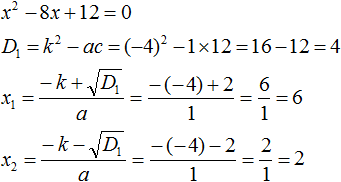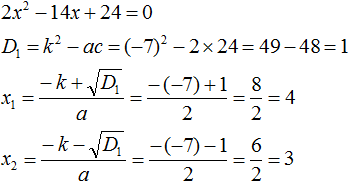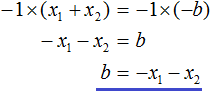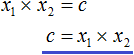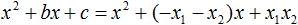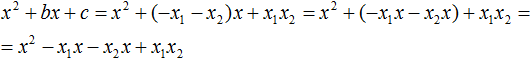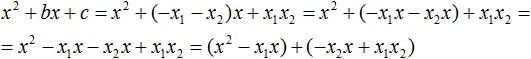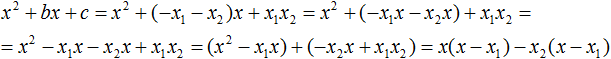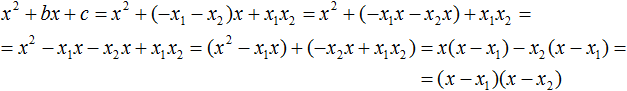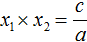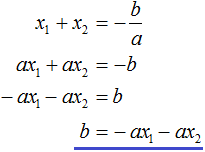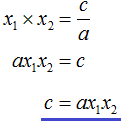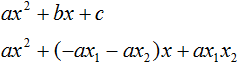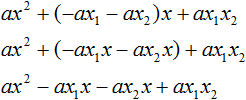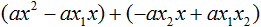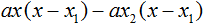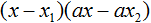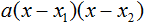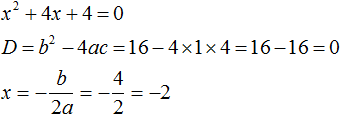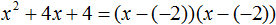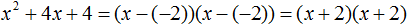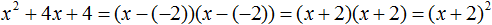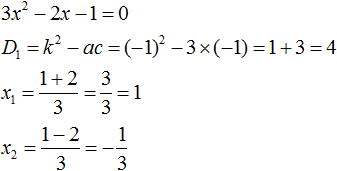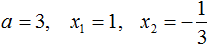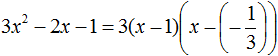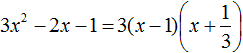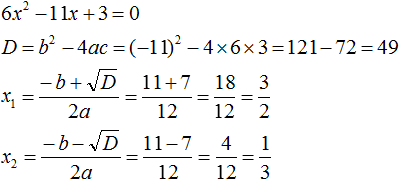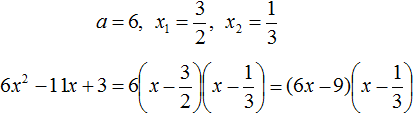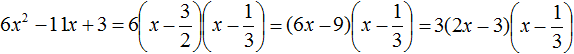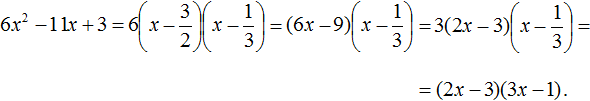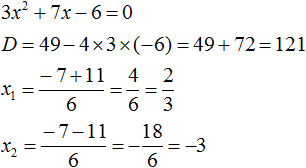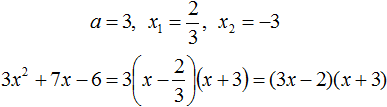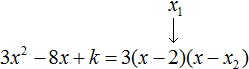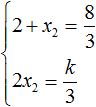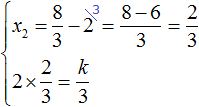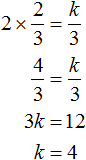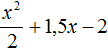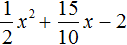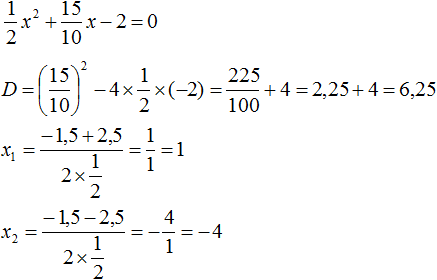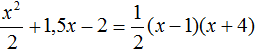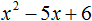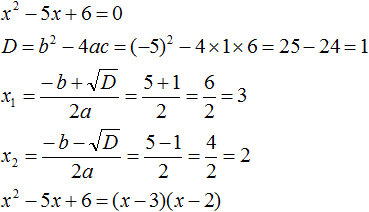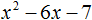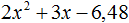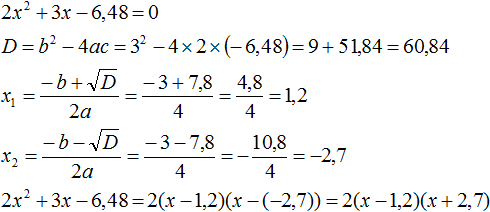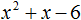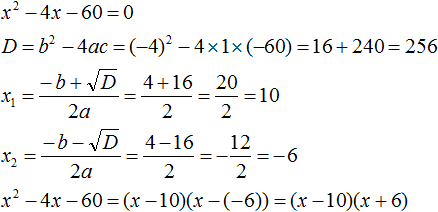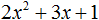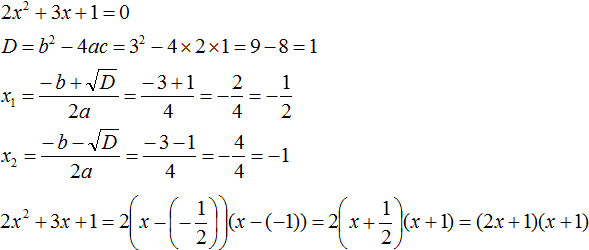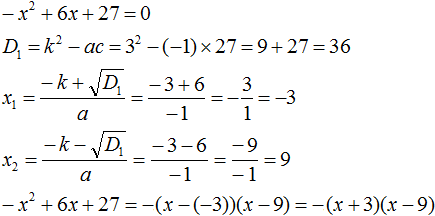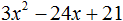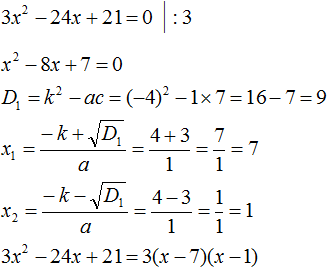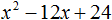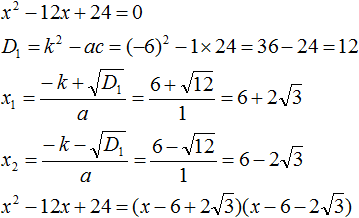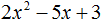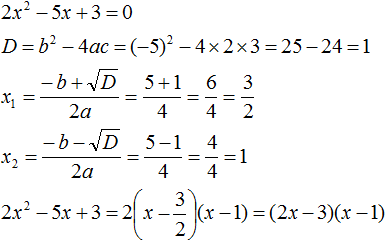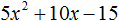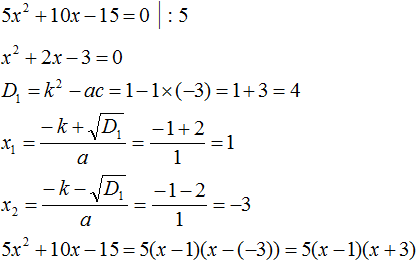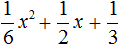Что такое разложить на множители
Разложение многочлена на множители
Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.
Примером разложения многочлена на множители является вынесение общего множителя за скобки, поскольку исходный многочлен обращается в произведение двух сомножителей, один из которых является одночленом, а другой многочленом.
Разложение многочлена на множители способом вынесения общего множителя за скобки
При вынесении общего множителя за скобки образуется произведение из двух сомножителей, один из которых является одночленом, а другой многочленом. Например:
В рамках изучения многочленов, одночлен принято считать многочленом, состоящим из одного члена. Поэтому, когда в многочлене выносится за скобки общий множитель, то говорят что исходный многочлен представлен в виде произведения многочленов.
Разложение многочлена на множители способом группировки
Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить общий множитель за эти скобки. В результате получается разложение исходного многочлена на множители, которое называют разложением на множители способом группировки.
Рассмотрим следующий многочлен:
Далее в многочлене ax + ay + 3 x + 3 y члены 3x и 3y имеют общий множитель 3. Выпишем эти члены и тоже заключим их в скобки:
Теперь соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»
Далее замечаем, что двучлен (x + y) является общим множителем. Вынесем его за скобки. Продолжаем решение в исходном примере. В результате получим:
Запишем решение покороче, не расписывая подробно, как каждый член был разделен на общий множитель. Тогда решение получится более компактным:
Пример 2. Разложить многочлен 9x + ax − 9y − ay на множители способом группировки.
В первой группе (9x − 9y) вынесем за скобки общий множитель 9. Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a
Далее вынесем за скобки двучлен (x − y)
Пример 3. Разложить многочлен ab − 3b + b 2 − 3a на множители способом группировки.
Во втором произведении b(−3 + b) в сомножителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)
Теперь вынесем за скобки общий множитель (b − 3)
Пример 4. Разложить многочлен x 2 y + x + xy 2 + y + 2xy + 2 на множители способом группировки.
Сгруппируем первый член многочлена со вторым, третий с четвёртым, пятый с шестым:
Далее замечаем, что многочлен (xy + 1) является общим множителем. Вынесем его за скобки:
Разложение многочлена на множители по формуле квадрата суммы двух выражений
Формулы сокращённого умножения, которые мы рассматривали в прошлом уроке, можно применять для разложения многочленов на множители.
Вспомним, как выглядит формула квадрата суммы двух выражений:
Поменяем местами левую и правую часть, получим:
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b) 2 представляет собой перемножение двух сомножителей, каждый из которых равен многочлену (a + b).
Пример 1. Разложить на множители многочлен 4x 2 + 12xy + 9y 2
Полностью решение можно записать так:
Пример 2. Разложить на множители многочлен x 2 + 12x + 36
Разложение многочлена на множители по формуле квадрата разности двух выражений
Как и по формуле квадрата суммы двух выражений, многочлен можно разложить на множители по формуле квадрата разности двух выражений.
Формула квадрата разности двух выражений выглядит так:
Если в этой формуле поменять местами левую и правую часть, то получим:
Поскольку правая часть это произведение двух сомножителей, каждый из которых равен (a − b), то многочлен вида a 2 − 2ab + b 2 можно разложить на множители (a − b) и (a − b).
Пример 1. Разложить на множители многочлен 9x 2 − 12xy + 4y 2
Полностью решение можно записать так:
Пример 2. Разложить на множители многочлен x 2 − 4x + 4
Воспользуемся формулой квадрата разности двух выражений:
Разложение многочлена на множители по формуле куба суммы двух выражений
Вспомним, как выглядит формула куба суммы двух выражений:
Поменяем местами левую и правую часть, получим:
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b) 3 представляет собой перемножение трёх сомножителей, каждый из которых равен многочлену (a + b).
Пример 1. Разложить на множители многочлен m 3 + 6m 2 n + 12mn 2 + 8n 3
Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб суммы двух выражений.
Первый член данного многочлена является результатом возведения в куб одночлена m
Последний член 8n 3 является результатом возведения в куб одночлена 2n
Второй член 6m 2 n является утроенным произведением квадрата первого выражения m и последнего 2n
Третий член 12mn 2 является утроенным произведением первого выражения m и квадрата последнего выражения 2n
Пример 2. Разложить на множители многочлен 125x 3 + 75x 2 + 15x + 1
Первый член данного многочлена является результатом возведения в куб одночлена 5x
Последний член 1 является результатом возведения в куб одночлена 1
Второй член 75x 2 является утроенным произведением квадрата первого выражения 5x и последнего 1
Третий член 15x является утроенным произведением первого выражения 5x и квадрата второго выражения 1
Разложение многочлена на множители по формуле куба разности двух выражений
Как и по формуле куба суммы двух выражений, многочлен можно разложить на множители по формуле куба разности двух выражений.
Вспомним, как выглядит формула куба разности двух выражений:
Если в этой формуле поменять местами левую и правую часть, то получим:
Поскольку правая часть это произведение трёх сомножителей, каждый из которых равен (a − b), то многочлен вида a 3 − 3a 2 b + 3ab 2 − b 3 можно разложить на множители (a − b), (a − b) и (a − b).
Пример 1. Разложить на множители многочлен 64 − 96x + 48x 2 − 8x 3
Прежде чем применять формулу куба разности, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб разности двух выражений.
Первый член данного многочлена является результатом возведения в куб одночлена 4
Последний член 8x 3 является результатом возведения в куб одночлена 2x
Второй член 96x является утроенным произведением квадрата первого выражения 4 и последнего 2x
Третий член 48x 2 является утроенным произведением первого выражения 4 и квадрата второго выражения 2x
3 × 4 × (2x) 2 = 3 × 4 × 4x 2 = 48x 2
Пример 2. Разложить на множители многочлен 27 − 135x + 225x 2 − 125x 3
Первый член данного многочлена является результатом возведения в куб одночлена 3
Последний член 125 является результатом возведения в куб одночлена 5x
Второй член 135x является утроенным произведением квадрата первого выражения 3 и последнего 5x
Третий член 225x 2 является утроенным произведением первого выражения 3 и квадрата второго выражения 5x
3 × 3 × (5x) 2 = 3 × 3 × 25x 2 = 225x 2
Разложение многочлена на множители по формуле разности квадратов двух выражений
Вспомним, как выглядит формула умножения разности двух выражений на их сумму:
Если в этой формуле поменять местами левую и правую часть, то получим:
Эту формулу называют разностью квадратов. Она позволяет разложить выражение вида a 2 − b 2 на множители (a − b) и (a + b).
Пример 1. Разложить на множители многочлен 16x 2 − 25y 2
Первый член 16x 2 является результатом возведения в квадрат одночлена 4x
Второй член 25y 2 является результатом возведения в квадрат одночлена 5y
Полностью решение можно записать так:
Пример 2. Разложить на множители многочлен x 2 − y 2
Чаще всего члены, из которых состоит исходная разность, являются результатами возведения во вторую степень каких-нибудь одночленов. Чтобы узнать чему в таком случае равны a и b, нужно как в первом примере представить члены исходной разности в виде одночленов возведённых в квадрат.
Полностью решение можно записать так:
Несмотря на простоту разложения по формуле разности квадратов, частые ошибки приходятся именно на эти задачи. Чтобы убедиться, что задача решена правильно, не мешает выполнить умножение в получившемся разложении. Если задача решена правильно, то должен получиться изначальный многочлен.
Проверим умножением данный пример. У нас должен получиться многочлен 4x 4 − 9y 6
Пример 4. Разложить на множители многочлен 81 − 64
Представим члены исходной разности в виде одночленов возведенных в квадрат. Далее воспользуемся формулой разности квадратов:
81 − 64 = 9 2 − 8 2 = (9 − 8)(9 + 8)
Разложение многочлена на множители по формуле сумме кубов двух выражений
Мы помним, что произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений:
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую суммой кубов двух выражений:
Пример 1. Разложить на множители многочлен 27x 3 + 64y 3
Представим члены 27x 3 и 64y 3 в виде одночленов, возведённых в куб
Пример 2. Разложить на множители многочлен 125 + 8
Представим члены 125 и 8 в виде одночленов, возведённых в куб:
Далее воспользуемся формулой суммы кубов:
125 + 8 = 5 3 + 2 3 = (5 + 2)(25 − 10 + 4)
Разложение многочлена на множители по формуле разности кубов двух выражений
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений:
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую разностью кубов двух выражений:
Пример 1. Разложить на множители многочлен 64x 3 − 27y 3
Представим члены 64x 3 и 27y 3 в виде одночленов, возведённых в куб:
Пример 2. Разложить на множители многочлен 64 − 27
Представим члены 64 и 27 в виде одночленов, возведённых в куб:
64 − 27 = 4 3 − 3 3 = (4 − 3)(16 + 12 + 9)
Пример 3. Разложить на множители многочлен 125x 3 − 1
Представим члены 125x 3 и 1 в виде одночленов, возведённых в куб:
Разложение многочлена на множители различными способами
К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.
Пример 1. Разложить на множители многочлен ax 2 − ay 2
При этом в скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим:
Пример 2. Разложить на множители многочлен 3x 2 + 6xy + 3y 2
Вынесем за скобки общий множитель 3
Разложение многочлена на множители
Для того, чтобы разложить на множители, необходимо упрощать выражения. Это необходимо для того, чтобы можно было в дальнейшем сократить. Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным.
Статья раскроет все понятия разложения, теоретические основы и способы разложений многочлена на множители.
Теория
Замечание
Корни многочлена могут повторяться. Рассмотрим доказательство теоремы алгебры, следствия из теоремы Безу.
Основная теорема алгебры
Любой многочлен со степенью n имеет как минимум один корень.
Теорема Безу
Следствие из теоремы Безу
Разложение на множители квадратного трехчлена
Отсюда видно, что само разложение сводится к решению квадратного уравнения впоследствии.
Произвести разложение квадратного трехчлена на множители.
Для выполнения проверки нужно раскрыть скобки. Тогда получим выражение вида:
После проверки приходим к исходному выражению. То есть можно сделать вывод, что разложение выполнено верно.
Чтобы найти корни, надо определить значение дискриминанта. Получим, что
Произвести разложение многочлена 2 x 2 + 1 на множители.
Теперь нужно решить квадратное уравнение 2 x 2 + 1 = 0 и найти его корни. Получим, что
Для начала необходимо решить квадратное уравнение вида x 2 + 1 3 x + 1 = 0 и найти его корни.
Получив корни, запишем
Если значение дискриминанта отрицательное, то многочлены останутся многочленами второго порядка. Отсюда следует, что раскладывать их не будем на линейные множители.
Способы разложения на множители многочлена степени выше второй
Если корень не нашли, тогда применяются другие способы разложения на множители: группировка, дополнительные слагаемые. Данная тема полагает решение уравнений с высшими степенями и целыми коэффициентами.
Вынесение общего множителя за скобки
Данный способ считается вынесением общего множителя за скобки.
Разложение на множители многочлена с рациональными корнями
Когда многочлен имеет целые корни, тогда их считают делителями свободного члена.
Так как дискриминант получаем отрицательный, значит, действительных корней нет.
Этот случай имеет место быть для дробно-рациональных дробей.
4 f ( x ) = 2 3 · x 3 + 19 · 2 2 · x 2 + 82 · 2 · x + 60 = = y 3 + 19 y 2 + 82 y + 60 = g ( y )
Когда получившаяся функция вида g ( y ) = y 3 + 19 y 2 + 82 y + 60 имеет целые корни, тогда их нахождение среди делителей свободного члена. Запись примет вид:
Перейдем к вычислению функции g ( y ) в этих точка для того, чтобы получить в результате ноль. Получаем, что
2 x 3 + 19 x 2 + 41 x + 15 = x + 5 2 ( 2 x 2 + 14 x + 6 ) = = 2 x + 5 2 ( x 2 + 7 x + 3 )
Отсюда следует, что
Искусственные приемы при разложении многочлена на множители
Рациональные корни не присущи всем многочленам. Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.
Способ группировки
Бывают случаи, когда можно сгруппировывать слагаемые многочлена для нахождения общего множителя и вынесения его за скобки.
Отсюда видно, что корней нет, необходимо использовать другой способ разложения и решения.
Необходимо провести группировку:
После группировки исходного многочлена необходимо представить его как произведение двух квадратных трехчленов. Для этого нам понадобится произвести разложение на множители. получаем, что
Простота группировки не говорит о том, что выбрать слагаемы достаточно легко. Определенного способа решения не существует, поэтому необходимо пользоваться специальными теоремами и правилами.
Заданный многочлен не имеет целых корней. Следует произвести группировку слагаемых. Получаем, что
После разложения на множители получим, что
Использование формул сокращенного умножения и бинома Ньютона для разложения многочлена на множители
Внешний вид зачастую не всегда дает понять, каким способом необходимо воспользоваться при разложении. После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.
Необходимо выполнить преобразование выражения к виду
После применения разности квадратов, получим
Рассмотрим выражение, которое находится во второй скобке. Понятно, что там коней нет, поэтому следует применить формулу разности квадратов еще раз. Получаем выражение вида
Займемся преобразованием выражения. Получаем, что
Необходимо применить формулу сокращенного умножения разности кубов. Получаем:
Способ замены переменной при разложении многочлена на множители
При замене переменной производится понижение степени и разложение многочлена на множители.
x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6
x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6 = = y + 2 y + 3 = x 3 + 2 x 3 + 3
Необходимо применить формулу сокращенного умножения суммы кубов. Получим выражения вида:
То есть получили искомое разложение.
Рассмотренные выше случаи помогут в рассмотрении и разложении многочлена на множители разными способами.
Разложение многочлена способом группировки
Основные понятия
Мы знаем, что слово «множитель» происходит от слова «умножать».
Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.
Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:
Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.
Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
5 способов разложения многочлена на множители
Способ группировки множителей
Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.
Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.
Разложить на множители методом группировки можно в три этапа:
Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.
Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.
Заметим, что в первой группе повторяется p, а во второй — d.
Вынесем в первой группе общий множитель p, а во второй общий множитель d.
Вынесем его за скобки:
Группировка множителей выполнена.
Заметим, что в первой группе повторяется u, а во второй — b.
Вынесем в первой группе общий множитель u, а во второй общий множитель b.
Заметим, что общий множитель (p + d).
Вынесем его за скобки:
Группировка множителей выполнена.
От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:
Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.
Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.
Проверим как это на следующем примере.
Разложение квадратного трёхчлена на множители
Как разложить на множители квадратный трёхчлен
В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:
Левая часть этого уравнения является квадратным трёхчленом.
Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.
Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением:
Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:
Где левая часть — исходный квадратный трёхчлен.
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:
В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
Если a равно единице (как в данном примере), то решение можно записать покороче:
Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Приравняем данный квадратный трёхчлен к нулю и решим уравнение:
Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24
Как это работает
Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.
Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:
Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:
Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c
Раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Далее замечаем, что выражение ( x − x1 ) является общим множителем. Вынесем его за скобки:
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.
Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a
Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a
Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 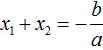
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
Скобки внутри скобок можно раскрыть. Тогда получим следующее:
При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)
Примеры разложений
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Во вторых скобках можно заменить вычитание сложением:
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
Пример 3. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби 
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
Пример 5. Разложить на множители следующий квадратный трёхчлен:
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим 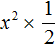
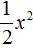
Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже