Что такое размах ряда чисел в алгебре
Среднее арифметическое, размах и мода
Вы будете перенаправлены на Автор24
Основные понятия
В качестве одной из важнейших характеристик есть средние величины. В математической статистике различают несколько видов средних величин: арифметическую, геометрическую, гармоничную, квадратичную, кубичную и другие. Все перечисленные типы средних могут быть вычислены для случаев, когда каждая из вариантов вариационного ряда встречается только один раз. Когда значения варианта повторяются разное количество раз, то вычисление средних величин называются свешенными.
Для характеристики вариационного ряда один из перечисленных типов средних выбирается не произвольно, а в зависимости от особенностей явлений, что изучается и целей, для которых среднее вычисляется.
$m-$ показатель степени, что определяет тип средней.
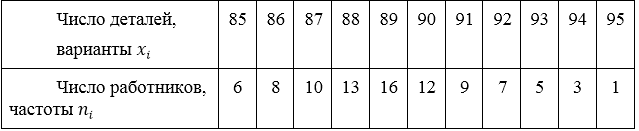
За данными про количество деталей, которые изготовили работники за смену вычислить среднее арифметической.
Вычислить среднее арифметическое.
Мода и размах
Кроме средних в статистике для описательной характеристики величины варьирующего признака пользуются показателями моды и размаха.
Мода применяют, к примеру при определении размера обуви, одежды, пользующейся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар и пр.
Модой в дискретном ряде называется варианта, которая имеет самую большую частоту (то есть повторяется наибольшое количество раз), например: имеем итоговую таблицу о продажах в магазине обуви по размерам:
В данном примере модой является 38-й размер, так как пар обуви данного размера продано больше всего, а именно 197 пар.
При равных интервалах моду внутри модального интервала можно определить за формулой:
Про моду можно сказать, что она является наиболее распространенной типичной величиной в распределении. К тому же, и мода и средняя величина характеризуют совокупность по разному, а именно мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Поэтому мода уступает средней по своему обобщающему значению, которая характеризует совокупность в целом, так как складывается под воздействием всех без исключения элементов совокупности.
Размах вариации одна из простейших мер колеблемости значений признака и являет собой разность между максимальным и минимальным значением признака:
Недостатком размаха вариации является, то, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость данного признака.
Имея ввиду то, что каждое из индивидуальных значений признака имеет отклонения от средней на некоторую величину, то мерой вариации может выступать средняя из отклонений каждой отдельной варианты от их средней.
Такими показателями является как среднее линейное отклонение так и среднее квадратическое отклонение и дисперсия.
За данным статистическим распределением определить размах.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 29 01 2021
Что такое размах ряда чисел в алгебре
Среднее арифметическое ряда чисел – это сумма данных чисел, поделенная на количество слагаемых.
Среднее арифметическое называют средним значением числового ряда.
Пример : Найдем среднее арифметическое чисел 2, 6, 9, 15.
Решение. У нас четыре числа. Значит, надо их сумму разделить на 4. Это и будет среднее арифметическое данных чисел:
(2 + 6 + 9 + 15) : 4 = 8.
Среднее геометрическое ряда чисел – это корень n-й степени из произведения этих чисел.
Пример : Найдем среднее геометрическое чисел 2, 4, 8.
Решение. У нас три числа. Значит, надо найти корень третьей степени из их произведения. Это и будет среднее геометрическое данных чисел:
3 √ 2 · 4 · 8 = 3 √64 = 4
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Пример : Найти размах чисел 2, 5, 8, 12, 33.
Решение : Наибольшее число здесь 33, наименьшее 2. Значит, размах составляет 31:
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Пример : Найти моду ряда чисел 1, 7, 3, 8, 7, 12, 22, 7, 11, 22, 8.
Решение : Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медиана.
В упорядоченном ряде чисел:
Медиана нечетного количества чисел – это число, записанное посередине.
Пример : В ряде чисел 2, 5, 9, 15, 21 медианой является число 9, находящееся посередине.
Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Пример : Найти медиану чисел 4, 5, 7, 11, 13, 19.
Решение : Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел:
Число 9 и является медианой данного ряда чисел.
В неупорядоченном ряде чисел:
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Пример 1 : Найдем медиану произвольного ряда чисел 5, 1, 3, 25, 19, 17, 21.
Решение : Располагаем числа в порядке возрастания:
1, 3, 5, 17, 19, 21, 25.
Посередине оказывается число 17. Оно и является медианой данного ряда чисел.
Пример 2 : Добавим к нашему произвольному ряду чисел еще одно число, чтобы ряд стал четным, и найдем медиану:
5, 1, 3, 25, 19, 17, 21, 19.
Решение : Снова выстраиваем упорядоченный ряд:
1, 3, 5, 17, 19, 19, 21, 25.
Посередине оказались числа 17 и 19. Находим их среднее значение:
Число 18 и является медианой данного ряда чисел.
Среднее арифметическое, размах и мода — справочник студента
Пользуясь этим рядом, мы можем определить среднюю температуру воздуха, наблюдаемую в течение этих десяти дней.
средний балл ученика за четверть
среднюю урожайность пшеницы за последние 5 лет и так далее.
Вернёмся к нашему примеру. Обратите внимание, что температура воздуха в некоторые дни существенно отличается от 25 градусов Цельсия (то есть от средней температуры). Так, самая высокая температура равна 30 градусам, а самая низкая – 19 градусам.
Найдём разность между наибольшим и наименьшим значениями:
Размах ряда находят, когда хотят узнать, насколько велик разброс данных в ряду. Так, например, в нашем примере размах ряда показывает колебание температуры воздуха в течение 10 дней.
Но кроме среднего арифметического и размаха ряда данных, нас может заинтересовать вопрос: какая температура воздуха чаще всего устанавливалась за 10 дней? Заметим, что чаще всего в нашем ряду встречается число 25. Это число называют модой рассматриваемого ряда.
Также ряд может и не иметь моды.
Моду ряда находят, когда хотят выяснить некоторый характерный показатель. Например, удобно воспользоваться этим показателем при изучении спроса покупателей на мужскую обувь, чтобы определить какой размер самый популярный.
Рассмотрим ещё один пример.
Посмотрите, среднее арифметическое ряда чисел может не совпадать ни с одним из чисел ряда, а вот мода всегда совпадает хотя бы с одним из чисел. Причем, если среднее арифметическое мы можем найти только для числового ряда, то понятие «мода» относится не только к числовым рядам.
Например, проведя опрос группы людей, можно определить, какой из видов спорта более популярен. И модой будут служить те ответы, которые чаще всего встречаются.
Презентация «Среднее арифметическое, размах, мода, медиана — алгебра, презентации









Среднее арифметическое, размах, мода, медиана * Свяжите эти три картинки
Цель урока: сформировать представление о статистических закономерностях в реальном мире на примере размаха, моды, среднего арифметического, медианы. *
Вопрос 1. Округлите число 5,387 до сотых? * Ответы: А) 5,4 Б) 5,38 В) 5,3 Г) 5,39 Время на ответ 15 сек. Ваше время истекло Время
Среднее арифметическое ряда чисел Число месяца 1 2 3 4 5 6 7 8 9 10 Температура 3 5 5 7 6 4 6 9 10 15 В таблице записаны результаты ежедневного измерения в полдень температуры воздуха (в градусах Цельсия) в течение 10 дней: Средняя температура воздуха в полдень в первую декаду месяца: Т ср = 3 + 5 + 5 + 7 + 6 + 4 + 6 + 9 + 10 + 15 10 = 7 С о
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых. *
Найдите среднее арифметическое чисел 10 6 15 9 3
Группу из 12 семиклассников просили отметить в определенный день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: Сколько в среднем затратили учащиеся на выполнение домашнего задания по алгебре? * 23 18 25 20 25 25 32 37 34 26 34 25 27 минут
Вернемся к нашей задаче. Наибольший расход времени равен 37 минутам, а наименьший – 18 минутам. Разность между наибольшим и наименьшим расходом времени составляет … * 23 18 25 20 25 25 32 37 34 26 34 25 19 мин. Говорят, что размах ряда равен 19
Размах ряда чисел — колебание температуры воздуха в течение суток
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. *
нас могут заинтересовать не только среднее арифметическое и размах полученного ряда чисел, но и другие показатели. Например, какой расход времени является типичным для выделенной группы учащихся, т.е. какое число встречается в ряду данных чаще всего? * 25 мин. 25 – мода рассматриваемого ряда 23 18 25 20 25 25 32 37 34 26 34 25
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду. *
Мода ряда чисел Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду. 23 33 23 27 25 26 23 29 28 23 Мода: число 23 14, 18, 22, 26, 30, 28, 26, 24, 22, 20 Моды: числа 22 и 26 14, 18, 22, 26, 30, 32, 34, 36, 38, 40 Моды нет
Упорядоченный ряд чисел: 1, 2, 2, 3, 4, 4, 5, 5, 5 Среднее арифметическое: Размах: 5 – 1=4 Мода: 5 * Провести статистический анализ нашего опроса в начале урока по вариантам.
Работа по учебнику. № 171. Определить среднее, размах, моду и медиану. *
Медиана Номера квартир 1 2 3 4 5 6 7 8 9 Расход электроэнергии, кВтч 85 64 78 93 72 91 72 75 82 Расход электроэнергии жильцами 9 квартир: Упорядоченный ряд: 64, 72, 72, 75, 78, 82, 85, 91, 93 Медиана
Итог урока. Чему вы научились сегодня на уроке? Почему так важны статистические характеристики? Как найти среднее арифметическое, моду и размах ряда чисел? Эти знания пригодятся вам во время проведения различных социологических опросов в рамках различных проектов. *
Домашнее задание пункт 9 № 169, №172. *
Средние величины в статистике: сущность, свойства, виды. Примеры решения задач
Виды средних величин, используемых в статистике
Рассмотрим основные виды средних величин, используемых при решении социально-эконмических и аналитических задач.
Средняя арифметическая простая вычисляется по формуле:
 |
Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по не сгруппированным данным. Пример применения формулы средней арифметической простой представлен в задаче 1.
Средняя арифметическая взвешенная определяется по формуле:
 |
При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам. Пример применения формулы средней арифметической взвешенной представлен в задаче 2.
Средняя гармоническая простая определяется по формуле:
 |
Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для знаменателя ее необходимо предварительно определить.
Средняя гармоническая взвешенная определяется по формуле:
 |
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов. Пример применения формулы средней гармонической взвешенной представлен в задаче 3.
Средняя геометрическая простая (невзвешенная) опеределяется по формуле:
 |
Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
Средняя квадратическая простая (невзвешенная) опеределяется по формуле:
 |
Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей.
Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана.
Мода (Мо) представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Пример определения медианы и моды для дискретного ряда чисел представлен в задаче 1.
 |
Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Для интервального ряда расчет моды осуществляется по формуле:
 |
где Хо — нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i — величина модального интервала; f Мо — частота модального интервала; f Мо-1 — частота интервала, предшествующего модальному; f Мо+1 — частота интервала, следующего за модальным.
Для интервального ряда расчет медианы осуществляется по формуле:
 |
Хо — нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i — величина медианного интервала; Sme-1 — накопленная частота интервала, предшествующего медианному; f Me — частота медианного интервала.
Примеры решения задач по теме «Средние величины в статистике»
Задача 1. Дан ряд чисел: 15; 15; 12; 14; 13. Найдите размах, среднее арифметическое, медиану и моду этого ряда.
3) Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12; 13; 14; 15; 15. Медиана нечетного количества чисел в дискретном ряде – это число, записанное посередине. Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Поскольку в нашем случае количество чисел ряда нечетноне, то Ме = 14.
4) Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. Так как число 15 встречается в нашем ряде чаще других, то Мо = 15.
Задача 2. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе определим по формуле средней арифметической взвешенной: Хср = (15×15+3×10+7×20) / (15+3+7) = 15,8%.
Ответ. Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе равен 15,8%, число этих студентов – 3 950 человек.
Задача 3. Сумма невыплаченной своевременно задолженности по кредитам на 1 июля составила 92,4 млн. денежных единиц. По отдельным отраслям экономики она распределялась следующим образом:
Определить средний процент невыплаченной своевременно задолженности. Обоснуйте выбор формы средней.
Решение
Поскольку на различных предприятиях сумма задолженности по кредитам разная при разных удельных весах, то применим формулу средней гармонической взвешенной. Хср = ΣW / Σ(W/х) = (32+14+46,4)/(32/20+14/28+46,4/16) = 92,4/5 = 18,48 %.
Ответ. Средний процент невыплаченной своевременно задолженности равен 18,48%.
Список использованных источников
Презентация на тему: Среднее арифметическое. Размах. Мода

«Дорогу осилит идущий,а математику — мыслящий»
Описание слайда:
Тема урока: Среднее арифметическое. Размах. Мода.
Описание слайда:
Цели: Научить находить среднее значение величин.Познакомить учащихся с элементами статистики. Познакомить учащихся с новыми понятиями мода и размах.
Описание слайда:
Задачи: Отбирать и систематизировать информацию.Составлять на основе данных таблицы и использовать их для подсчета результатов различных статистических наблюдений.Находить среднее арифметическое, размах и моду.
Описание слайда:
План урока: Организационный момент.Устная работа.Изучение нового материала.Закрепление нового материала.Исследовательская работа.Домашнее задание.Подведение итогов урока.
Описание слайда:
Устная работа Ученик получил в течение четверти отметки по алгебре 5, 2, 4, 5, 5, 4, 4, 5, 5, 5. Какую четвертную отметку поставит ему учитель?
Описание слайда:
Правильный ответ (5+2+4+5+5+4+4+5+5+5) : 10 = 4,4≈ 4
Описание слайда:
Изучение нового материала Задача1.12 семиклассников затратили на выполнение домашнего задания по алгебре время (мин.), показанное в таблице:
Описание слайда:
Понятие среднего арифметического Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Описание слайда:
Подумай Ученик 7 класса следил за своими отметками и точно знает, что в этой четверти получил 5, 5, 4, 5, 4, 5, 4, 5, 5, 4, 5. Он знает, что его четвертная отметка так как число 5 встречается чаще, чем число 4.
Описание слайда:
Определение моды. Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Описание слайда:
Описание слайда:
Описание слайда:
Физкультминутка Встаньте. Закройте глаза, очень сильно зажмурьтесь, откройте глаза. (3 раза) Голову держите прямо, глаза подняли вверх, опустили вниз, посмотрели влево, посмотрели вправо (3 раза). Голову откиньте назад, опустите вперёд так, чтобы подбородок упёрся в грудь (3 раза). Поднимите руки вверх, вперед, в стороны, опустили (3 раза).
Описание слайда:
Известно, что на планете Меркурий средняя температура + 15 0 Можно предположить, что при таком статистическом показателе, возможна жизнь человека на этой планете.Но на самом деле температура на Меркурии колеблется от – 150 0 до + 350 0.Найдите разность между наибольшим и наименьшим значениями температур.
Описание слайда:
Описание слайда:
По данным таблицы вычислите размах.
Описание слайда:
Найдите среднее арифметическое, размах и моду. На соревнованиях по фигурному катанию выступление было оценено баллами, представленными в таблице. Для этого ряда найдите среднее арифметическое, размах и моду.
Описание слайда:
Описание слайда:
1. Найдите среднее арифметическое ряда чисел: 4, 7, 6, 1, 2, 8, 9, 11а) 11; б) 8; в) 50; г) 6.2. Найдите моду ряда чисел: 12, 13, 13, 15, 19, 13, 12, 14, 12, 14, 13.а) 14; б) 13; в) 19; г) 123. Найдите размах ряда чисел:293, 812, 90, 2, 373, 28, 28.
а) 810; б) 812; в) 2; г) 28.4 В течении четверти ученица получила следующие отметки по алгебре: 2, 2, 2, 3, 3, 4, 4, 4, 4, 5.
Какую статистическую характеристику ученица предпочла бы при выставлении четвертной отметки:а) среднее арифметическое; б) мода; в) размах.
Описание слайда:
Правильный ответ: Г2. Б3. А4. Б
Описание слайда:
Домашнее задание П.9, № 181, № 183( если нужны задания, то №174, 177)
Описание слайда:
Подведём итоги! С какими новыми понятиями мы познакомились?
Описание слайда:
Хочется надеяться, что сегодняшний урок разбудит у вас жажду новых познаний, ведь «великий океан истины по-прежнему расстилается перед вами не исследованным до конца».
Мода — сайт учителя математики
В этом учебном
году мы начали изучать два предмета: алгебру и геометрию. При изучении алгебры
что-то мне знакомо из курса 5,6 классов, что-то мы изучаем более основательно и
углубленно, многое узнаем нового.
Вот новое для меня при изучении алгебры – это
знакомство с некоторыми статистическими характеристиками: размах и мода. Со
средним арифметическим мы встречались уже ранее.
Еще интересным оказалось, что
эти характеристики применяются не только на уроках математики, но и в жизни, на
практике (в производстве, в сельском хозяйстве, в спорте и т.д.).
Когда мы в
классе на уроке решали задачи к этому пункту, то возникла идея составить самим
задачи и подготовить к ним презентации, то есть как бы начать создавать свой
задачник.
Каждый придумывает задачу, делает к ней презентацию, как бы каждый
работает над своим мини-проектом, а на
уроке все вместе решаем, обсуждаем. Если
допущены ошибки, то их исправляем.
А в
конце провести публичную защиту этих
мини-проектов.
В
ходе изучения раздела «Статистические
характеристики» мы познакомились с
такими понятиями: среднее арифметическое, размах, мода. Эти характеристики находят
применение в статистике.
Эта наука изучает численность отдельных групп
населения страны и ее регионов, производство и потребление разнообразных видов
продукции, перевозку грузов и пассажиров различными видами транспорта,
природные ресурсы и т.п.
“Статистика знает всё”, – утверждали Ильф и Петров в своем
знаменитом романе “Двенадцать стульев” и продолжали: “Известно, сколько какой
пищи съедает в год средний гражданин республики… Известно, сколько в стране
охотников, балерин, станков, велосипедов, памятников, маяков и швейных машинок…
Как много жизни, полной пыла, страстей и мысли, глядит на нас со статистических
таблиц. ” Это ироническое описание дает довольно точное представление о
статистике (от лат. status – состояние) – науке, изучающей, обрабатывающей и
анализирующей количественные данные о самых разнообразных массовых явлениях в
жизни.
В школьном курсе
алгебры мы рассматриваем понятия и методы описательной статистики, которая
занимается первичной обработкой информации и вычислением наиболее показательных
числовых характеристик. По словам английского статистика Р. Фишера: “Статистика
может быть охарактеризована как наука о сокращении и анализе материала, полученного
в наблюдениях”.
Всю совокупность числовых данных, полученных в выборке можно
(условно) заменить несколькими числовыми параметрами, некоторые из них мы уже
рассматривали на уроках – это среднее арифметическое, размах, мода.
Результаты
статистических исследований широко используются для практических и научных
выводов, поэтому важно уметь определять эти статистические характеристики.
Статистические характеристики в
наше время встречаются везде. Например,
перепись населения. Благодаря этой переписи, государство узнает сколько
нужно денег на строительство жилья, школ, больниц, сколько людей нуждаются в
жилье, сколько детей в семье, количество безработных, уровень зарплаты и т.д.
Результаты этой переписи сравнят с прошлой, посмотрят поднялась ли страна за
это время или положение стало хуже, можно будет сравнить данные с результатами
в других странах. В промышленности большое значение имеет мода. Например,
товар, который имеет большой спрос — будут всегда продавать, а фабрики будут
иметь большие деньги.
И таких примеров множество.
Результаты статистических исследований широко используются
для практических и научных выводов.[2]
Определение 1. Средним
арифметическим ряда чисел называется частное от деления суммы этих чисел на
число слагаемых.[3]
Пример: При изучении учебной нагрузки выделили группу из 12
учащихся 7 класса. Просили отметить в определенный день время (в минутах),
затраченное на выполнение домашнего задания по алгебре. Получили такие данные:
23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25. Имея этот ряд
данных, можно определить, сколько минут в среднем затратили учащиеся на
выполнение домашнего задания по алгебре. Для этого надо сложить указанные 12
чисел и полученную сумму разделить
Определение 2. Модой ряда чисел
называется число, которое встречается в данном ряду чаще других.[4]
Пример: При анализе сведений о времени, затраченном
учащимися на выполнение домашнего задания по алгебре, нас могут заинтересовать
не только среднее арифметическое и размах полученного ряда данных, но и другие
показатели.
Например, интересно знать, какой расход времени является
типичным для выделенной группы учащихся,
т.е. какое число встречается в ряду данных чаще всего. Нетрудно заметить, что в
нашем примере это число 25.
говорят, что число 25 – мода рассматриваемого ряда.
Ряд чисел может иметь более одной моды, а может не иметь
моды совсем. Например, в ряду чисел 47, 46, 50, 47, 52, 49, 45, 43, 54, 52, 47,
52 две моды – это числа 47 и 52, так как каждое из них встречается в ряду по
три раза, а остальные числа – менее трех раз.
В ряду чисел 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72
моды нет.
Моду
ряда данных обычно находят, когда хотят выявить некоторый типичный показатель. Мода—показатель, который широко используется в статистике.
Одним из наиболее частых использований моды является изучение спроса. Например,
при решении вопросов, в пачки какого веса фасовать масло, какие открывать
авиарейсы и т. п.
, предварительно изучается спрос и выявляется мода — наиболее
часто встречающийся заказ.
Однако нахождение среднего арифметического или моды далеко
не всегда позволяет делать надежные выводы на основе статистических данных.
если у нас есть ряд данных, то для обоснованных выводов и надежных прогнозов на
их основе, помимо средних значений, надо еще указать, насколько используемые
данные различаются между собой.
Одним из статистических показателей различия
или разброса данных является размах.
Определение 3. Размахом ряда чисел
называется разность между наибольшим и наименьшим из этих чисел.[5]
Пример: В рассмотренном выше примере мы нашли, что в
среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27
минут. Однако анализ проведенного ряда данных показывает, что время, затраченное
некоторыми учащимися, существенно отличается от 27 минут, т.е.
от среднего
арифметического. Наибольший расход равен 37 минут, а наименьший – 18 минут.
Разность между наибольшим и наименьшим расходом времени составляет 19 минут.
Вот в этом случае рассматривается еще одна статистическая характеристика –
размах.
Размах ряда находят, когда хотят
определить, как велик разброс данных в ряду.
А
теперь хочу представить результаты нашей работы: мини-проекты для создания
задачника по статистике.
Задача № 1. Автор Кушнарев Павел, учащийся 7 класса.
Я
работаю в салоне-магазине «Супер-авто» главным менеджером отдела продаж. Наш салон предоставлял автомобили для участия
в игре «полный привод». В прошлом году на
выставке-продаже наши машины имели успех! Результаты продаж следующие:
| Продано машин в первый день | Продано машин во второй день | Продано машин в третий день | Продано машин в четвертый день | Продано машин в пятый день |
| 100 | 100 | 150 | 200 | 250 |
Отделу продаж необходимо подвести
итоги выставки:
Ответ: в среднем было продано по
150 машин в день, разброс количества проданных машин составил – 150, в день
чаще всего продавалось 100 машин.
Задача № 2.
Автор Петрова Анастасия, ученица 7 класса.
Я, Анастасия Волочкова, была приглашена в жюри на финал конкурса «Лёд и
пламя». Конкурс проходил в городе Санкт –Петербурге. В финал вышли три пары самых сильных фигуристов: 1пара.
Жюри
выставили следующие оценки:
| Жюри | Баллы 1 пары | Баллы 2 пары | Баллы 3пары |
| Анастасия Волочкова | 5.5 | 5.4 | 5.4 |
| Елена Малышева | 5.5 | 5.2 | 5.3 |
| Алексей Далматов | 5.3 | 5.2 | 5 |
Найдите среднее арифметическое, размах моду в рядах оценок каждой пары.
| Итоги | Среднее арифметическое | Размах | Мода |
| 1 пара | 5.43 | 0.2 | 5.5 |
| 2 пара | 5.27 | 0.2 | 5.2 |
| 3 пара | 5.23 | 0.4 | нет |
Задача № 3.
Автор Селянская Юлия, ученица 7 класса.
В этом году я побывала в г.
Санкт-Петербург на соревнованиях по бальным танцам. В конкурсе принимали
участие три красивые пары: Сушенцова Елена и Хлебодаров Кирилл, Батуева Алина и
Слепнев Павел, Джаниашвили Виктория и Ткачев Валерий.
За выступления пары получили
следующие оценки:
Найти среднюю оценку, размах и
моду.
| Пары | Среднее арифметическое | Размах | Мода |
| №1 | 4,42 | 0,2 | 4,5 |
| №2 | 4,37 | 0,2 | 4,3 |
| №3 | 4,37 | 0,2 | 4,3 |
Задача № 4.
Автор Сушенцова Елена.
Я директор магазина модной одежды и аксессуаров «Fashion». Магазин приносит хорошую прибыль. Показатели продаж за прошлый год:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 915т.р. | 1млн 150т.р. | 1 млн. 980т.р. | 2 млн. 3т.р. | 2 млн. 950т.р. | 3 млн. 950т.р. | 3 млн. 100т.р. | 2 млн. 950т.р. | 3 млн. | 3 млн. 750т.р. | 2млн. 950т.р. | 4 млн. 250т.р. |
Первые 2-3 месяца прибыль доходила до 2 миллионов за месяц. Уже после
прибыль возрастала до 4 миллионов. Самыми удачными месяцами были: декабрь и
май. В мае в основном покупали платья для выпускных баллов, а в декабре для
новогоднего торжества.
Вопрос моему главному бухгалтеру: каковы результаты нашей работы за
год?
| Среднее арифметическое | 2 745 000 руб |
| Размах | 4 158 500 руб |
| Мода | 2 950 000 руб |
Задача №5.
Авторы Слепнев Павел и Афанасьев Дмитрий, учащиеся 7 класса.
В
заключении я хочу сказать, что мне нравится эта тема.
Статистические характеристики очень удобны, их можно применять везде. В общем,
они сравнивают, стремятся к прогрессу и помогают узнать мнение народа.
В
ходе работы над этой темой я
познакомился с наукой статистикой, узнал некоторые понятия (среднее арифметическое, размах и мода), где
эта наука может быть применима, расширил свои познания и в информатике.
Я,
думаю, что наши задачки как примеры для освоения этих понятий пригодятся и
другим! Будем продолжать знакомство в этой наукой и
создавать свои задачки!
Вот и
закончилось мое путешествие в мир
математики, информатики и статистики. Но
я, думаю, что не последнее. Я еще многое
хочу познать! Как сказал Галилео Галилей: «Природа формулирует свои законы
языком математики». И я хочу овладеть
этим языком!
1.
Бунимович Е.А., Булычев В.А. «Вероятность и статистика в курсе
математики общеобразовательной школы», М.: Педагогический университет “Первое
сентября”, 2005
2.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
«Алгебра, 7 класс», М: «Просвещение», 2009
3.
Макарычев Ю.Н., Миндюк Н.Г. «Алгебра.
Элементы статистики и теории вероятностей», 7 – 9 классы. – М.: Просвещение,
2005.
[1] Бунимович
Е.А., Булычев В.А. «Вероятность
и статистика в курсе математики общеобразовательной школы»
[2] Макарычев Ю.Н., Миндюк Н.Г. «Алгебра.
Элементы статистики и теории вероятностей»
Приемы статистики
Статистика собирает, обрабатывает и анализирует данные (числа, тексты и другие типы данных). Сейчас вы увидите, как знание основ статистики помогает в различных реальных задачах.
Зачастую в жизни приходится искать нечто среднее в наборе (или ряде) чисел. Допустим, вы хотите узнать, сколько в среднем потратили за каждый месяц в году. Или наоборот заработали, если у вас разный ежемесячный доход. Тогда вы просто ищите среднее арифметическое или просто среднее. Т.е. складываете все числа и делите на их количество:
Придадим другой смысл этим четырем числам и допустим, что это очки, заработанные любимой командой в четырех играх. И тогда нам уже важно, в какой игре они получили больше, а в какой меньше.
Зная наибольшее и наименьшее, мы можем посчитать размах чисел, вычитая из большего числа меньшее: 28 — 16 = 12 (размах равен 12). Например, здесь, размах результатов существенный, значит, игра ведется не очень стабильно, либо были выбраны слишком сильные соперники.
Можно искать не только среднее арифметическое, но и медиану, т.е. среднее число. Ведь если вы считаете зарплаты всех людей в стране, то средне арифметически они получаются довольно хорошие:
(15 + 18 + 25 + 28 + 36 + 47 + 160) / 7 = 329 / 7 = 47
Но это число несколько искажает реальность, показывая скорее средне-высокий уровень дохода.
Поэтому, если какие-то единичные величины сильно завышены, со среднее считать бесполезно. Здесь берется медиана (упорядоченного набора) — среднее число из упорядоченного ряда (в данном случае 28) и оно будет практически одинаково близко и к 47 и к 15, и значительно точнее охарактеризует реальную ситуацию.
Если же чисел в ряду четное количество, как было в нашем примере с победами в играх, то для расчета медианы берутся два средних числа и считается их среднее арифметическое: (23 + 25) / 2 = 24. Тут практически совпало с нашим средним арифметическим.
Иногда правильнее взять медиану (произвольного набора), когда мы все равно не имеем на руках всей статистики.
Допустим, мы только что подключили счетчик посещений на сайте и хотим понять, сколько времени у нас проводит средний посетитель. Для этого мы можем взять статистику хотя бы за неделю посещений и все эти числа принять за медиану.
Ведь, по сути, нам неизвестно, что было до этой недели или станет после, мы опираемся на срез настоящего.
Мода числа (или самое модное число) — это наиболее часто встречающееся в наборе число. Тоже возможно как вариант определения среднего. Если числа различны, то моды, конечно, нет. Но, допустим, с помощью моды, мы легко можем посмотреть, какие размеры одежды покупают у нас в магазине чаще всего, соответственно, заказывать этого товара больше.