Что такое размер измеряемой величины метрология
Метрология
Измеряемые величины, виды и области измерений
Основные метрологические понятия
Основными проблемами, которыми занимается метрология, являются:
Понятие о размере
Различают следующие основные понятия размера:
Истинным значением размера называется значение размера, свободное от погрешностей измерений. Истинное значение размера неизвестно и его нельзя определить, так как все средства измерений имеют погрешности, некоторые из которых нельзя учесть и компенсировать.
Погрешностью (ошибкой) измерения называется разность между полученным при измерении значением размера и его истинным значением. Так как истинное значение измеряемой величины неизвестно, то оно заменяется ее точным или действительным значением.
Погрешность прибора может быть также выражена в долях или процентах значения измеряемой величины. В этом случае она называется относительной погрешностью.
Меры и измерительные приборы всегда имеют погрешности, которые изменяются с течением времени в результате износа или старения измерительных средств. Поэтому меры и приборы должны периодически калиброваться.
Калибровкой (сличением) называется процесс определения действительного отклонений показаний прибора или инструмента от заданного значения и соответствия мер и измерительных приборов техническим требованиям.
Калибровка производится посредством образцовых измерительных приборов или мер. Результаты калибровки могут быть использованы для компенсации систематических погрешностей приборов и инструментов.
Калибровку производят изготовители приборов и инструментов, лаборатории, производственные предприятия. Компенсация систематических погрешностей широко применяется при калибровке электронных (индуктивных, инкрементных) измерительных приборов.
Измеряемые величины
Измерения физических величин подразделяются на следующие области и виды:
1. Измерения геометрических величин:
2. Измерения механических величин:
3. Измерения параметров потока, расхода, уровня, объема веществ:
4. Измерения давлений, вакуумные измерения:
5. Физико-химические измерения:
6. Теплофизические и температурные измерения:
7. Измерения времени и частоты:
8. Измерения электрических и магнитных величин на постоянном и переменном токе:
9. Радиоэлектронные измерения:
10. Измерения акустических величин:
11. Оптические и оптико-физические измерения:
12. Измерения ионизирующих излучений и ядерных констант:
Метрология
Размерности измеряемых величин, шкалы и отсчеты
Понятие о размерности измеряемых величин
При определении размерности производных величин руководствуются следующими правилами:
1. Размерности левой и правой частей уравнений не могут не совпадать, так как сравниваться между собой могут только одинаковые свойства. Объединяя левые и правые части уравнений, можно прийти к выводу, что алгебраически суммироваться могут только величины, имеющие одинаковые размерности.
Итак, всегда можно выразить размерность производной физической величины через размерности основных физических величин с помощью стеᴨенного одночлена:
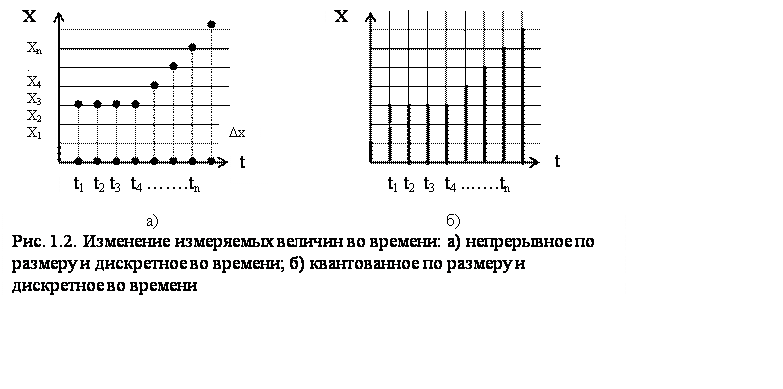
Размер измеряемой величины является количественной ее характеристикой. Получение информации о размере физической или нефизической величины является содержанием любого измерения.
Измерительные шкалы и их типы
В теории измерений принято, в основном, различать пять типов шкал: наименований, порядка, разностей (интервалов), отношений и абсолютные.
Шкалы разностей (интервалов) отличаются от шкал порядка тем, что по шкале интервалов можно уже судить не только о том, что размер больше другого, но и на сколько больше. По шкале интервалов возможны такие математические действия, как сложение и вычитание.
Характерным примером является шкала интервалов времени, поскольку интервалы времени можно суммировать или вычитать, но складывать, например, даты каких-либо событий не имеет смысла.
Шкалы отношений описывают свойства, к множеству самих количественных проявлений котоҏыҳ применимы отношения эквивалентности, порядка и суммирования, а следовательно, вычитания и умножения. В шкале отношений существует нулевое значение показателя свойства. Примером является шкала длин.
Любое измерение по шкале отношений заключается в сравнении неизвестного размера с известным и выражении первого через второй в кратном или дольном отношении.
Измерение (сравнение неизвестного с известным) происходит под влиянием множества случайных и неслучайных, аддитивных (прибавляемых) и мультипликативных (умножаемых) факторов, точный учёт которых невозможен, а результат совместного воздействия непредсказуем.
Из приведенной формулы можно выразить значение измеряемой величины Q :
При однократном измерении величины ее значение подсчитывается с учетом поправки:
Значение измеряемой величины при многократном измерении может быть определено из соотношения:
Бирюков С., Чередов А. Метрология: Тексты лекций
ОГЛАВЛЕНИЕ
1. МЕТРОЛОГИЯ. ОСНОВНЫЕ ПОНЯТИЯ В ОБЛАСТИ МЕТРОЛОГИИ
Метрология является одной из областей науки и её роль за последние десятилетия чрезвычайно возросла. Метрология проникла и завоевала (или завоевывает) себе позиции во всех областях жизни и деятельности человечества. В силу этого обстоятельства метрологическая терминология тесно соприкасается с терминологией каждой из «специальных сфер».
В нашей стране действует стандарт на терминологию ГОСТ 16263—70 «Государственная система обеспечения единства измерений. Метрология. Термины и определения» и закон об обеспечении единства измерений*, вводящий новые понятия и определения и уточняющий ранее действующие.
Далее в разделе рассматриваются некоторые основные понятия и относящиеся к ним термины и определения, нашедшие широкое применение и выходящее за рамки метрологии. Поэтому их рассмотрение нельзя отнести к какому-либо разделу метрологии. С другой стороны, многие из этих терминов именно в силу их широкого распространения получают искаженное толкование, неправильно применяются или заменяются неправильными терминами. Не установив единства понимания и толкования таких общих терминов, практически невозможно излагать ни одного раздела метрологии.
В некоторых случаях, когда нельзя непосредственно сравнить измеряемую величину с воспроизводимой единицей физической величины, используют измерительное преобразование. Это такой вид преобразования, при котором устанавливается однозначное соответствие между значениями двух величин (входной и выходной). Зависимость между этими величинами стремятся сделать линейной. Диапазон преобразования определяется множеством значений входной величины, подвергаемой преобразованию [1].
1.12. Точность измерений
Термин «точность измерения» применяется очень широко, однако пока нет общепринятого способа выражать точность измерения количественно. В ГОСТ 16263—70 сказано: «Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Например, если погрешность измерений равна 10-2 % = 10-4, то точность равна 104. Такой способ количественного выражения точности был предложен давно, однако он широко не распространился.
Под точностью измерения понимают степень приближения результатов измерений к истинному значению измеряемой величины. Однако выражения вроде «точность измерения равна 0,1 %» или «результат измерения верен с точностью до 0,001» неправильны. Термин же «точность» применим лишь для сравнения результатов или относительной характеристики методов измерений, например, точность измерения длины с помощью микрометра больше, чем при измерении с помощью штангенциркуля [4].
Поверка средств измерений
Классификация и основные характеристики измерений
Классификация измерений:
1. По признаку точности — равноточные и неравноточные измерения.
Равноточные измерения— определенное количество измерений любой величины, произведенных аналогичными по точности средствами измерений в одинаковых условиях.
Неравноточные измерения— определенное количество измерений любой величины, произведенных отличными по точности средствами измерений и (или) в различных условиях.
Методы обработки равноточных и неравноточных измерений несколько отличаются. Поэтому перед тем как начать обработку ряда измерений, обязательно нужно проверить, равноточные измерения или нет.
Это осуществляется с помощью статистической процедуры проверки по критерию согласия Фишера.
2. По числу измерений — однократные и многократные измерения.
Однократное измерение— измерение, произведенное один раз.
Многократное измерение— измерение одного размера величины, результат этого измерения получают из нескольких последующих однократных измерений (отсчетов).
Во многих случаях, особенно в быту, производятся чаще всего однократные измерения. Как пример, измерение времени по часам как правило делают однократно. Однако при некоторых измерениях для убеждения в правильности результата однократного измерения может быть недостаточно. Поэтому часто и в быту рекомендуется проводить не одно, а несколько измерений. Например, ввиду нестабильности артериального давления человека при его контроле целесообразно проводить два или три измерения и за результат принимать их медиану. От многократных измерений двукратные и трехкратные измерения отличаются тем, что их точность не имеет смысла оценивать статистическими методами.
3. По характеру изменения измеряемой величины — статические и динамические измерения.
Динамическое измерение— измерение величины, размер которой изменяется с течением времени. Быстрое изменение размера измеряемой величины требует ее измерения с точнейшим определением момента времени. Например, измерение расстояния до уровня поверхности Земли с воздушного шара или измерение постоянного напряжения электрического тока. По существу динамическое измерение является измерением функциональной зависимости измеряемой величины от времени.
Статическое измерение— измерение величины, которая принимается в соответствии с поставленной измерительной задачей за неизменяющуюся на протяжении периода измерения. Например, измерение линейного размера изготовленного изделия при нормальной температуре можно считать статическим, поскольку колебания температуры в цехе на уровне десятых долей градуса вносят погрешность измерений не более 10 мкм/м, несущественную по сравнению с погрешностью изготовления детали. Поэтому в этой измерительной задаче можно считать измеряемую величину неизменной. При калибровке штриховой меры длины на государственном первичном эталоне термостатирование обеспечивает стабильность поддержания температуры на уровне 0,005 °С. Такие колебания температуры обусловливают в тысячу раз меньшую погрешность измерений — не более 0,01 мкм/м. Но в данной измерительной задаче она является существенной, и учет изменений температуры в процессе измерений становится условием обеспечения требуемой точности измерений. Поэтому эти измерения следует проводить по методике динамических измерений.
4. По цели измерения — технические и метрологические измерения.
Технические измерения— измерения с целью получения информациио свойствах материальных объектов, процессов и явлений окружающего мира.
Их производят, как пример, для контроля и управления экспериментальными разработками, контроля технологических параметров продукции или всевозможных производственных процессов, управления транспортными потоками, в медицине при постановке диагноза и лечении, контроля состояния экологии и др.
Технические измерения проводят, как правило, при помощи рабочих средств измерений. Однако нередко к проведению особо точных и ответственных уникальных измерительных экспериментов привлекают эталоны.
Метрологические измерения— измерения для реализации единства и необходимой точности технических измерений.
• воспроизведение единиц и шкал физических величин первичными эталонами и передачу их размеров менее точным эталонам;
• калибровку средств измерений;
• измерения, производимые при калибровке или поверке средств измерений;
• другие измерения, выполняемые с этой целью (например, измерения при взаимных сличениях эталонов одинакового уровня точности) или удовлетворения других внутренних потребностей метрологии (например, измерения с целью уточнения фундаментальных физических констант и справочных стандартных сведений о свойствах материалов и веществ, измерения для подтверждения заявленных измерительных возможностей лабораторий).
Метрологические измерения проводят при помощи эталонов.
Очевидно, что продукция, предназначенная для потребления (промышленностью, сельским хозяйством, армией, государственными органами управления, населением и др.) создается с участием технических измерений. А система метрологических измерений — это инфраструктура системы технических измерений, необходимая для того, чтобы последняя могла существовать, развиваться и совершенствоваться.
5. По используемым размерам единиц — абсолютные и относительные измерения.
Относительное измерение— измерение отношения величины к одноименной величине, занимающее место единицы. Например, относительным измерением является определение активности радионуклида в источнике методом измерения ее отношения к активности радионуклида в ином источнике, аттестованном как эталонная мера величины.
Противоположным понятием является абсолютное измерение.
При проведении этого измерения в распоряжении экспериментатора не имеется единицы измеряемой величины. По этому приходится ее воспроизводить непосредственно в процессе измерений.
Это возможно двумя способами:
• получать «непосредственно из природного мира», т.е. воспроизводить его на основе использования физических законов и фундаментальных физических констант (такое измерение в международном словаре метрологических терминов VIM [11] называется фундаментальным измерением);
• воспроизводить единицу на основании известной зависимости между нею и единицами других величин.
И связи с этим можно определить абсолютное измерение следующим образом:
Как пример, измерение силы с помощью динамометра будет относительным измерением, а ее измерение путем использования физической константы g (ускорение всемирного тяготения) и мер массы (основной величины SI) — абсолютным.
Внедрение и метрологическое обеспечение относительных измерений, как правило, являются наилучшим решением многих измерительных задач, поскольку они являются более простыми, точными и надежными, чем абсолютные измерения.
Абсолютные измерения в том смысле, которому больше соответствует понятие «фундаментальное измерение», на практике должны применяться в виде исключения. Их сфера применения — независимое воспроизведение основных единиц SI и открытие новых физических закономерностей.
6. По способу получения результата измерений — совокупные, совместные, косвенные и прямые измерения.
Прямое измерение— это измерение, проведенное при помощи средства измерений, хранящего единицу или шкалу измеряемой величины. Как пример, измерение длины изделия штангенциркулем, электрического напряжения вольтметром и т.п.
Косвенное измерение— измерение, когда значение величины определяют на основании результатов прямых величин, функционально связанных с искомой.
Совокупные измерения — когда проводят измерения одновременно нескольких однородных величин, когда значения этих величин находят путем решения системы уравнений, получаемых при измерениях различных сочетаний этих величин.
Классический пример совокупных измерений — калибровка набора гирь по одной эталонной гире, проводимая путем измерений различных сочетаний гирь этого набора,и решения полученных уравнений.
Совместные измерения — проводимые одновременно измерения двух или нескольких разнородных величин для определения зависимости между ними.
Другими словами, совместные измерения — это измерения зависимостей между величинами.
Примером совместных измерений является измерение температурного коэффициента линейного расширения (ТКЛР). Оно проводится путем одновременных измерений изменения температуры образца испытываемого материала и соответствующего приращения его длины и последующей математической обработки полученных результатов измерений.
Следует также различать область, вид и подвид измерений.
Под областью измерений понимают совокупность измерений физических величин, свойственных какой-то области техники или науки и имеющих свою специфику.
В настоящее время выделяют следующие области измерений:
• измерения пространственно-временных величин;
• механические измерения (в том числе измерения кинематических и динамических величин, механических свойств материалов и веществ, механических свойств и форм поверхностей);
• измерения теплоты (термометрия, измерения тепловой энергии, теплофизических свойств веществ и материалов);
• электрические и магнитные измерения (измерения электрических и магнитных полей, параметров электрических цепей, характеристик электромагнитных волн, электрических и магнитных свойств веществ и материалов);
• аналитические (физико-химические) измерения;
• оптические измерения (измерения величин физической оптики, когерентной и нелинейной оптики, оптических свойств веществ и материалов);
• акустические измерения (измерения величин физической акустики и акустических свойств веществ и материалов);
• измерения в атомной и ядерной физике (измерения ионизирующих излучений и радиоактивности, а также свойств атомов и молекул).
Вид измерений — это часть области измерений, которая имеет свои специфические особенности и которая отличается однородностью измеряемых величин.
Например, в области магнитных и электрических измерений возможно выделить измерения электрического сопротивления, электрического напряжения, ЭДС, магнитной индукции и т.д.
Подвид измерений — это часть вида измерений, которая выделяется спецификой измерений однородной величины (по диапазону, размеру величин, условиям измерений и др.).
Например, в измерениях длины выделяют измерения как больших длин (десятки, сотни и тысячи километров), так и малых и сверхмалых длин.
Что такое размер измеряемой величины метрология
РЕКОМЕНДАЦИИ ПО МЕЖГОСУДАРСТВЕННОЙ СТАНДАРТИЗАЦИИ
Государственная система обеспечения единства измерений
Основные термины и определения
State system for ensuring the uniformity of measurements. Metrology. Basic terms and definitions
Дата введения 2015-01-01
Цели, основные принципы и основной порядок проведения работ межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2009 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, применения, обновления и отмены»
Сведения о рекомендациях
1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологии им.Д.И.Менделеева» (ФГУП «ВНИИМ им.Д.И.Менделеева»)
2 ВНЕСЕНЫ Федеральным агентством по техническому регулированию и метрологии (Росстандарт)
3 ПРИНЯТЫ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 14 ноября 2013 г. N 44)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97
Сокращенное наименование национального органа по стандартизации
Минэкономики Республики Армения
Госстандарт Республики Беларусь
4 Приказом Федерального агентства по техническому регулированию и метрологии от 5 декабря 2013 г. N 2166-ст рекомендации по межгосударственной стандартизации РМГ 29-2013 введены в действие в Российской Федерации для применения в качестве рекомендаций по метрологии Российской Федерации с 1 января 2015 г.
Введение
За полтора десятка лет, прошедших с подготовки последней редакции РМГ 29, продолжалось развитие понятийного аппарата современной метрологии, отражающее расширение влияния метрологии на новые области измерений и отвечающее процессам глобализации и интеграции, происходящим в мировой экономике.
Современное представление основных понятий зафиксировано в последней редакции Международного словаря по метрологии (VIM3-2008)*, где основные изменения коснулись расширения таких понятий, как «метрология», «величина», а также включения ряда новых понятий, связанных с метрологической прослеживаемостью и неопределенностью измерений. Одной из задач актуализации РМГ 29 является гармонизация с международной терминологией, что направлено на обеспечение единого подхода к оценке качества результатов измерений, установление их метрологической прослеживаемости и, в конечном итоге, способствует взаимному признанию результатов измерений, калибровок, испытаний и выполнению международных обязательств стран СНГ.
Настоящие рекомендации содержат основные термины, используемые в метрологии. Часть терминов предыдущей редакции РМГ 29 исключены. Это касается, в первую очередь, ряда терминов, содержащихся в других межгосударственных документах и терминов, относящихся к организации деятельности метрологической службы.
Взаимные отношения между терминами иллюструет приложение А, содержащее схемы связи понятий.
1 Область применения
Настоящие рекомендации устанавливают основные термины и определения понятий в области метрологии.
Термины, установленные настоящим документом, рекомендуется применять во всех видах документации, научно-технической, учебной и справочной литературе по метрологии, входящих в сферу работ по стандартизации и (или) использующих результаты этих работ.
2 Метрология и ее разделы
2.1 метрология: Наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
2.2 теоретическая метрология: Раздел метрологии, предметом которого является разработка фундаментальных основ метрологии.
2.3 законодательная метрология: Раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц величин, эталонов, методов и средств измерений, направленных на обеспечение единства и требуемой точности измерений.
2.4 практическая (прикладная) метрология: Раздел метрологии, предметом которого являются вопросы практического применения разработок теоретической метрологии и положений законодательной метрологии.
practical (applied) metrology
3 Величины и единицы
3.1 величина: Свойство материального объекта или явления, общее в качественном отношении для многих объектов или явлений, но в количественном отношении индивидуальное для каждого из них.
3.2 размер величины: Количественная определенность величины, присущая конкретному материальному объекту или явлению.
3.3 род (величины): Качественная определенность величины.
kind of quantity, kind
3.4 значение величины: Выражение размера величины в виде некоторого числа принятых единиц, или чисел, баллов по соответствующей шкале измерений.
quantity value, value of a quantity, value
3.5 числовое значение (величины): Отвлеченное число, входящее в значение величины.
numerical quantity value, numerical value of a quantity, numerical value
3.6 система величин: Согласованная совокупность величин и уравнений связи между ними, образованная в соответствии с принятыми принципами, когда одни величины условно принимают за независимые, а другие определяют как функции независимых величин.
1 Порядковые величины, такие как твердость, измеряемая по шкале С Роквелла, обычно не рассматриваются как относящиеся к системе величин, так как они связаны с другими величинами только через эмпирические соотношения.
system of quantities
3.7 уравнение связи (между величинами): Математическое соотношение между величинами в данной системе величин, основанное на законах природы и не зависящее от единиц измерения.
3.8 основная величина: Одна из величин подмножества, условно выбранного для данной системы величин так, что никакая из величин этого подмножества не может выражаться через другие величины.
1 Подмножество, упоминаемое в этом определении, называется набором основных величин.
2 Основные величины относят к взаимно независимым, так как основная величина не может быть выражена как произведение степеней других основных величин.
3.9 производная величина: Величина, входящая в систему величин и определяемая через основные величины этой системы.
3.10 Международная система величин: Система величин, основанная на подмножестве семи основных величин: длины, массы, времени, электрического тока, термодинамической температуры, количества вещества и силы света.
International System of Quantities, ISQ
3.11 размерность (величины): Выражение в форме степенного одночлена, составленного из произведений символов основных величин в различных степенях и отражающее связь данной величины с величинами, принятыми в данной системе величин за основные с коэффициентом пропорциональности, равным 1.
1 Степени символов основных величин, входящих в одночлен, в зависимости от связи рассматриваемой величины с основными, могут быть целыми, дробными, положительными и отрицательными. Понятие размерности распространяется и на основные величины. Размерность основной величины в отношении самой себя равна единице, т.е. формула размерности основной величины совпадает с ее символом.
2 Символы, представляющие размерности основных величин в Международной системе величин, приведены в таблице 1.
quantity dimension, dimension of a quantity, dimension