Что такое разность квадратов

Как использовать разность квадратов a 2 − b 2

В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: вынесение общего множителя за скобки и способ группировки.

В этом уроке мы рассмотрим еще один способ разложения многочлена на множители с применением формул сокращённого умножения.

Прежде чем перейти к этому уроку обязательно выучите наизусть все формулы сокращенного умножения.

Рекомендуем каждую формулу прописать не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращённого умножения себе на небольшую шпаргалку.

Вспомним, как выглядит формула разности квадратов.

a 2 − b 2 = (a − b)(a + b)

(a − b)(a + b) = a 2 − b 2

Как разложить на множители разность квадратов

Рассмотрим пример. Необходимо разложить на множители разность квадратов.

Обратим внимание, что « 64y 2 » — это « (8y) 2 », значит, для формулы разности квадратов вместо « a » мы используем « 8y ».

Используем формулу разности квадратов. На месте « a 2 » у нас будет « 64y 2 », а на месте « b 2 » стоит « 36x 2 ».

Разность квадратов в обратную сторону

Рассмотрим другой пример. Требуется преобразовать произведение многочленов обратно в разность квадратов, используя формулу сокращенного умножения.

Обратим внимание, что произведение многочленов « (с + 3d)(с − 3d) » напоминает правую часть формулы разности квадратов « a 2 − b 2 = (a − b)(a + b) », только вместо « a » стоит « c », а на месте « b » стоит « 3d ».

Используем для « (с + 3d)(с − 3d) » формулу разности квадратов в обратную сторону.

Рассмотрим другой пример. Требуется упростить произведение многочленов.

Одночлены, которые стоят на месте « a » или « b » как в формуле, могут стоять в степени.

Например, в рассматриваемом примере на месте « a » стоит « x 2 ». Это означает, что именно « x 2 » мы рассматриваем как « a ».

Используем формулу разности квадратов и решим пример до конца.

Рассмотрим пример сложнее. Требуется разложить на множители многочлен, используя формулу разности квадратов.

Представим « (a + 2b) 2 − 9a 2 » как разность квадратов « a 2 − b 2 ».

Одночлены, которые стоят на месте « a » или « b » как в формуле, могут быть в скобках, т.е. быть многочленами.

В рассматриваемом примере на месте « a 2 » стоит многочлен « (a + 2b) 2 ». Это означает, что мы рассматриваем всю скобку « (a + 2b) » как « a » для формулы.

Решим пример до конца. После применения формулы разности квадратов не забудем привести подобные в примере.

Источник

Разность квадратов: формулы

Что такое разность квадратов

Разность квадратов двух чисел или выражений равняется сумме этих чисел/выражений, умноженной на их разность. То есть формула представляет собой разложение многочлена на множители:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Доказательство формулы разности квадратов

Арифметическое доказательство

Чтобы подтвердить справедливость определения разности квадратов, рассмотрим правую часть уравнения.

Раскроем скобки и получим:

(a+b)(a−b)=a 2 +ab−ba−b 2 =a 2 −b 2

Справедливость формулы доказана.

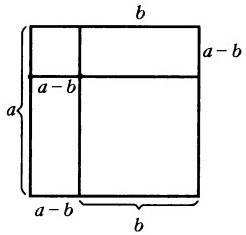
Геометрическое доказательство

Продолжим любую прямую, на которой лежит сторона меньшего квадрата, до пересечения со стороной большего четырехугольника. В результате внутри исходного квадрата со стороной a имеем:

Теперь найдем величину, которая останется при вычитание площади меньшего квадрата из площади большего. Как видим по чертежу, она равна площадям двух образовавшихся прямоугольников, то есть:

Применение формулы разности квадратов

Формула разности квадратов в алгебре может использоваться в двух видах случаев:

Примеры прямого использования формулы и формулировка стандартной ошибки

Необходимо раскрыть скобки в выражении: \(\left(15m-12n\right)\left(15m+12n\right)\)

Исходя из формулы, запишем:

Подставим в полученное выражение исходные переменные:

Стандартная ошибка прямого использования формулы заключается в следующем. Если в исходном выражении переместить в начало множитель со знаком плюс, при этом поменяв местами слагаемые, то получим:

В данном варианте записи зачастую происходит путаница с уменьшаемым и вычитаемым, то есть:

Следует обратить внимание на множитель со знаком минус.

Раскройте скобки: \(\left(4e+8f\right)\left(8f-4e\right)\)

Учитывая возможность совершения стандартной ошибки при использовании формулы сокращенного умножения (разности квадратов), обращаем внимание на второй множитель, выраженный разностью. Чтобы применить формулу, нам необходимо поменять местами слагаемые в первом множителе. Тогда получим:

Выполним подстановку исходных переменных:

Видим, что числитель раскладывается на множители по формуле разности квадратов:

Источник

Формулы сокращённого умножения

При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.

Следует также помнить, что вместо « a » и « b » в формулах могут стоять как числа, так и любые другие алгебраические многочлены.

Разность квадратов

Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

a 2 − b 2 = (a − b)(a + b)

Квадрат суммы

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.

(a + b) 2 = a 2 + 2ab + b 2

Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:

Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.

Предостережение!

Квадрат разности

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

(a − b) 2 = a 2 − 2ab + b 2

Также стоит запомнить весьма полезное преобразование:

Формула выше доказывается простым раскрытием скобок:

(a − b) 2 = a 2 −2ab + b 2 = b 2 − 2ab + a 2 = (b − a) 2

Куб суммы

Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Как запомнить куб суммы

Запомнить эту «страшную» на вид формулу довольно просто.

Предостережение!

Куб разности

Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a − b) 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Запоминается эта формула как и предыдущая, но только с учётом чередования знаков « + » и « − ». Перед первым членом « a 3 » стоит « + » (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять « − », затем опять « + » и т.д.

(a − b) 3 = + a 3 − 3a 2 b + 3ab 2 − b 3 = a 3 − 3a 2 b + 3ab 2 − b 3

Сумма кубов

Не путать с кубом суммы!

Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a 3 + b 3 = (a + b)(a 2 − ab + b 2 )

Сумма кубов — это произведение двух скобок.

Разность кубов

Не путать с кубом разности!

Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

a 3 − b 3 = (a − b)(a 2 + ab + b 2 )

Будьте внимательны при записи знаков.

Применение формул сокращенного умножения

Следует помнить, что все формулы, приведённые выше, используется также и справа налево.

Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.

Таблицу со всеми формулами сокращённого умножения вы можете скачать в разделе «Шпаргалки».

Источник

Алгебра

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Разность квадратов

Пусть есть два числа, одно из которых равно a, а другое – b. Их сумма будет равна a + b, а разность составляет a– b. Оба эти выражения являются многочленами.

Теперь перемножим сумму и разность, пользуясь правилами перемножения многочленов (см. урок 6) :

Слагаемые – a b и b a являются подобными, их сумма равна нулю:

Поэтому в выражении их можно сократить:

Получается, что произведение суммы двух чисел на их разность равно разности их квадратов. Естественно, как и любое другое математическое равенство, это можно переписать в обратном порядке:

Данное тождество называют формулой разности квадратов.

Вместо a и b в это тождество можно подставлять любые числа, выражения, одночлены, многочлены. Убедимся в ее справедливости на нескольких примерах. Вычислим значение выражения

сначала напрямую, а потом с помощью формулы разности квадратов:

Видно, что ответ не зависит от способа вычисления. Однако в ряде один из них представляется более удобным.

Решение. Возводить во вторую степень четырехзначные числа без калькулятора тяжело, поэтому используем сокращенное умножение:

Пример. Вычислите 499•501.

Решение. Используем две простые замены:

С их помощью вычисления существенно упрощаются, так как произведение можно представить как разность квадратов двух чисел:

Пример. Докажите, что число 765873 2 – 765864 2 делится на 9.

Решение. Разность квадратов равна:

Даже не складывая слагаемые во второй скобке, мы можем сказать, что исходное число делится на 9, так как на 9 делится один из множителей, на которые мы разложили разность квадратов.

Теперь рассмотрим случаи, когда в формулу подставляются переменные. Пусть необходимо найти произведение полиномов 8u + 5v и 8u– 5v. С помощью формулы сокращенного умножения получаем:

Конечно, мы могли бы выполнить эту операцию и без использования сокращенного умножения, просто раскрыв скобки методом «фонтанчика». Но тогда мы потратили бы больше времени, усилий и бумаги:

Пример. Упростите выражение

Иногда с помощью сокращенного умножения можно разложить полином на множители. Например, двучлен x 2 – 25 можно представить как

С помощью разложения разности квадратов на множители можно доказать, что разность вторых степеней двух последовательных натуральных чисел всегда является нечетным числом. Обозначим за n произвольное натуральное число. Тогда следующим за ним будет число n+1. Разность их квадратов равна

Число 2n +1 при делении на 2 дает остаток 1, то есть является нечетным.

Стоит отметить, что для суммы квадратов a 2 + b 2 аналогичной формулы разложения на множители не существует.

Квадрат суммы

Возведем во вторую степень сумму двух произвольных величин, которые обозначим буквами a и b:

(a + b) 2 = (a + b)(a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2

То есть верно тождество

(a + b) 2 = a 2 + 2ab + b 2

Это тождество называют формулой квадрата суммы.

Покажем ее верность на числовом примере. Вычислим значение выражения (5 + 3) 2 двумя различными способами, с помощью формулы возведения суммы в квадрат и без нее:

(5 + 3) 2 = 5 2 + 2 * 5 * 3 + 3 2 = 25 + 30 + 9 = 64

Выражение для квадрата суммы используется также, как и формула разности квадратов. В нее можно подставлять числа, полиномы и мономы, произвольные выражения. Тождество можно перевернуть, и тогда получится равенство:

a 2 + 2ab + b 2 = (a + b) 2

которое является верным.

Тождество можно проиллюстрировать и геометрически. Построим квадрат со стороной a + b (отрезки длиной а выделены красным цветом, а длиной b– синим):

Площадь такой фигуры равна второй степени стороны:

С другой стороны, этот квадрат составлен из двух прямоугольников площадью ab и квадратов со сторонами a и b:

Решение. Представим число 1010 как сумму 1000 и 10. Тогда можно записать:

(1010) 2 = (1000 + 10) 2 = 1000 2 + 2 * 1000 * 10 + 10 2 = 1000000 + 20000 + 100 = 1020100

Пример. Докажите, что число 9060100 является второй степенью натурального числа.

Решение. Представим 9060100 как сумму слагаемых 9000000, 60000 и 100. В свою очередь верны следующие равенства:

2 * 10 * 3000 = 60000

Тогда можно воспользоваться сокращенным умножением:

9060100 = 9000000 + 60000 + 100 = 3000 2 + 2 * 10 * 3000 + 10 2 = (3000 + 10) 2 = 3010 2

Получили, что 9060100 – это вторая степень числа 3010. При этом нам не пришлось извлекать квадратный корень.

В тождество квадрата суммы можно подставлять не только числа, но и многочлены. Представим в виде произведения мономов выражение

Сначала по формуле квадрата суммы раскроем каждую из скобок:

Далее приведем подобные слагаемые:

оставшийся полином раскладывается на множители с помощью сокращенного умножения:

Квадрат разности

Своя формула сокращенного умножения существует не только для квадрата суммы, но и для квадрата разности. Выведем её. Для этого возведем во вторую степень выражение a– b:

Итак, мы получили тождество, называемое формулой квадрата разности:

Убедимся в верности тождества на примере. Для этого вычислим значение выражения (9 – 5) 2 двумя разными способами, с использованием формулы возведения разности в квадрат и без неё:

Заметим, что если поменять местами переменные aи b, то значение квадрата их разности не изменится:

Дело в том, что числа a– b и b – a являются противоположными. В предыдущем уроке «Разложение многочленов на множители» мы узнали, что

Вторые же степени (как и вообще любые четные степени) противоположных чисел равны друг другу:

(-a) 2 = (-a)(-a) = (-1)*(-1)a 2 = a 2

Можно заметить сходство между тождествами для вычисления квадрата разности и суммы. Действительно, они отличаются лишь одним знаком. Поэтому иногда эти два тождества записывают как единое целое:

Если в левой скобке стоит плюс, то и в правой должен быть именно он. Если в левой части тождества стоит минус, то справа также должен стоять минус.

Решение. Перемножать два шестизначных числа весьма сложно. Однако заметим, что число 999999 можно представить как разницу миллиона и единицы:

Используем сокращенное умножение:

Несложно выполнить оставшиеся вычисления в столбик

Пример. Раскройте скобки в выражении (4m– 3) 2

Решение. Воспользуемся формулой сокращенного умножения:

Важно понимать, что вместо букв a и b могут стоять не только одночлены, но и полиномы. Пусть нам надо возвести во вторую степень полином

Если просто выполнить умножение методом «фонтанчика», то после раскрытия скобок получим 3•3 = 9 одночленов (так как исходный многочлен состоит из 3 мономов). Для упрощения представим исходный трехчлен как разность:

Тогда вторую степень можно найти так:

Пример. Докажите, что квадратный трехчлен m 2 – 16m + 66 ни при каких значениях переменной m не принимает отрицательные значения.

Известно, что вторая степень любого числа неотрицательна. Выделим в исходном трехчлене квадрат, содержащий переменную m. Для этого разложим число 66 как сумму 2 + 64:

При любом значении m выражение (m – 8) 2 неотрицательно, а значит, неотрицательно и значение (m – 8) 2 + 2. Более того, можно указать, что минимальное значение, которое может принимать исходный трехчлен, равно 2.

Заметим, что использованный в данном методе прием позволяет представить, по сути, любой квадратный трехчлен как разницу или сумму полного квадрата какого-то полинома и числа, что в свою очередь помогает оценить его максимальное или минимальное значение. Например, дан трехчлен 4v 2 + 12v – 10.Первое его слагаемое можно представить как квадрат какого-то числа:

Подобное действие в отношении трехчлена можно предпринять всегда, правда, иногда придется использовать квадратные корни, которые мы ещё не изучали детально. Далее второе слагаемое можно разложить на три множителя, одним из которых будет двойка, а вторым – тот самый одночлен, дающий при возведении во вторую степень первое слагаемое. Третий же множитель окажется каким-то числом:

Так как выражение (2v + 3) 2 не может быть меньше нуля, то и минимальное значение трехчлена 4v 2 + 12v– 10 равно(– 19)

Пример. Оцените возможные значения трехчлена – 9с 2 + 15с + 8

Воспользуемся таким же методом, но сначала вынесем знак минус за скобки, чтобы можно слагаемое 9c 2 представить как квадрат какого-то монома:

Значение выражения – (3с – 2,5) 2 может быть только меньше или равным нулю. Значит, исходный трехчлен не может принимать значения, большие, чем 14,25.

Формулы для кубов

До этого мы познакомились с тождествами, в которых величины возводились во вторую степень. Их будет достаточно почти для всех школьных заданий, в том числе и на ЕГЭ, поэтому необходимо сосредоточиться именно на их изучении.Однако в алгебре есть и более сложные формулы сокращенного умножения, в которых переменные возводятся в куб.Их использование может пригодиться в задачах повышенной сложности. Выведем их.

Найдем значение куба суммы двух слагаемых. Для этого возведем в куб выражение a + b:

(a + b) 3 = (a + b) 2 (a + b) = (a 2 + 2ab + b 2 )(a + b) = a 3 + a 2 b + 2a 2 b + 2ab 2 + ab 2 + b 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

которое называют формулой куба суммы.

Пример. Вычислите 101 3

101 3 = (100 + 1) 3 = 100 3 + 3*100 2 *1 + 3*100*1 2 + 1 = 1000000 + 30000 + 300 + 1 = 1030301

Решение. Воспользуемся формулой куба суммы:

(4p + 3k) 3 = (4p) 3 + 3*(4p) 2 *3k + 3*4p*(3k) 2 + (3k) 3 = 64p 3 + 144p 2 k + 108pk 2 + 27k 3

Выведем аналогичным образом и формулу куба разности чисел:

Итак, мы получили ещё одно тождество

Решение. Представим число 498 как разность 500 – 2. Тогда для вычисления можно воспользоваться выражением для вычисления куба разности:

Сложнее получить тождества для суммы и разности кубов, ведь напрямую найти разложить на множители выражение a 3 + b 3 довольно тяжело. К счастью, математикам удалось подобрать новые множители.

Сначала рассмотрим выражение

Оно отличается от квадрата суммы только одним слагаемым. Вместо 2ab стоит ab. Из-за этой схожести его называют неполным квадратом суммы.

Аналогично определяют и такое понятие, как неполный квадрат разности.

Теперь попробуем перемножить неполный квадрат суммы чисел a и b и их разность:

В результате нам удалось получить формулу разности кубов:

Теперь попробуем умножить сумму двух величин на неполный квадрат разности:

Получили формулу суммы кубов:

Понятно, что запомнить все эти тождества нелегко, однако их всегда можно посмотреть в любом математическом справочнике.

Решение. Здесь можно воспользоваться тождеством для куба суммы:

Далее для упрощения расчетов добавим к значению в скобке произведение 55•45 и тут же отнимем его. Это позволит сделать «дополнить» неполный квадрат разности и воспользоваться соответствующей формулой сокращенного умножения:

В свою очередь произведение 55•45 можно также упростить:

Полученный результат можно проверить с помощью калькулятора:

55 3 + 45 3 = 257500

Треугольник Паскаля

До этого мы нашли формулы сокращенного умножения, которые позволяют возводить бином (a + b) во вторую и третью степень. Интересно, что есть быстрый способ составить подобное тождество для возведения выражения (a + b) в любую натуральную степень. Для этого используется так называемый треугольник Паскаля. Справедливости ради сразу отметим, что Блез Паскаль описал его лишь в 1653 году, в то время как упоминание о таком треугольнике содержится в трудах китайца Чжу Шицзе (1303 г.), перса Омара Хайяма (1100 г.) и индийца Халаюдхи (Xвек).

Выглядит треугольник Паскаля так:

На вершине (его условно считают нулевым, а не первым уровнем) стоит число 1. На следующем (первом) уровне стоит уже две единицы. Изучим уровень ниже. Здесь уже три числа. По краям снова единицы, а в центре двойка. Обратите внимание, что двойка равна сумме тех 2 цифр, которые расположены над ней (1 и 1).

На следующем уровне уже 4 числа. Снова по краям единицы, а в других ячейках стоят такие числа, что они равны сумме двух чисел над собой (2 + 1 = 3).

По такому же принципу построен весь треугольник. Количество уровней в нем не ограничено, хотя на рисунке последним показан 10-ый уровень.

Итак, при построении треугольника Паскаля используются следующие правила:

Какое же отношение треугольник Паскаля имеет к формулам сокращенного умножения? Запишем тождества для возведения в различные степени бинома a + b, а рядом – числа из соответствующего уровня треугольника (их называют биноминальными коэффициентами):

Можно заметить, что числа в треугольнике совпадают с теми коэффициентами, которые есть в формуле сокращенного умножения:

(a + b) 6 = a 6 + 6a 5 b + 15a 4 b 2 + 20a 3 b 3 + 15a 2 b 4 + 6ab 5 + b 6

При этом степень каждого одночлена равна 6.

У треугольника Паскаля есть много других важных свойств, из-за которых он используется в иных разделах математики, в частности, в комбинаторике (она изучает количество способов, которыми можно расставить в определенном порядке предметы)и теории вероятностей. Например, можно заметить, что сумма всех чисел в строке n равна 2 n :

1 + 3 + 3 + 1 = 8 = 2 3

1 + 4 + 6 + 4 + 1 = 16 = 2 4

Более подробно использование треугольника Паскаля будет рассмотрено в старших классах.

Источник

Квадрат суммы и разности

Квадрат суммы

Выражение (a + b) 2 — это квадрат суммы чисел a и b. По определению степени выражение (a + b) 2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что

Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:

Многочлен a 2 + 2ab + b 2 называется разложением квадрата суммы.

Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых.

Пример. Возвести в квадрат выражение 3x 2 + 2xy.

Решение: Чтобы не производить дополнительных преобразований, воспользуемся формулой квадрата суммы. У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:

Квадрат разности

Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:

Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.

Пример. Представьте квадрат разности в виде трёхчлена:

Решение: Используя формулу квадрата разности, находим:

Теперь преобразуем выражение в многочлен стандартного вида:

Разность квадратов

Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.

Из правила следует, что общая формула разности квадратов выглядит так:

Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.

Пример. Преобразуйте произведение в двучлен:

В примере мы применили формулу разности квадратов справа налево, то есть, нам дана была правая часть формулы, а мы преобразовали её в левую:

На практике все три рассмотренные формулы применяются и слева направо, и справа налево, в зависимости от ситуации.

Источник