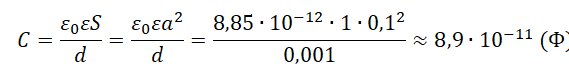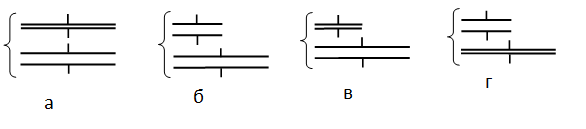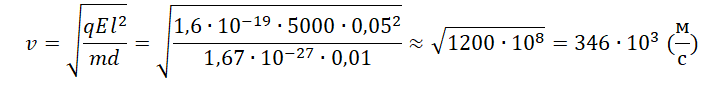Что такое разность потенциалов в конденсаторе

Что такое разность потенциалов в конденсаторе

Электрическая емкость

При сообщении проводнику заряда на его поверхности появляется потенциал φ, но если этот же заряд сообщить другому проводнику, то потенциал будет другой. Это зависит от геометрических параметров проводника. Но в любом случае потенциал φ пропорционален заряду q.

Коэффициент пропорциональности С называют электроемкостью – физическая величина, численно равная заряду, который необходимо сообщить проводнику для того, чтобы изменить его потенциал на единицу.

Единица измерения емкости в СИ – фарада. 1 Ф = 1Кл/1В.

Если потенциал поверхности шара

По этой формуле можно рассчитать емкость Земли. Если диэлектрическая проницаемость среды ε = 1 (воздух, вакуум) и то имеем, что C_З = 7·10 –4 Ф или 700 мкФ.

Чаще на практике используют более мелкие единицы емкости: 1 нФ (нанофарада) = 10 –9 Ф и 1пкФ (пикофарада) = 10 –12 Ф.

Необходимость в устройствах, накапливающих заряд, есть, а уединенные проводники обладают малой емкостью. Опытным путем было обнаружено, что электроемкость проводника увеличивается, если к нему поднести другой проводник – за счет явления электростатической индукции.

Конденсатор – это два проводника, называемые обкладками, расположенные близко друг к другу.

Конструкция такова, что внешние, окружающие конденсатор тела, не оказывают влияние на его электроемкость. Это будет выполняться, если электростатическое поле будет сосредоточено внутри конденсатора, между обкладками.

Конденсаторы бывают плоские, цилиндрические и сферические.

Так как электростатическое поле находится внутри конденсатора, то линии электрического смещения начинаются на положительной обкладке, заканчиваются на отрицательной, и никуда не исчезают. Следовательно, заряды на обкладках противоположны по знаку, но одинаковы по величине.

Емкость конденсатора равна отношению заряда к разности потенциалов между обкладками конденсатора:

Помимо емкости каждый конденсатор характеризуется U_раб (или U_пр.) – максимальное допустимое напряжение, выше которого происходит пробой между обкладками конденсатора.

Емкостные батареи – комбинации параллельных и последовательных соединений конденсаторов.

1) Параллельное соединение конденсаторов (рис. 5.9):

В данном случае общим является напряжение U:

.

Сравните с параллельным соединением сопротивлений R:

Таким образом, при параллельном соединении конденсаторов суммарная емкость

Общая емкость больше самой большой емкости, входящей в батарею.

2) Последовательное соединение конденсаторов (рис. 5.10):

Общим является заряд q.

или , отсюда

Сравните с последовательным соединением R:

Таким образом, при последовательном соединении конденсаторов общая емкость меньше самой маленькой емкости, входящей в батарею:

Расчет емкостей различных конденсаторов

1. Емкость плоского конденсатора

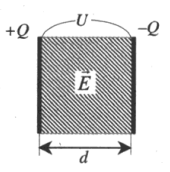
Напряженность поля внутри конденсатора (рис. 5.11):

Напряжение между обкладками:

где – расстояние между пластинами.

Так как заряд , то

Как видно из формулы, диэлектрическая проницаемость вещества очень сильно влияет на емкость конденсатора. Это можно увидеть и экспериментально: заряжаем электроскоп, подносим к нему металлическую пластину – получили конденсатор (за счет электростатической индукции, потенциал увеличился). Если внести между пластинами диэлектрик с ε, больше, чем у воздуха, то емкость конденсатора увеличится.

Из (5.4.6) можно получить единицы измерения ε₀:

2. Емкость цилиндрического конденсатора

Разность потенциалов между обкладками цилиндрического конденсатора, изображенного на рисунке 5.12, может быть рассчитана по формуле:

где λ – линейная плотность заряда,R₁ иR₂ – радиусы цилиндрических обкладок,l– длина конденсатора, .

Тогда, так как , получим

Понятно, что зазор между обкладками мал: то есть

Тогда

3. Емкость шарового конденсатора (рис. 5.13)

Из п. 3.6 мы знаем, что разность потенциала между обкладками равна:

Тогда, так как , получим

Это емкость шарового конденсатора, где R₁ и R₂ – радиусы шаров.

В шаровом конденсаторе – расстояние между обкладками. Тогда

Таким образом, емкость шарового конденсатора с достаточной степенью точности можно рассчитать так же, как и емкость плоского, и цилиндрического конденсаторов.

Источник

Конденсаторы

теория по физике 🧲 электростатика

Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.

Плоский конденсатор — система двух разноименно заряженных пластин.

Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:

Электроемкость конденсатора

Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.

Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).

Электроемкость конденсатора определяется формулой:

Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.

Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:

Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.

Энергия конденсатора

Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:

Подсказки к задачам

Конденсатор отключен от источника	q = q′
Конденсатор подключен к источнику	U = U′
Количество теплоты и энергия конденсатора	Q = ∆Wэ

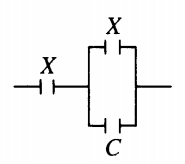
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.

Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.

Площадь квадратной пластины равна квадрату ее стороны:

Соединения конденсаторов

Подсказки к задачам

Последовательное соединение	Параллельное соединение
Схема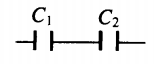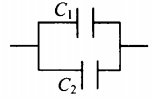
Напряжение

Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами.

Схема соединения конденсаторов одноименными полюсами: 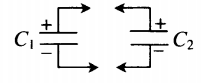Заряд системы после соединения:

q′ = C 1 U 1 + C 2 U 2

Электрическая емкость системы:

Два конденсатора, электроемкости которых C₁ и C₂, заряжены до напряжения U₁ и U₂. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами.

Схема соединения конденсаторов разноименными полюсами:

Заряд системы после соединения:

q′ = C 1 U 1 − C 2 U 2

Электрическая емкость системы:

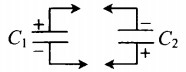
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.

Электрическая емкость параллельного соединения равна:

Электроемкость последовательного соединения:

Учтем, что суммарная электроемкость равна C:

Преобразуем, умножим выражение на CX(X+C):

X ( X + C ) = C X + C ( X + C )

X 2 + X C = C X + C X + C 2

Решив уравнение, получим: X = 25,9 пФ.

Разбор задач на тему «Заряженная частица в поле конденсатора»

Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U?

Условие равновесия исходит из второго закона Ньютона:

− F т я ж + − F K + − F A = 0

Проекция второго закона Ньютона на ось ОУ:

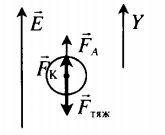
Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения:

Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения:

Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l?

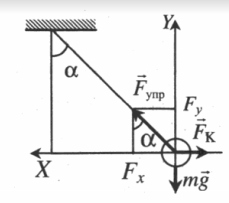
Условие равновесия исходит из второго закона Ньютона:

− F т я ж + − F K + − F у п р = 0

Проекции на оси ОХ и ОУ соответственно:

Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их:

Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь.Второй закон Ньютона в векторной форме:

Проекция на вертикальную ось:

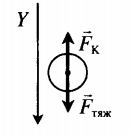
− F т я ж + − F K = m − a

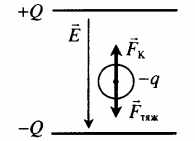
Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок:

Если F_тяж > F_K, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны:

Начальная скорость шарика равна нулю. Поэтому перемещение также равно:

Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого − E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер.Второй закон Ньютона в векторной форме:

− F т я ж + − F K = m − a

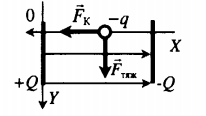
Если сила Кулона направлена вправо, то s_x = d.

Если сила Кулона направлена вправо, то s_x = b.

Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево.

Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно:

Проекции перемещений на эти же оси:

Так как время движения шарика по вертикали и горизонтали одинаково:

Введите ответ в поле ввода Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Емкость конденсатора определяется формулой:

Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.

Вот как взаимосвязана электроемкость и заряд конденсатора:

Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.

С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.

Алгоритм решения

Решение

На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.

На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:

S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.

Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.

На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:

Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?

Алгоритм решения

Решение

Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Ответ записать в км/с, округлив до десятков.

Алгоритм решения

Решение

Запишем исходные данные:

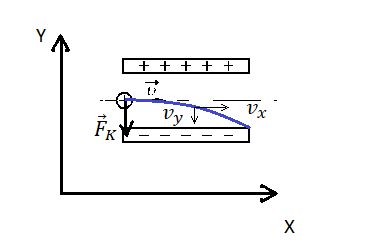
Изначально протон обладает только горизонтальной скоростью v, равной v_x. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.

Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью v_x:

Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):

Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:

Приравняем правые части уравнений времени и получим:

Отсюда скорость равна:

Ускорение выразим из второго закона Ньютона:

Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙10 3 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник