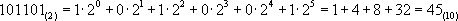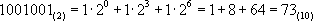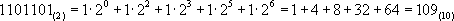Что такое разрядная сетка пэвм и как она влияет на результат
Как переводить числа в восьмеричную систему счисления
Во время изучения информатики не всем понятно, как переводить в восьмеричную систему счисления десятичную форму представления. В школьной программе применяется обыкновенная общая методика, но при этом не учитываются умственные способности учеников. Специалисты разработали специальный алгоритм, позволяющий выполнить эту операцию без особых усилий. Однако для начала нужно изучить теорию, а затем перейти к ее практическому применению.
Общие сведения
Для кодирования информации используются различные формы представления данных. Это объясняется тем, что компьютер «не понимает» обыкновенного человеческого языка напрямую. Любая команда переводится в машинный код при помощи специальных алгоритмов кодирования данных. Чтобы в них разобраться, нужно освоить базовые понятия, к которым относятся следующие:
Следует отметить, что каждый пункт необходимо подробно разобрать, поскольку от этого зависит корректность применения алгоритма. Далее нужно ознакомиться с понятием разрядной сетки.
Разрядная сетка
Разрядной сеткой называется совокупность цифр, расположенных в определенном порядке значимости элементов. На первый взгляд, определение является сложным для понимания. Однако это не так. Чтобы в этом убедиться, необходимо разобрать число «126789». Оно состоит из компонентов, которые называются цифрами, где каждая принимает значение из диапазона от 0 до 9. Любая из них находится на определенном месте, а именно:
Следует отметить, что значимость элементов определяется очень просто. Для этого нужно сравнить для примера сотни и единицы. Первые больше, чем вторые. На основании этого примера утверждение о значимости доказано.
Компоненты разрядной сетки можно сложить, т. е. 1*9+10*8+100*7+1000*6+10000*2+100000*1=126789. Каждое число состоит из цифр. В этом и заключается основное отличие между ними. Теперь можно переходить к знакомству с системами счисления.
Виды систем счисления
Системы счисления условно делятся на две группы. К ним относятся следующие:
В первом случае расположение математических символов (цифр) играет важную роль, поскольку влияет на величину числа в целом. Чтобы в этом убедиться, нужно разобрать значение в десятичном формате 192. Для опыта необходимо переставить знаки. При этом получаются пять числовых величин:
Следует отметить, что каждое из них отличается от другого. Все пять чисел можно также сравнить с исходным значением. Из выполненного опыта можно сделать вывод, что расположение компонентов в разрядной сетке имеет значение. К позиционным СС относятся следующие основные формы представления чисел:
Однако существуют и другие формы представления числовых величин, а именно: третичная, четвертичная, пятеричная и т. д. Основным их отличием является основание.
Унарными называются такие СС, какие не зависят от расположения символов. Для примера необходимо вспомнить фильм о Робинзоне Крузо. Он считал дни при помощи обыкновенных палочек, которые чертил на поверхности.
Другим примером является подсчет количества мешков сахара, погруженных на грузовую машину. При загрузке одного мешка бригадир ставит обыкновенный произвольный символ, обозначающий единицу. У каждой системы счисления существует определенный алфавит или символы, используемые для записи цифр и чисел.
Чтобы перевести величину в позиционную восьмеричную СС, необходимо освоить методику конвертации и работы с двоичным кодом.
Двоичный код
Перед тем как начать работу с восьмеричным кодом нужно ознакомиться с двоичным. Чтобы перевести число из десятичной формы в двоичную, требуется воспользоваться следующим алгоритмом:
Обратная операция выполняется по более упрощенной методике. Она имеет такой вид:
Следует отметить, что проверить конвертацию можно при помощи специальных калькуляторов. Последние должны работать с двоичным, восьмеричным и шестнадцатеричным кодами. После освоения материала работы с двоичной формой представления числа можно перейти к восьмеричной.
Восьмеричная форма
Восьмеричная система исчисления применяется в программировании. Однако чтобы в нее перевести десятичную величину, нужно ознакомиться с методикой, позволяющей выполнить эту операцию. Она имеет следующий вид:
Чтобы разобраться в теории, необходимо использовать алгоритм на практическом примере перевода десятичной формы в виде числа 19 в восьмеричный код. Получение искомого результата нужно осуществлять по такой методике:
Для обратного преобразования применяется также определенные правила, составляющие в совокупности отдельный алгоритм. Он выглядит таким образом:
Для примера необходимо рассмотреть величину, равную [23]<8>. Чтобы ее перевести обратно на «человеческий понятный язык» (запись в десятичной форме), следует применить такой алгоритм:
Следует отметить, что в третьем пункте для удобства может не присутствовать нуль, поскольку у двоичного кода есть одно важное правило: если дописывать нули слева, то это действие не повлияет на исходное число.
Кроме того, математики не рекомендуют составлять таблицу для восьмеричной системы счисления, поскольку в этом нет необходимости, как для шестнадцатеричного кода. Для удобства можно записать все методики на отдельные листы бумаги, которые должны находиться постоянно перед глазами ученика.
Таким образом, восьмеричная система представления чисел применяется для кодирования информации в программировании и вычислительной технике. Для этого необходимо получить базовые знания о специальных методиках конвертации величин.
Большая Энциклопедия Нефти и Газа
Разрядная сетка
Разрядная сетка при операциях с фиксированной запятой в значительно большей степени, чем при работе с плавающей запятой, влияет на точность представления чисел. Чем больше разрядов в ячейке памяти, тем с большей точностью ( с большим количеством знаков) может быть записано в ней число. [1]
Разрядная сетка ЭВМ и форма представления числовой информации однозначно определяют диапазон представляемых в ЭВМ чисел и как следствие точность получаемых результатов. [5]
Разрядные сетки памяти одноадресной и трехадресной ЭЦВМ, для которых написан порядок выполнения некоторых команд, обеспечивают требуемую точность расчетов при решении практических тяговых задач и при выполнении исследований в этой области. Размещение чисел и команд в сумматоре соответствует распределению разрядов в ячейках оперативной памяти. [6]
Разрядная сетка ЭВМ и форма представления числовой информации однозначно определяют диапазон представляемых в ЭВМ чисел и как следствие точность получаемых результатов. [8]
Если разрядная сетка ЭВМ не позволяет хранить обе координаты в одной ячейке, то все усложняется. Координаты х и у должны передаваться в дисплей отдельными командами, и необходимо иметь третью команду для подсвечивания точки. [9]
Переполнение разрядной сетки той части сумматора, которая отведена для оперирования мантиссами, не мешает получению искомой суммы или разности. Переполнение разрядной сетки в целом после сложения или вычитания может произойти только при увеличении порядка п2 на 1 и заключается в переполнении той части разрядной сетки, которая отведена под порядок. [10]
Переполнение разрядной сетки при сложении s модифицированных машинных кодах обнаруживается способом сравнения знаковых разрядов полученной суммы. [11]
Переполнение разрядной сетки возможно при сложении операндов с одинаковыми знаками. Оно может быть определено по наличию переноса из старшей тетрады. При выполнении операции вычитания меняется знак второго операнда, после чего действия над десятичными числами производятся так же, как и при сложении. [12]
Переполнение разрядной сетки может наступить только при сложении чисел одинакового знака. [13]
Переполнение разрядной сетки той части сумматора, которая отведена для оперирования мантиссами, не мешает получению искомой суммы или разности. Переполнение разрядной сетки в целом после сложения или вычитания может произойти только при увеличении порядка я2 на 1 и заключается в переполнении той части разрядной сетки, которая отведена под порядок. [14]
Таблица двоичной системы счисления для информатики 8 класса
Конвертация форм представления чисел осуществляется различными способами. Одним из них считается перевод десятичного значения в двоичную систему счисления по таблице. В 8 классе на информатике изучаются специальные методики для работы с величинами, а именно — их преобразование на машинный язык. Для этой цели специалисты разработали специальный алгоритм.
Общие сведения
Двоичная форма представления информации используется для кодирования данных. Ее также называют бинарной. Она связана с историей развития вычислительной техники, когда применялись различные логические элементы с двумя состояниями, а именно: 0 — отсутствие и 1 — наличие. Например, при протекании тока через катушку индуктивности происходит возникновение магнитного поля (оно будет присутствовать в соленоиде), а значит, этот процесс можно декодировать, как «1».
С изобретением полупроводниковых приборов (транзисторов) габариты вычислительных средств существенно снизились. Значительной минимизации удалось достигнуть благодаря изобретению интегральных микросхем, которые обладали регистрами памяти. В них можно было записывать различную информацию.
Однако двоичная система является только одной из форм представления числовых значений. Специалисты рекомендуют ознакомиться с классификацией систем представления величин, поскольку этот аспект позволит понять саму суть кодирования информации.
Разрядная сетка
Каждое число состоит из цифр, объединенных в разрядную сетку. Последняя состоит из элементов, имеющих определенный весовой коэффициент. Однако не всем такие факты будут понятны. В этом случае специалисты в IT-сфере рекомендуют ознакомиться с числом «8236410». Оно состоит из цифр и является примером значения в десятеричном коде.
Записывается величина в таком формате: [8236410]<10>. Однако для упрощения принято писать просто число без скобок квадратного типа и указания типа системы представления числа, т. е. 8236410. Далее необходимо разложить его на составные элементы в виде такого списка:
Совокупность всех семи компонентов и называется разрядной сеткой. Если проанализировать все ее элементы, то можно сделать выводы:
Следует отметить, что величину 8236410 возможно представить в таком виде: 0*10^0 + 1*10^1 + 4*10^2 + 6*10^3 + 3*10^4 + 2*10^5 + 8*10^6=0+10+400+6000+30000+200000+6000000=8236410.
Любое число представляется в определенной системе исчисления. Последние делятся на отдельные группы. Далее нужно разобрать их классификацию.
Классификация систем счисления
Системы счисления условно классифицируются на два вида. К ним относятся следующие в зависимости от наличия разрядной сетки и влияния на ее значение:
Первые называются также позиционными формами представления. Они состоят из четкой разрядной сетки, элементы которой зависят от расположения. Примерами являются следующие: двоичные, восьмеричные и шестнадцатеричные. Положение их компонентов влияет на значение самой величины.
Для демонстрации зависимости величины от размещения разрядов специалисты рекомендуют разобрать число 134. В последнем необходимо переставить цифры местами. В результате этого получатся такие величины:
Если выполнить аналогичную операцию для остальных четырех величин, то будут получены также ненулевые числа. Следовательно, утверждение доказано.
Вторым типом представления чисел являются унарные системы счисления. Они не имеют разрядной сетки. В них наблюдается полное соответствие каждого компонента одному значению. Данная форма удобна при подсчете выполненных элементов какой-либо операции. Например, погрузка мешков цемента в машину.
При подсчете количества применяются специальные математические символы в виде палочек, звездочек и т. д. Каждый из элементов соответствует определенному числу. Например, один мешок, погруженный в машину, обозначается палочкой, а десять — звездочкой.
Следует отметить, что на начальной стадии изучения является двоичная система счисления, примером которой считается величина [1100100]<2>. Это значение эквивалентно числу в десятичном формате «100». Далее необходимо разобрать практическое использование двоичного (бинарного) кода в сфере информационных технологий.
Применение двоичного кода
Бинарный код является базовым. С его помощью можно осуществлять кодирование в другие системы представления, а именно: 8-ричную и 16-ричную. Двоичная система позволяет кодировать незначительные объемы информации, поскольку обладает наименьшей мощностью среди остальных способов декодирования информации.
Кроме того, бинарное счисление применяется при построении различных условий в программировании при написании программных продуктов. Оно очень часто используется в логических конструкциях. Одной из них является «IF-ELSE», в которой переменная или выражение может принимать только значения истины (1) или лжи (0).
При проектировании различных устройств для прошивки микроконтроллера также применяется бинарный код. Например, стиральная машинка-автомат при запуске выполняет определенную программу, записанную в специальной флеш-памяти.
Чтобы повысить возможности той или иной вычислительной системы, необходимо применять 8-ричную и 16-ричную системы счисления. Они позволяют работать с большим массивом данных. Конвертация в них выполняется по определенным этапам:
Для таких операций предусмотрены два способа кодирования. Далее нужно разобрать самый простой из них — методику деления столбиком.
Методика преобразования делением
Алгоритм деления в столбик при переводе десятичной формы в двоичную является самым простым. Его суть заключается в делении искомой величины на основание системы, т. е. двойку. Он имеет следующий вид:
Для понимания методики необходимо перевести величину 100 в двоичный код. Это выполняется следующим образом:
Операция обратного преобразования является очень простой. Для этого необходимо сложить элементы разрядной сетки с учетом коэффициентов, т. е. 0*2^0+0*2^1+1*2^2+0*2^3+0*2^4+1*2^5+1*2^6. Если подсчитать все элементы числового выражения, то получится значение, равное сотне. Однако это не единственный алгоритм перевода. Далее нужно рассмотреть методику степеней.
Алгоритм декодирования степенью
Методика степеней позволяет решать задачи конвертации десятичной величины в двоичный код при помощи специальной таблицы двоичных чисел. Она может быть представлена и списком. Последний имеет следующий вид:
Для конвертации применяется определенная методика. Она имеет следующий вид:
Чтобы разобраться в алгоритме, необходимо реализовать его на практическом примере. Конвертация числа десятичного формата в двоичный при помощи степенной методики имеет такой вид:
Следует отметить, что проверка правильности решения (обратная операция конвертирования) применяется так, как и в алгоритме конвертации посредством деления в столбик. Кроме того, результат можно проверить также при помощи онлайн-калькулятора, поддерживающего формы представления информации.
Таким образом, двоичный код применяется в вычислительной технике для кодирования информации на машинный язык, а также для преобразования в восьмеричную и шестнадцатеричную формы представления чисел.
ХНУРЭ дистанционное обучение
Новости сайта
Студентам, хто досі не має доступ до необхідних, за розкладом, навчальних дисциплін.
Шановні студенти ХНУРЕ.
Оголошення для тих, хто досі не має доступ до необхідних, за розкладом, навчальних дисциплін.
Ми не можемо підключати студентів до навчальних дисциплін на вимогу студента.
Ми підключаємо студентів тільки за заявкою викладача.
Тому, будь ласка, зверніться до викладачів тих курсів, доступу до яких у вас немає, щоб вони написали нам лист зі списком студентів, яких потрібно додати на їх дисципліну.
Внимание первокурсников!
Обратите внимание, что хотя логины для почты и системы “ХНУРЭ Дистанционное обучение” одинаковые, но пароли разные!
Новый пароль должен быть не менее 8 символов, в нем должны быть минимум 1 цифра, 1 буква в нижнем регистре и 1 буква в верхнем регистре.
Забыли или потеряли пароль?
Если Вы были зарегистрированы в нашей системе и помните свой логин (он же адрес электронной почты в домене @nure.ua), на который был зарегистрирован ваш аккаунт, воспользуйтесь системой автоматического восстановления пароля:
Восстановить пароль от dl.nure.ua
Восстановить пароль от почты можно в комнате 282 по студенческому билету.
ВНИМАНИЕ! сотрудники ЦТДО не работают со студентами напрямую, а только через ответственных за ДО. Все обращения в очную или при помощи писем на адреса сотрудников – обрабатываться не будут.
Способы представления чисел в разрядной сетке ЭВМ
Для хранения чисел в памяти компьютера используется два формата: целочисленный (естественная форма) и с плавающей точкой (нормализованная форма) (точка — разделительный знак для целой и дробной части числа).
Целочисленный формат (формат с фиксированной точкой) используется для представления в компьютере целых (англ. integer) положительных и отрицательных чисел. Для этого, как правило, используются форматы, кратные байту: 1, 2, 4 байта.
В форме с фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (или точки), отделяющей целую часть от дробной.
Эта форма проста и привычна для большинства пользователей, но имеет небольшой диапазон представления чисел и поэтому не всегда пригодна при вычислениях. Если же в результате какой-либо арифметической операции получается число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, и все дальнейшие вычисления теряют смысл.
Однобайтовое представление применяется только для положительных целых чисел. В этом формате отсутствует знаковый разряд. Наибольшее двоичное число, которое может быть записано при помощи 1 байта, равно 11111111, что в десятичной системе счисления соответствует числу 25510.
Самое большое (по модулю) целое число со знаком, которое может поместиться в 2-байтовом формате, это число 0111111111111111, то есть при помощи подобного кодирования можно представить числа от −32 76810 до 32 76710.
Если число вышло за указанные границы, произойдет переполнение! Поэтому при работе с большими целыми числами под них выделяется больше места, например 4 байта.
Формат с плавающей точкой (нормализованная форма) используется для представления в компьютере действительных чисел (англ. real). Числа с плавающей точкой размещаются, как правило, в 4 или 8 байтах.
Нормализованная форма представления чисел обеспечивает огромный диапазон их записи и является основной в современных ЭВМ.
Представление целого положительного числа в компьютере
Для представления целого положительного числа в компьютере используется следующее правило:
— число переводится в двоичную систему;
— результат дополняется нулями слева в пределах выбранного формата;
— последний разряд слева является знаковым, в положительном числе он равен 0.
Представление целого отрицательного числа в компьютере
Для представления целого отрицательного числа в компьютере используется дополнительный код. Такое представление позволяет заменить операцию вычитания числа операцией сложения с дополнительным кодом этого числа. Знаковый разряд целых отрицательных чисел всегда равен 1.
Для представления целого отрицательного числа в компьютере используется следующее правило:
— к полученному коду прибавляется 1.
Обратный код для положительного двоичного числа совпадает с его прямым кодом, а для отрицательного числа нужно во всех разрядах, кроме знакового, нули заменить единицами и наоборот.
Дополнительный код для положительного числа совпадает с его прямым кодом, а для отрицательного числа образуется путем прибавления 1 к обратному коду.
Отрицательное число может быть представлено в виде 2 или 4 байт.
Например, представим число −13510 в 2-байтовом формате:
— 13510 → 10000111 (перевод десятичного числа без знака в двоичный код);
— 0000000010000111(дополнение двоичного числа нулями слева в пределах формата);
— 0000000010000111 → 1111111101111000(перевод в обратный код);
— 1111111101111000 → 1111111101111001 (перевод в дополнительный код).
Представление вещественного (действительного) числа в компьютере
Вещественное число может быть представлено в экспоненциальном виде, например:
В этом формате вещественное число (R) представляется в виде произведения мантиссы (m) и основания системы счисления (P) в целой степени (n), называемой порядком.
Задания для самостоятельного решения
Задание 1 Получить десятичный эквивалент для двоичных чисел.
Перевод числа из двоичной в десятичную систему счисления выполняется только представлением его в развёрнутой форме.
Варианты заданий для самостоятельного выполнения