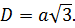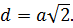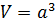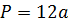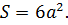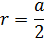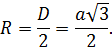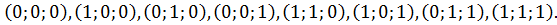Что такое ребро куба 3 класс
Урок математики в 3 классе «Геометрические фигуры. Куб и его изображение»
У рок математики
3 класс Учитель Белая Л. А.
Тема: КУБ И ЕГО ИЗОБРАЖЕНИЕ
Цели и задачи: сформировать представление о кубе и его изображении; закрепить понятия «грань», «ребро», «вершина» куба. Закреплять умение решать задачи, совершенствовать математические навыки, учить рассуждать, анализировать, обобщать. Формировать способность к выделению существенных признаков объектов, к построению нового способа действий на основе аналогии, к самоконтролю и самооценки. Развивать познавательные интересы, творческие способности, логическое мышление, речь, внимание, дисциплину.
Ход урока
I. Организационный момент
II. Постановка задач и целей урока
1. – Для того, чтобы наш урок прошёл успешно какие задачи поставим перед собой?
(Познакомиться с новой темой; продолжать учиться решать задачи; учиться правильно вычислять, сравнивать; внимательно слушать и слышать и т. д.)
— К нам на урок пришла точка. Как вы думаете в связи с чем она пришла сегодня на урок? О чём узнаем?
(Будем говорить о геометрических фигурах)
— Какие геометрические фигуры вы уже знаете?
— На какие группы их можно разделить?
(Плоские и объёмные (пространственные)
2. –Сегодня мы познакомимся с одной объёмной фигурой. Чтобы узнать с какой фигурой познакомимся выполним математический диктант.
Математический диктант
5. Найдите Р треугольника, у которого все стороны равны. Длина одной стороны 9 см. (27см)
6. Найдите Р квадрата со стороной 6см. (36см)
7. Найдите площадь прямоугольника со сторонами 6м и 40м. (240м)
8. Найдите Р прямоугольника со сторонами 9см и 15см. (48см)
9. Найдите сторону прямоугольника, одна сторона которого 20м, а площадь 180м. кв. (9м)
Соединяем последовательно точки
— Что за фигура у нас получилась? (Куб)
— Какая это фигура? (Объёмная)
Ш. Работа над темой урока
(Открываю запись темы урока на доске и раздаю кубы на парты)
2. – У вас на партах кубы. Рассмотрите их. Что можете сказать об этой геометрической фигуре? Можете провести измерение.
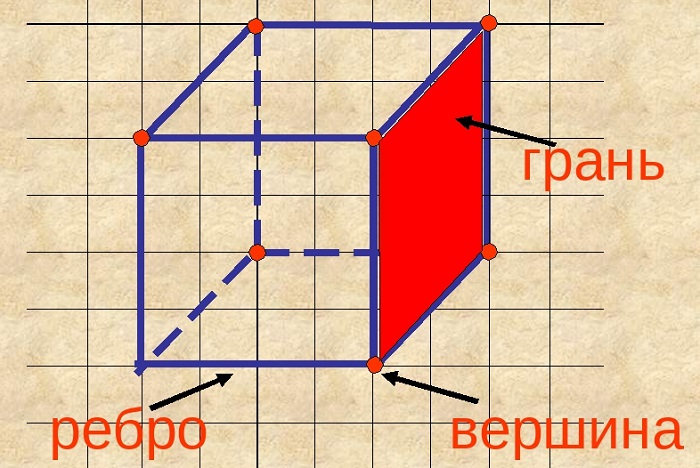
— Эти стороны – грани. Посчитайте сколько всего граней у куба? (6)
— Сколько всего вершин? (8)
— Сколько всего рёбер? (12)
3. Проблемная ситуация.
— Посмотрите на изображение куба на чертеже. Сколько всего граней, вершин, рёбер вы видите на чертеже?
(3-грани, 7-вершин, 9-рёбер)
— Почему же их меньше? (ответы детей)
— Стороны, которые мы не можем увидеть, обозначаются на чертеже пунктирной линией. Сейчас попробуем достроить правильное изображение куба.
На чертеже есть точка 9. попробуйте её соединить с точками, чтобы завершить построение куба.
— Кто знает с какими точками надо соединить точку 9? (27, 40, 180)
— Сколько теперь граней получилось? Вершин? Рёбер?
4. – Куб – это геометрическая фигура. Значит, что мы можем измерить? (длину, ширину рёбер)
— Измерьте. Что вы заметили?
— Если рёбра все равны, то какой фигурой является каждая грань?
— Найдите площадь одной грани.
— Чему равна площадь всей поверхности куба? Как быстро посчитать?
1.– Если я называю плоские фигуры – приседаем, если объёмные – делаем хлопок над головой.
2. –Подпрыгните столько раз:
а) сколько сторон у треугольника (3)
б) сколько вершин у круга (0)
в) сколько углов у квадрата (4)
г) сколько осей симметрии у прямоугольника (4)
5. Практическая работа
— Из трубочек (для коктейля) и пластилина сделаем модель куба. (каркас)
— Вычислите: Сколько потребуется проволоки, если этот каркас делать из проволоки?
— Какие измерения для этого надо сделать? Что надо знать?
— Как будем вычислять?
(Количество рёбер умножить на длину ребра)
6. Постановка задач на следующий урок.
— Кто знает как называется эта фигура?
— Чем она похожа с кубом?
— На эти вопросы мы ответим на следующем уроке.
7. «Точка» на приготовила ещё одно интересное задание.
— Рассмотрите сколько всего четырёхугольников изображено на рисунке? (треугольников)
IV. Подведение итогов урока
— Что нового узнали на уроке?
— Что было интересным?
— Что вызвало затруднения?
— Кто доволен своей работой?
_ Оцените на шкале успеха свои достижения. Если всё удалось, получилось – красным цветом; если всё было хорошо, но что – то не получилось– зелёным цветом; если не очень старался – синим.
«Изображение и фантазия». Урок изобразительного искусства во 2 классе Тема : ИЗОБРАЖЕНИЕ И ФАНТАЗИЯ. 2 класс – 30 мин. Вид занятий: рисование по памяти и представлению /по заранее заготовленной форме, путешествие.
Урок математики в 1 классе «Понятия больше, меньше, столько же и различные приемы сравнения множеств по этим признакам» Технологическая карта урока математики Учитель: Антинг Валентина Германовна Дата проведения: 17. 09. 2014 г. Класс: 1а Тема. Понятия «больше»,.


Урок математики в 3 классе «Умножение суммы на число» УМК «Школа России» муниципальное бюджетное общеобразовательное учреждение «Ивановская основная школа» Проект урока по математике.
Урок математики в 4 классе по теме «Деление на трехзначное число» Тема: Деление на трехзначное число Цель: закрепление умения делить многозначные числа на трехзначное с использованием алгоритма деления.
Урок математики во 2 классе на тему «Свойства сложения» Тема: «Свойства сложения» Цель: Знакомство со свойствами сложения (переместительным и сочетательным). Совершенствовать вычислительные навыки.
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
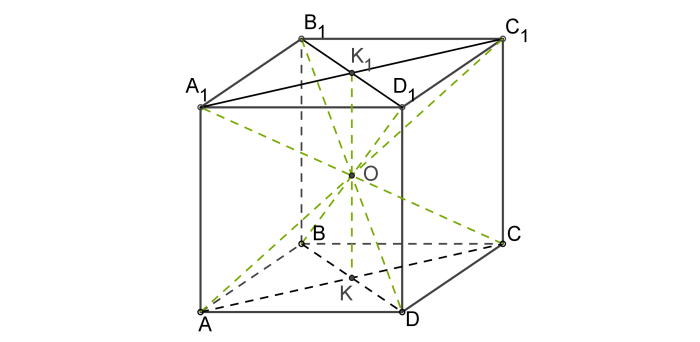
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
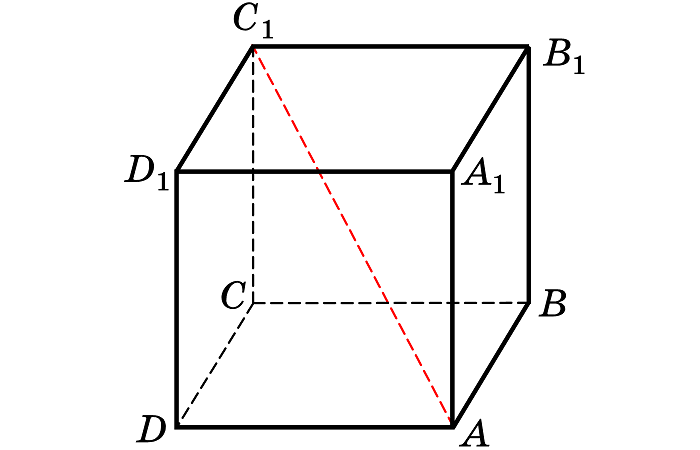
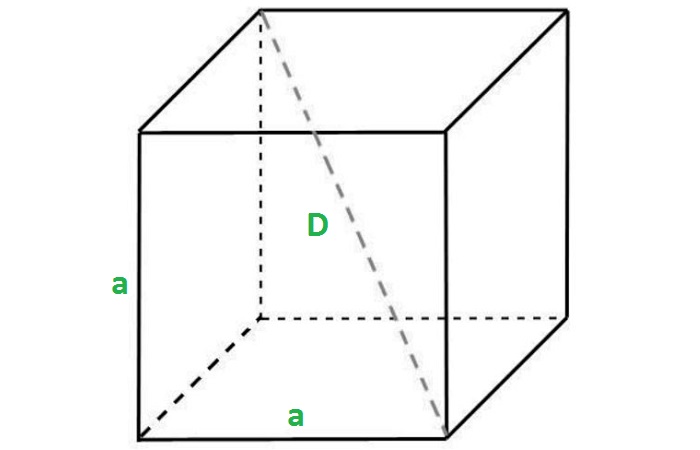
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
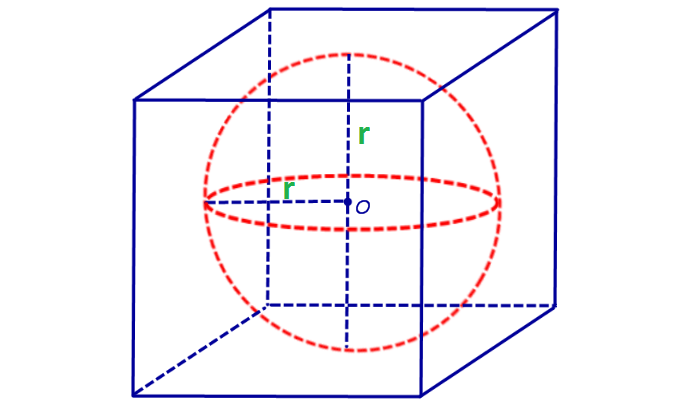
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
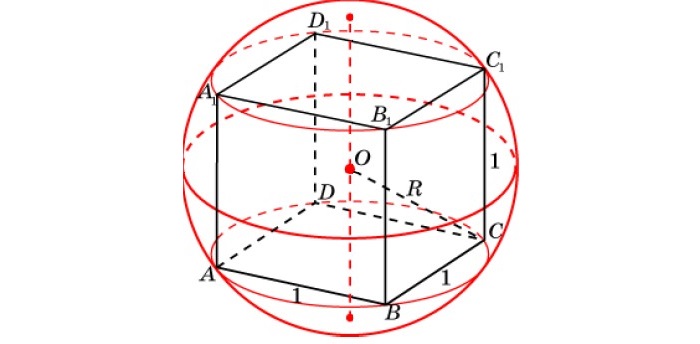
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
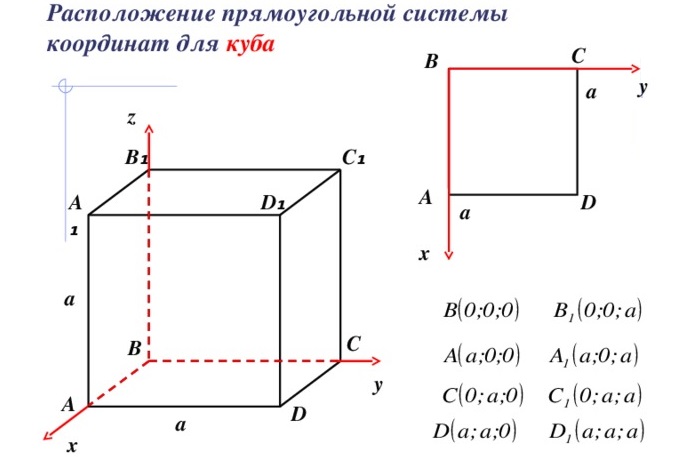
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
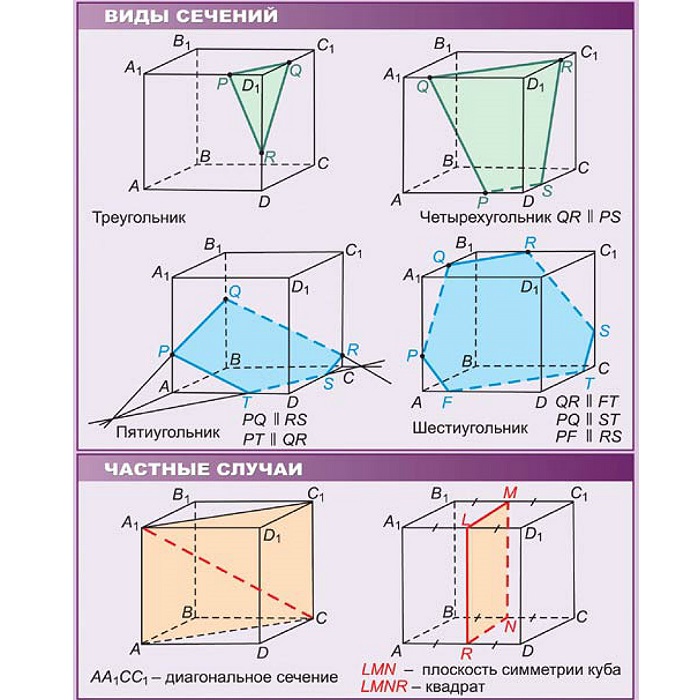
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
Свойство 3
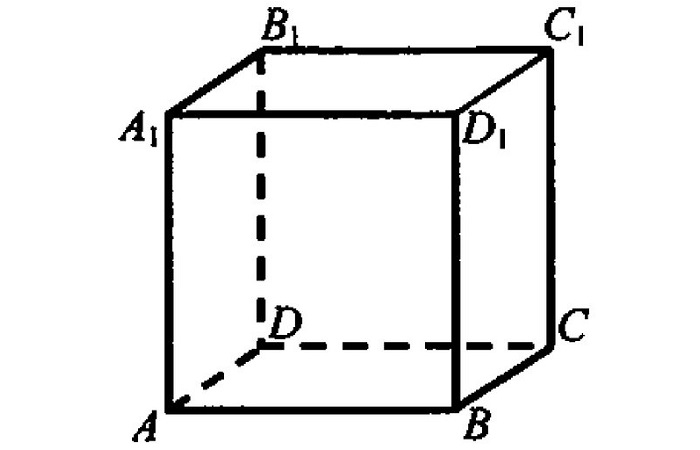
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Урок математики в 3-м классе «Куб. Элементы куба: грани, ребра, вершины. Развертка куба»
1. Организационный момент.
2. Актуализация опорных знаний
Появляется на экране мультимедийная презентация.
Рассмотрите геометрические фигуры. В них записаны математические выражения. Вычислите значение числового выражения, которое находится:
а) на пересечении круга и прямоугольника?
— Какое правило применили? (Деление числа на произведение)
в) Выражение, которое находится на пересечении квадрата и прямоугольника?
г) Выражение, которое находится в левом полукруге?
— Каким правилом пользовались?
(Умножение числа на произведение)
д) Выражение, которое содержится в ромбе, но не содержится в квадрате.
8 дм 4 см * 3= 84 см *3= 252см= 25 дм 2 см
— У каких этих фигур мы можем найти периметр?
— У каких фигур можем определить периметр несколькими способами?
На экране появляются слайд с формулами.
— Как найти периметр квадрата?
— А как найти площадь у прямоугольника?
— Как найти площадь у квадрата?
Обобщение: Вы хорошо знаете геометрические фигуры и вычисляете выражения. Знаете правила нахождения площади и периметра. Это нам необходимо для решения задач.
3. Постановка учебной задачи.
— Что общего у этих фигур (Плоские)
— Какие еще могут быть фигуры, кроме плоских? (Объемные)
— С каким геометрическим телом уже знакомы? (Параллелепипедом)
4. Закрепление изученного
А сейчас решим задачу из учебника.
— Можем сразу найти площадь квадрата? (Нет)
— Почему? (Не знаем сторону квадрата)
— Как узнать? ( 36:4=9 мм)
— Какой формулой мы будем пользоваться для нахождения площади квадрата?
— Решим эту задачу с комментированием?
— Начертите этот квадрат.
— Что вы знаете о прямоугольнике?
*Противоположные стороны равны.
*Диагонали прямоугольника равны.
*Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам.
— Решите задачу следующую задачу.
— Можем сразу ответить на вопрос? (Да)
— Как? ( площадь разделить на ширину)
Д/в. Что вы знаете о квадрате?
*Диагонали квадрата равны.
*Диагонали пересекаются и точкой пересечения делятся пополам.
*Диагонали квадрата пересекаются под прямым углом.
— Составьте обратные задачи данной.
5. Самостоятельная работа
— Можем сразу ответить на требование задачи? (Да)
— Как? (площадь разделить на длину)
— Эту задачу решит 1 вариант.
Кто выполнит задачу, решит дополнительно. Задание по своим силам, по выбору?
— Составим вторую задачу.
Длина участка прямоугольной формы 86 метров, ширина 40 м. Найдите площадь участка?
— Какой формулой будем пользоваться?( S квадрата = a * b)
— Дополнительно решите еще карточку по выбору
На каждой парте лежат дифференцированные задания.
Проверка самостоятельной работы.
В момент ответа учеников на экране появляются названные фигуры.
— Что такое трапеция?
*Это четырехугольник, у которого параллельны только 2 стороны.
— Что такое параллелограмм?
* Это четырехугольник, у которого все противоположные стороны равны и параллельны.
6. Физминутка.
Немного отдохнем, поработаем устно с геопланами. (У каждого ученика на парте) Нужно узнать фигуру по описанию. Прежде, чем начнем работать, используя таблицу, оцените свои знания, выберите круг нужного цвета. Будьте внимательны, мы учимся самоконтролю!
(На экране появляется таблица )
(Один ученик работает на магнитной доске, остальные с геопланами)
Проверка на магнитной доске
— Какая фигура здесь лишняя. не относится к многоугольникам? (Угол)
— Какие бывают углы? (Остроугольные, тупоугольные, прямоугольные)
— У кого сошлась самооценка?
— Кто ошибся в оценке себя?
— В чем допустили ошибки?
ВЫВОД: Будьте внимательны, мы учимся самоконтролю.
8. Графический диктант
Новые понятия появляются на экране.
— Сейчас мы выполним графический диктант и узнаем с каким геометрическим телом мы познакомимся на уроке.
— Поставьте точку, обозначьте ее латинской буквой А, затем отсчитайте 5 клеточек вправо, обозначьте буквой B, от В пять клеточек вверх, обозначьте буквой С, от этой точки 5 клеточек влево, обозначьте буквой Д; от А 3 клеточки по диагонали вправо вверх обозначьте Е; от В по диагонали вправо вверх 3 клеточки, обозначьте F, от Д вправо вверх 3 клеточки по диагонали обозначьте К, от С вправо вверх по диагонали 3 клеточки, обозначьте М.
9. Знакомство с кубом.
— Как называется это геометрическое тело? (КУБ)
*Это слово иностранное, иначе его называют шестигранник.
— Где вы встречали куб? (игра «Кубик Рубика», кубики для игры, кубики конструктора.)
Вот каркас куба из проволоки
(Помощники раздают кубики)
— Возьмите куб. положите его на левую руку.
Какой фигурой является грань куба? (Квадрат)
Поверхность каждого куба состоит из квадратов, которые называются ГРАНЬ.
— Почему он называется правильным шестиугольником?
— Сосчитайте грани куба. Сколько их? (6)
— Две соседние грани квадрата (многогранника) называются РЕБРОМ.
— Покажите ручкой (указкой) ребро
— Сосчитайте сколько у куба ребер? (12)
— Равны ли ребра по длине? (да)
— Сколько ребер пересекается (сходится) к одной вершине? (3)
— Сосчитайте сколько вершин у куба? (8)
Работа в тетради на печатной основе (стр. 8, зад. 12,13)
Изготовление развертки куба по технологической инструкции.
Появляется на экране:
— Сейчас мы сами изготовим развертку куба. Что такое развертка?
*Это как бы разрезанный куб на бумаге. (Показать)
НАПОМНИТЬ об осторожном обращении с ножницами, клеем, экономии бумаги.
— Покажите на кубе его вершины, ребра, грани.
Конструирование из кубов группами
Давайте вспомним правила работы в группах (внимательно слушай товарища, говори по очереди, не перебивай друга, помоги товарищу.
— Как вы думаете от кого зависит успех нашего урока? (От работы каждого из нас)
Варианты работ учащихся
10. Итог урока (на электрифицированном стенде)
— Сколько у куба вершин? (8)
— Сколько к куба ребёр? (12)
— Как называется правильный шестигранник? (куб)
— Что является гранью куба? (квадрат)
б) Рефлексивно-оценочная деятельность
Оцените свою работу на уроке. (Лесенка успеха)
11. Домашнее задание.
Выполнить задание по карточкам по выбору,
Раскрасить ту фигуру, которая является разверткой куба.
Куб — свойства, виды и формулы
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.