Что такое ребро треугольной пирамиды
Пирамида
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Виды пирамид
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Геометрические фигуры. Пирамида.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые имеют общую вершину. Пирамида – это частный случай конуса.
Элементы пирамиды.
Свойства пирамиды.
1. Когда все боковые ребра имеют одинаковую величину, тогда:
2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:
3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу.
4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.
5. Конус будет вписанным в пирамиду, когда вершины их совпадут, а основание конуса будет вписанным в основание пирамиды. При этом вписать конус в пирамиду можно лишь в том случае, если апофемы пирамиды имеют равные величины (необходимое и достаточное условие).
6. Конус будет описанным около пирамиды, если их вершины совпадут, а основание конуса будет описано около основания пирамиды. При этом описать конус около пирамиды можно лишь в том случае, если все боковые ребра пирамиды имеют одинаковые величины (необходимое и достаточное условие). Высоты у этих конусов и пирамид одинаковы.
7. Цилиндр будет вписанным в пирамиду, если 1-но его основание совпадет с окружностью, которая вписана в сечение пирамиды плоскостью, параллельной основанию, а второе основание будет принадлежать основанию пирамиды.
8. Цилиндр будет описанным около пирамиды, когда вершина пирамиды будет принадлежать его одному основанию, а второе основание цилиндра будет описано около основания пирамиды. При этом описать цилиндр около пирамиды можно лишь в том случае, если основанием пирамиды служит вписанный многоугольник (необходимое и достаточное условие).
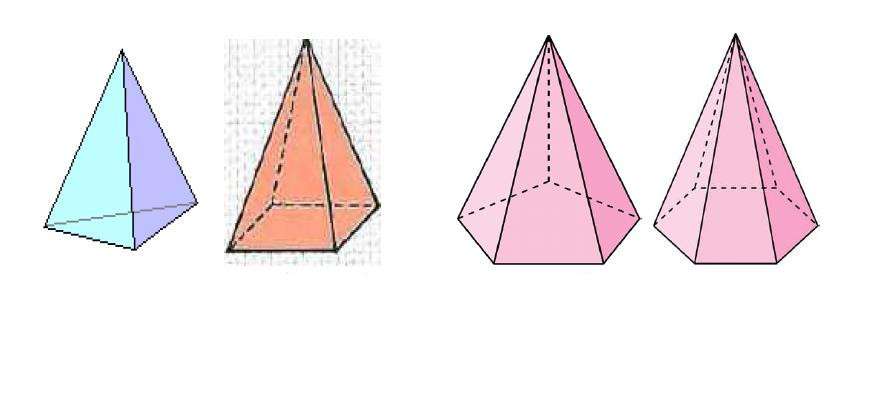
Виды пирамид.
По количеству углов основания пирамиды делят на треугольные, четырехугольные и так далее.
Пирамида будет треугольной, четырехугольной, и так далее, когда основанием пирамиды будет треугольник, четырехугольник и так далее. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и так далее.
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
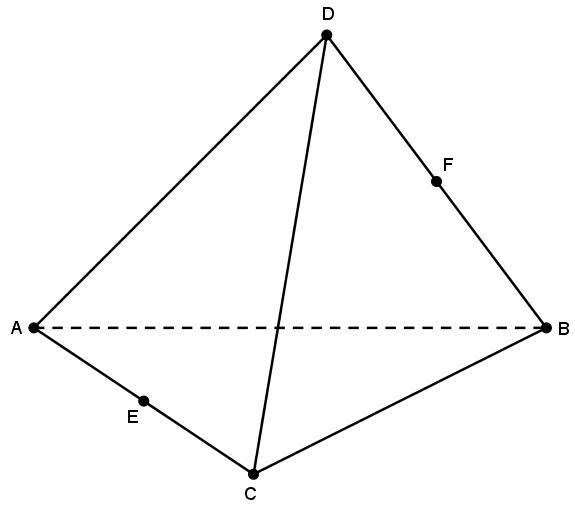
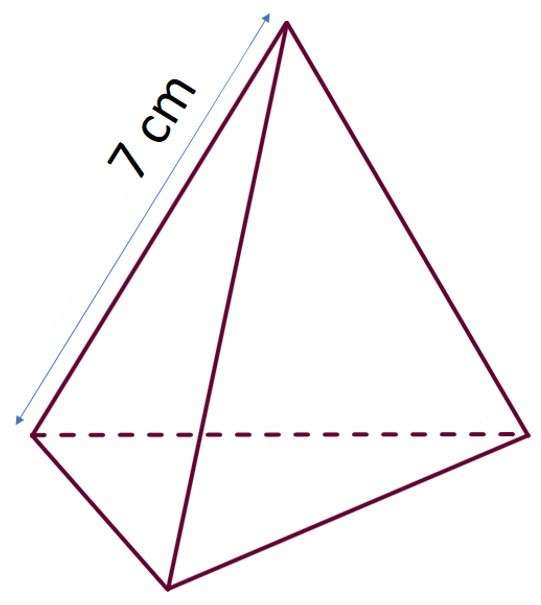
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.
Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
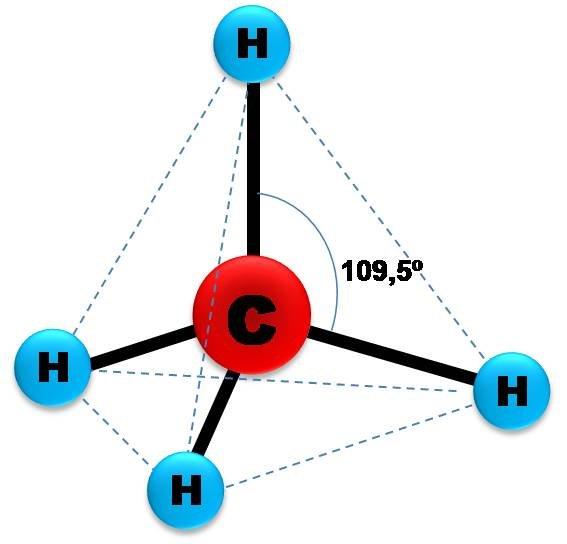
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
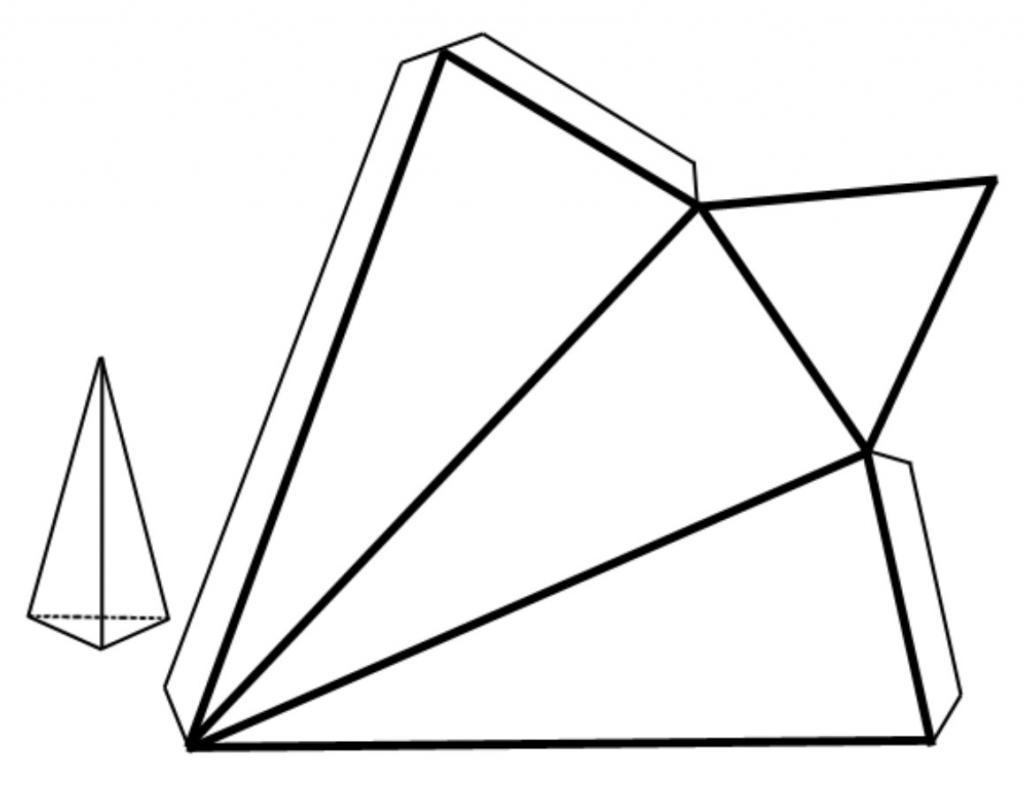
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Пирамида и ее боковые ребра. Формулы. Боковое ребро пирамиды Хеопса
Пирамида как фигура геометрии
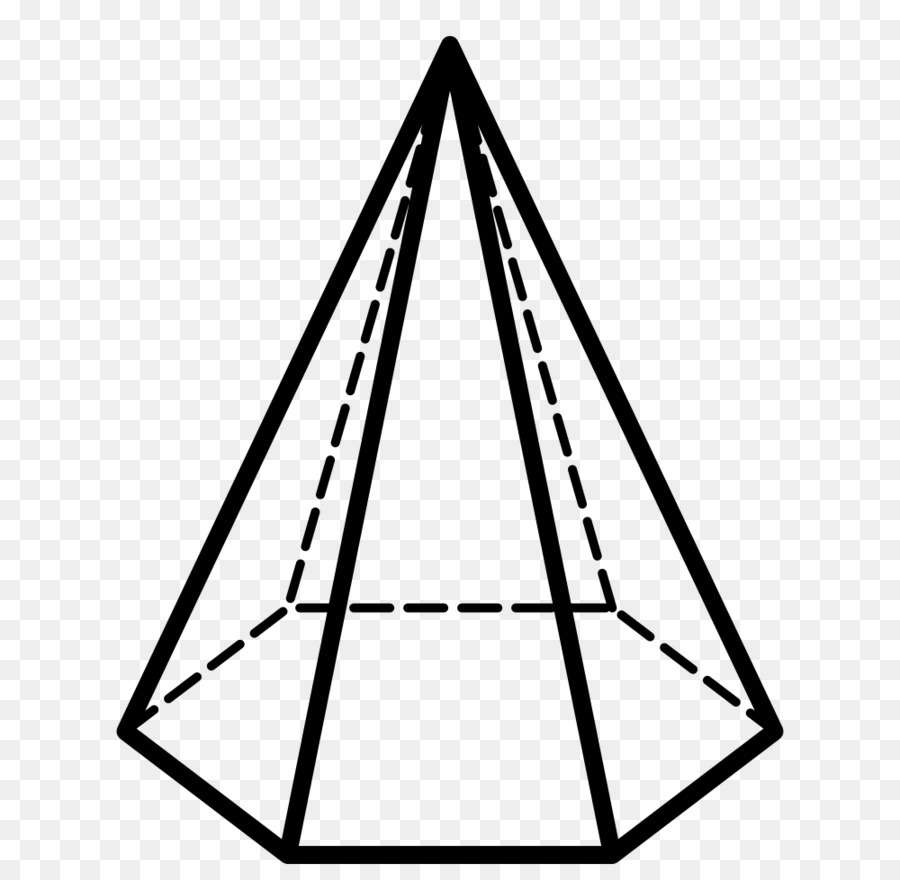
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.

С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Задача на определение бокового ребра пирамиды Хеопса
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).
Геометрические фигуры. Правильная пирамида.
В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.
Правильная пирамида обладает следующими свойствами:
Формулы для правильной пирамиды.
Ниже указанная формула определения объема используется лишь для правильной пирамиды:
Боковое ребро правильной пирамиды находят по формуле:
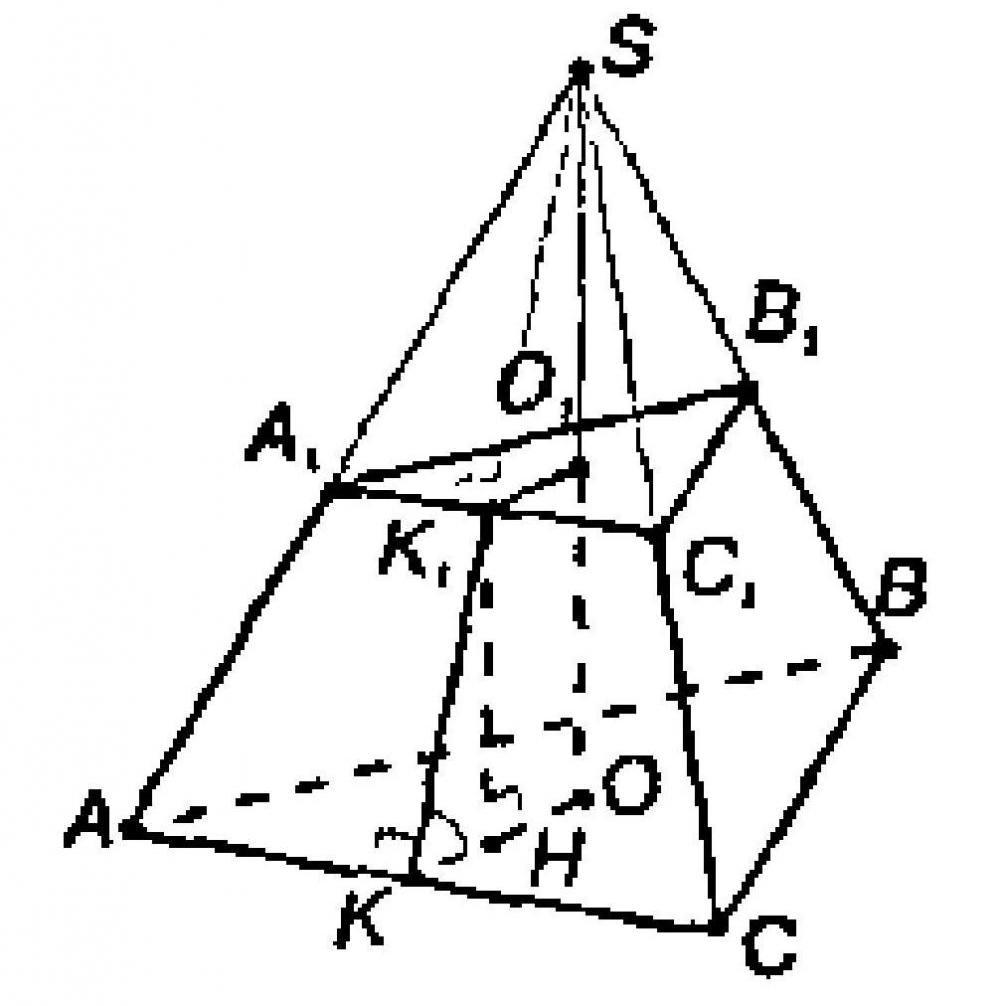
где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Правильная треугольная пирамида.
Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:
Еще одним частным случаем правильно пирамиды является тетраэдр.