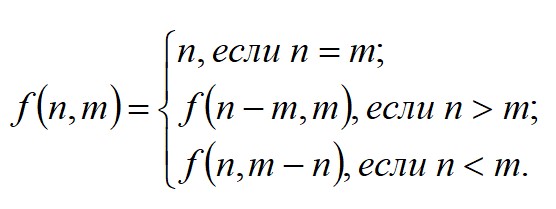Что такое рекурсия недостатки и преимущества
BestProg
Рекурсия. Примеры решения задач. Преимущества и недостатки рекурсии
Содержание
Поиск на других ресурсах:
1. Что такое рекурсия? Что называется рекурсией?
В теории алгоритмов дается следующее определение рекурсии: рекурсия – это такой способ задания функции, при котором результат возврата из функции для данного значения аргумента определяется на основе результата возврата из той же функции для предыдущего (меньшего или большего) значения аргумента.
Другими словами, рекурсия – это вызов функции самой себя для перехода к следующему шагу рекурсии. Чтобы следующий шаг рекурсии отличался от предыдущего, значение как минимум одного из параметров функции должно изменяться в процессе рекурсивного вызова.
2. Объяснение к реализации задач на рекурсию. Как правильно организовать рекурсивный вызов функции?
Рекурсивное обращение к функции может быть осуществлено, если алгоритм определен рекурсивно. Использование рекурсии не всегда бывает эффективным, например, в случаях, где много переменных используются или влияют на количество итераций цикла. Однако, циклы, в которых количество изменяемых величин (итераторов) не очень велико, можно представить рекурсией.
Чтобы циклический процесс превратить в рекурсивный, нужно уметь определить (выделить) три важных момента:
3. Поиск суммы элементов массива. Пример
По подобному примеру можно создавать собственные рекурсивные функции, которые определяют любые суммы элементов любых массивов.
где n – количество элементов массива. Программный код функции следующий:
В вышеприведенном коде функция получает два параметра. Первый параметр i есть значением текущего индекса, который изменяет свое значение при каждом рекурсивном вызове. Второй параметр A – массив, элементы которого суммируются.
Поскольку, осуществляется сумма текущего значения A[i] со следующими, то указывается строка
Использование функции Sum() в другом программном коде может быть следующим:
В примере разработана рекурсивная функция, которая находит факториал заданного числа n
Программный код функции следующий:
При возврате на уровень выше возвращается текущее значение n и результат вычислений при следующих рекурсивных вызовах:
Использование функции в другом программном коде:
5. Программа нахождения наибольшего общего делителя по алгоритму Евклида. Пример
В примере определяется наибольший общий делитель по формуле Евклида:
Программный код функции следующий:
Использование функции MaxDivisor
Последовательность чисел Фибоначчи имеет вид:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
Ниже приведен текст функции GetNFibonacci()
Использование метода GetNFibonacci() в другом программном коде:
7. Преимущества и недостатки использования рекурсии
Рекурсию часто сравнивают с итерацией. Организация циклического процесса с помощью рекурсии имеет свои преимущества и недостатки.
Можно выделить следующие взаимосвязанные преимущества рекурсии:
Недостатки рекурсии состоят в следующем:
Каковы преимущества и недостатки рекурсии?
с уважением, используя рекурсию нерекурсивных методов в алгоритмах сортировки или, если на то пошло, любой алгоритм, каковы его плюсы и минусы?
8 ответов
по большей части рекурсия медленнее и занимает больше места в стеке. Основным преимуществом рекурсии является то, что для таких задач, как обход дерева, она делает алгоритм немного проще или более «элегантным». Проверьте некоторые из сравнений:
рекурсия означает, что функция вызывает повторно
Он использует системный стек для выполнения своей задачи. Как стек использует подход LIFO и когда функция называется контролируемой, перемещается туда, где определена функция, которая хранится в памяти с некоторым адресом, этот адрес хранится в стеке
во-вторых, это снижает сложность программы.
хотя немного не по теме, немного связано. Должны прочитать. : рекурсия против итерации
все алгоритмы могут быть определены рекурсивно. Это значительно облегчает визуализацию и доказательство.
некоторые алгоритмы (например,Функция Аккермана) невозможно (легко) указать итеративно.
рекурсивная реализация будет использовать больше памяти, чем цикл если оптимизация хвостового вызова невозможно выполнить. Хотя итерация может использовать меньше памяти, чем рекурсивная функция, которая не может быть оптимизирована, у нее есть некоторые ограничения выразительная сила.
Я лично предпочитаю использовать итеративную над рекурсивной функцией. Особенно, если ваша функция имеет сложную/тяжелую логику и количество итераций велико. Это потому, что с каждым рекурсивным вызовом стек вызовов увеличивается. Это может привести к сбою стека, если операции слишком велики, а также замедлить процесс.
любой алгоритм, реализованный с помощью рекурсии, также может быть реализован с помощью итерации.
почему не использовать рекурсию
почему to использовать рекурсию
например, проблема Ханойской башни легче решается с помощью рекурсии, а не итерации.
экспрессивность
большинство проблем естественно выражаются рекурсией, такой как Фибоначчи, сортировка слиянием и быстрая сортировка. В этом отношении код написан для людей, а не для машин.
неизменяемости
итеративные решения часто полагаются на различные временные переменные, что затрудняет чтение кода. Этого можно избежать с помощью рекурсии.
производительность
рекурсия не является дружественной к стеку. Стек может переполниться, когда рекурсия плохо спроектирована или оптимизация хвоста не поддерживается.
возникнет ситуация, когда вам придется отказаться от рекурсии в проблеме, где рекурсия, по-видимому, в ваших интересах, это связано с тем, что для проблем, где ваша рекурсия должна была бы произойти тысячу раз, это приведет к ошибке stackoverflow, даже если ваш код не застрял в бесконечной рекурсии. Большинство языков программирования ограничивает вас несколькими вызовами стека, поэтому, если ваша рекурсия выходит за этот предел, вы можете не использовать рекурсия.
BestProg
Рекурсия. Примеры решения задач. Преимущества и недостатки рекурсии
Содержание
Поиск на других ресурсах:
1. Что такое рекурсия? Что называется рекурсией?
Любая функция (метод) в своем теле может вызывать сама себя. Рекурсия – это такой способ определения функции, при котором результат возврата из функции для данного значения аргумента определяется на основе результата возврата из той же функции для предыдущего (меньшего или большего) значения аргумента.
Если функция (метод) вызывает сам себя, то такой вызов называется рекурсивным вызовом функции. При каждом рекурсивном вызове запоминаются предыдущие значения внутренних локальных переменных и полученных параметров функции. Чтобы следующий шаг рекурсивного вызова отличался от предыдущего, значение как-минимум одного из параметров функции должно быть изменено. Остановка процесса рекурсивных вызовов функции происходит, когда изменяемый параметр достиг некоторого конечного значения, например, обработан последний элемент в массиве.
2. Объяснения к реализации задач на рекурсию. Как правильно организовать рекурсивный вызов функции?
Рекурсивное обращение к функции может быть осуществлено, если алгоритм определен рекурсивно.
Чтобы циклический процесс преобразовать в рекурсивный, нужно уметь определить (выделить) три важных момента:
3. Поиск суммы элементов массива. Пример
По подобному примеру можно создавать собственные рекурсивные функции, которые определяют любые суммы элементов любых массивов.
где n – количество элементов массива. Программный код функции следующий:
Как видно из примера, в рекурсивную функцию Sum() передается 3 параметра:
Выход из функции осуществляется, если будет обработан последний элемент массива. Условие прекращения рекурсивного процесса имеет вид:
Для суммирования текущего значения A[i] со следующими указывается строка:
Использование функции Sum() в другом программном коде может быть, например, таким:
4. Пример подсчета количества вхождений заданного символа в строке
Реализация функции Count() следующая:
5. Пример нахождения факториала числа – n!
Вычисление факториала числа методом рекурсии есть почти в каждом учебнике. Факториал числа вычисляется по формуле
Рекурсивный вызов можно организовать двумя способами:
В данном примере разработаны две функции, которые находят факториал обоими способами. Программный код функций следующий:
Использование функций в другом программном коде может быть следующим:
6. Программа нахождения наибольшего общего делителя (алгоритм Евклида). Пример
В примере определяется наибольший общий делитель по формуле Евклида:
Программный код функции следующий:
Использование функции MaxDiv() может быть следующим:
7. Подсчет количества элементов массива, больших заданного числа. Пример
Использование метода Count() в другом методе
8. Преимущества использования рекурсии в программах. Пример
Рекурсию часто сравнивают с итерацией. Организация циклического процесса с помощью рекурсии имеет свои преимущества и недостатки.
Можно выделить следующие взаимосвязанные преимущества рекурсии:
Недостатки рекурсии состоят в следующем:
Каковы преимущества и недостатки рекурсии?
Что касается использования рекурсии над нерекурсивными методами в алгоритмах сортировки или, в этом отношении, любого алгоритма, каковы его плюсы и минусы?
Рекурсия означает, что функция вызывает несколько раз
Он использует системный стек для выполнения своей задачи. Поскольку в стеке используется подход LIFO И когда вызывается функция, управляемая перемещается туда, где определена функция, которая хранится в памяти с некоторым адресом, этот адрес хранится в стеке.
Во-вторых, это уменьшает временную сложность программы.
Хотя немного не по теме, немного связано. Должен прочитать. : Рекурсия против итерации
Все алгоритмы могут быть определены рекурсивно. Это значительно упрощает визуализацию и доказательство.
Некоторые алгоритмы (например, функция Аккермана ) не могут (легко) быть определены итеративно.
Рекурсивная реализация будет использовать больше памяти, чем цикл, если оптимизация хвостового вызова не может быть выполнена. Хотя итерация может использовать меньше памяти, чем рекурсивная функция, которая не может быть оптимизирована, она имеет некоторые ограничения в своей выразительной силе.
Я лично предпочитаю использовать Iterative по сравнению с рекурсивной функцией. Особенно, если ваша функция имеет сложную/тяжелую логику и количество итераций велико. Это потому, что с каждым рекурсивным стеком вызовов увеличивается. Это может привести к краху стека, если ваши операции слишком велики, а также замедлить процесс.
Любой алгоритм, реализованный с использованием рекурсии, также может быть реализован с использованием итерации.
Почему нет использовать рекурсию
Почему для использовать рекурсию
Например, проблема Ханойской башни легче решить с помощью рекурсии, а не итерации.
Выразительность
Большинство проблем естественным образом выражается в рекурсии, такой как Фибоначчи, сортировка слиянием и быстрая сортировка. В этом отношении код написан для людей, а не для машин.
Неизменность
Итеративные решения часто зависят от изменяющихся временных переменных, что затрудняет чтение кода. Этого можно избежать с помощью рекурсии.
Спектакль
Рекурсия не подходит для стека. Стек может переполниться, если рекурсия не разработана должным образом или оптимизация хвоста не поддерживается.
Может возникнуть ситуация, когда вам придется отказаться от рекурсии в проблеме, в которой рекурсия кажется вам выгодной, это связано с тем, что для проблем, когда ваша рекурсия должна происходить тысячи раз, это может привести к ошибке stackoverflow, даже если ваш код это сделал не застрять в бесконечной рекурсии. Большинство языков программирования ограничивают вас количеством вызовов стека, поэтому, если ваша рекурсия выходит за пределы этого предела, вы можете не использовать рекурсию.
Мы должны использовать рекурсию в следующих сценариях:
Рекурсия спасет несколько обходов. И это будет полезно, если мы сможем разделить распределение стека следующим образом:
В этом случае только половина стеков будет выделено в любой момент времени.
Каковы преимущества и недостатки рекурсии?
Что касается использования рекурсии по нерекурсивным методам в алгоритмах сортировки или, если на то пошло, любого алгоритма, каковы его плюсы и минусы?
ОТВЕТЫ
Ответ 1
По большей части рекурсия медленнее и занимает больше стека. Основным преимуществом рекурсии является то, что для таких проблем, как обход дерева, он делает алгоритм немного проще или более «изящным». Проверьте некоторые из сравнений:
Ответ 2
Рекурсия означает повторную вызов функции
Он использует системный стек для выполнения этой задачи. Поскольку стек использует подход LIFO и когда функция называется управляемой, она перемещается туда, где определена функция, которая хранится в памяти с некоторым адресом, этот адрес хранится в стеке
Во-вторых, это уменьшает временную сложность программы.
Хотя бит не по теме, немного связан. Должен прочитать.: Рекурсия против итерации
Ответ 3
Все алгоритмы могут быть определены рекурсивно. Это значительно облегчает визуализацию и доказательство.
Некоторые алгоритмы (например, Ackermann Function) не могут (легко) быть указаны итеративно.
Рекурсивная реализация будет использовать больше памяти, чем цикл, если оптимизация хвостовых вызовов не может быть выполнена. Хотя итерация может использовать меньше памяти, чем рекурсивная функция, которая не может быть оптимизирована, она имеет некоторые ограничения в ее выразительной мощности.
Ответ 4
Я лично предпочитаю использовать итеративную над рекурсивной функцией. Особенно, если вы работаете с сложной/тяжелой логикой, и количество итераций велико. Это связано с тем, что с каждым рекурсивным вызовом стек вызовов увеличивается. Это может привести к сбою стека, если вы слишком велики, а также замедлите процесс.
Ответ 5
Ответ 6
Любой алгоритм, реализованный с использованием рекурсии, также может быть реализован с использованием итерации.
Почему бы не использовать рекурсию
Зачем использовать рекурсию
Например, проблему Башни Ханоя легче решать с помощью рекурсии, а не итерации.
Ответ 7
выразительность
Большинство проблем естественно выражается рекурсией, такой как Fibonacci, сортировка слияний и быстрая сортировка. В этом отношении код написан для людей, а не для машин.
Неизменность
Итерационные решения часто полагаются на переменные временные переменные, которые затрудняют чтение кода. Этого можно избежать при рекурсии.
Производительность
Рекурсия не совместима со стеклом. Stack может переполняться, когда рекурсия плохо разработана или оптимизация хвоста не поддерживается.
Ответ 8
Возникает некоторая ситуация, когда вам придется отказаться от рекурсии в проблеме, где рекурсия представляется вам в ваших интересах, это связано с тем, что для проблем, в которых ваша рекурсия должна произойти тысячи раз, это приведет к ошибке stackoverflow, хотя ваш код не застрял в бесконечной рекурсии. Большинство языков программирования ограничивают количество вызовов стека, поэтому, если ваша рекурсия выходит за пределы этого предела, вы можете не использовать рекурсию.
Ответ 9
Мы должны использовать рекурсию в следующих сценариях:
Рекурсия спасет несколько обходов. И это будет полезно, если мы сможем разделить распределение стека следующим образом:
В этом случае только половина стеков будет выделено в любой момент времени.