Что такое ресайз в дизайне
Ликбез: методы ресайза изображений
Почему изображение, масштабированное с бикубической интерполяцией, выглядит не как в Фотошопе. Почему одна программа ресайзит быстро, а другая — нет, хотя результат одинаковый. Какой метод ресайза лучше для увеличения, а какой для уменьшения. Что делают фильтры и чем они отличаются.
Вообще, это было вступлением к другой статье, но оно затянулось и вылилось в отдельный материал.

Этот человек сидит среди ромашек, чтобы привлечь ваше внимание к статье.
Для наглядного сравнения я буду использовать изображения одинакового разрешения 1920×1280 (одно, второе), которые буду приводить к размерам 330×220, 1067×667 и 4800×3200. Под иллюстрациями будет написано, сколько миллисекунд занял ресайз в то или иное разрешение. Цифры приведены лишь для понимания сложности алгоритма, поэтому конкретное железо или ПО, на котором они получены, не так важно.
Ближайший сосед (Nearest neighbor)
Это самый примитивный и быстрый метод. Для каждого пикселя конечного изображения выбирается один пиксель исходного, наиболее близкий к его положению с учетом масштабирования. Такой метод дает пикселизированное изображение при увеличении и сильно зернистое изображение при уменьшении.
Вообще, качество и производительность любого метода уменьшения можно оценить по отношению количества пикселей, участвовавших в формировании конечного изображения, к числу пикселей в исходном изображении. Чем больше это отношение, тем скорее всего алгоритм качественнее и медленнее. Отношение, равное одному, означает что как минимум каждый пиксель исходного изображения сделал свой вклад в конечное. Но для продвинутых методов оно может быть и больше одного. Дак вот, если например мы уменьшаем изображение методом ближайшего соседа в 3 раза по каждой стороне, то это соотношение равно 1/9. Т.е. большая часть исходных пикселей никак не учитывается.
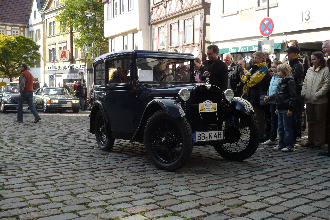
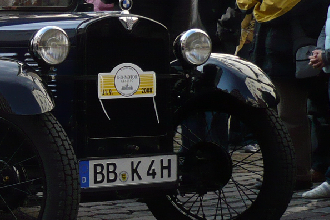

1920×1280 → 330×220 = 0,12 ms
1920×1280 → 1067×667 = 1,86 ms
1920×1280 → 4800×3200 = 22,5 ms
Теоретическая скорость работы зависит только от размеров конечного изображения. На практике при уменьшении свой вклад вносят промахи кеша процессора: чем меньше масштаб, тем меньше данных используется из каждой загруженной в кеш линейки.
Метод осознанно применяется для уменьшения крайне редко, т.к. дает очень плохое качество, хотя и может быть полезен при увеличении. Из-за скорости и простоты реализации он есть во всех библиотеках и приложениях, работающих с графикой.
Аффинные преобразования (Affine transformations)
Аффинные преобразования — общий метод для искажения изображений. Они позволяют за одну операцию повернуть, растянуть и отразить изображение. Поэтому во многих приложениях и библиотеках, реализующих метод аффинных преобразований, функция изменения изображений является просто оберткой, рассчитывающей коэффициенты для преобразования.
Принцип действия заключается в том, что для каждой точки конечного изображения берется фиксированный набор точек исходного и интерполируется в соответствии с их взаимным положением и выбранным фильтром. Количество точек тоже зависит от фильтра. Для билинейной интерполяции берется 2×2 исходных пикселя, для бикубической 4×4. Такой метод дает гладкое изображение при увеличении, но при уменьшении результат очень похож на ближайшего соседа. Смотрите сами: теоретически, при бикубическом фильтре и уменьшении в 3 раза отношение обработанных пикселей к исходным равно 4² / 3² = 1,78. На практике результат значительно хуже т.к. в существующих реализациях окно фильтра и функция интерполяции не масштабируются в соответствии с масштабом изображения, и пиксели ближе к краю окна берутся с отрицательными коэффициентами (в соответствии с функцией), т.е. не вносят полезный вклад в конечное изображение. В результате изображение, уменьшенное с бикубическим фильтром, отличается от изображения, уменьшенного с билинейным, только тем, что оно еще более четкое. Ну а для билинейного фильтра и уменьшения в три раза отношение обработанных пикселей к исходным равно 2² / 3² = 0.44, что принципиально не отличается от ближайшего соседа. Фактически, аффинные преобразования нельзя использовать для уменьшения более чем в 2 раза. И даже при уменьшении до двух раз они дают заметные эффекты лесенки для линий.
Теоретически, должны быть реализации именно аффинных преобразований, масштабирующие окно фильтра и сам фильтр в соответствии с заданными искажениями, но в популярных библиотеках с открытым исходным кодом я таких не встречал.



1920×1280 → 330×220 = 6.13 ms
1920×1280 → 1067×667 = 17.7 ms
1920×1280 → 4800×3200 = 869 ms
Время работы заметно больше, чем у ближайшего соседа, и зависит от размера конечного изображения и размера окна выбранного фильтра. От промахов кеша уже практически не зависит, т.к. исходные пиксели используются как минимум по двое.
Мое скромное мнение, что использование этого способа для произвольного уменьшения изображений попросту является багом, потому что результат получается очень плохой и похож на ближайшего соседа, а ресурсов на этот метод нужно значительно больше. Тем не менее, этот метод нашел широкое применение в программах и библиотеках. Самое удивительное, что этот способ используется во всех браузерах для метода канвы drawImage() (наглядный пример), хотя для простого отображения картинок в элементе используются более аккуратные методы (кроме IE, в нем для обоих случаев используются аффинные преобразования). Помимо этого, такой метод используется в OpenCV, текущей версии питоновской библиотеки Pillow (об этом я надеюсь написать отдельно), в Paint.NET.
Кроме того, именно этот метод используется видеокартами для отрисовки трехмерных сцен. Но разница в том, что видеокарты для каждой текстуры заранее подготавливают набор уменьшенных версий (mip-уровней), и для окончательной отрисовки выбирается уровень с таким разрешением, чтобы уменьшение текстуры было не более двух раз. Кроме этого, для устранения резкого скачка при смене mip-уровня (когда текстурированный объект приближается или отдаляется), используется линейная интерполяция между соседними mip-уровнями (это уже трилинейная фильтрация). Таким образом для отрисовки каждого пикселя трехмерного объекта нужно интерполировать между 2³ пикселями. Это дает приемлемый для быстро движущейся картинки результат за время, линейное относительно конечного разрешения.
Суперсемплинг (Supersampling)
С помощью этого метода создаются те самые mip-уровни, с помощью него (если сильно упростить) работает полноэкранное сглаживание в играх. Его суть в разбиении исходного изображения по сетке пикселей конечного и складывании всех исходных пикселей, приходящихся на каждый пиксель конечного в соответствии с площадью, попавшей под конечный пиксель. При использовании этого метода для увеличения, на каждый пиксель конечного изображения приходится ровно один пиксель исходного. Поэтому результат для увеличения равен ближайшему соседу.
Можно выделить два подвида этого метода: с округлением границ пикселей до ближайшего целого числа пикселей и без. В первом случае алгоритм становится малопригодным для масштабирования меньше чем в 3 раза, потому что на какой-нибудь один конечный пиксель может приходиться один исходный, а на соседний — четыре (2×2), что приводит к диспропорции на локальном уровне. В то же время алгоритм с округлением очевидно можно использовать в случаях, когда размер исходного изображения кратен размеру конечного, или масштаб уменьшения достаточно мал (версии разрешением 330×220 почти не отличаются). Отношение обработанных пикселей к исходным при округлении границ всегда равно единице.



1920×1280 → 330×220 = 7 ms
1920×1280 → 1067×667 = 15 ms
1920×1280 → 4800×3200 = 22,5 ms
Подвид без округления дает отличное качество при уменьшении на любом масштабе, а при увеличении дает странный эффект, когда большая часть исходного пикселя на конечном изображении выглядит однородной, но на краях видно переход. Отношение обработанных пикселей к исходным без округления границ может быть от единицы до четырех, потому что каждый исходный пиксель вносит вклад либо в один конечный, либо в два соседних, либо в четыре соседних пикселя.



1920×1280 → 330×220 = 19 ms
1920×1280 → 1067×667 = 45 ms
1920×1280 → 4800×3200 = 112 ms
Производительность этого метода для уменьшения ниже, чем у аффинных преобразований, потому что в расчете конечного изображения участвуют все пиксели исходного. Версия с округлением до ближайших границ обычно быстрее в несколько раз. Также возможно создать отдельные версии для масштабирования в фиксированное количество раз (например, уменьшение в 2 раза), которые будут еще быстрее.
Данный метод используется в функции gdImageCopyResampled() библиотеки GD, входящей в состав PHP, есть в OpenCV (флаг INTER_AREA), Intel IPP, AMD Framewave. Примерно по такому же принципу работает libjpeg, когда открывает изображения в уменьшенном в несколько раз виде. Последнее позволяет многим приложениям открывать изображения JPEG заранее уменьшенными в несколько раз без особых накладных расходов (на практике libjpeg открывает уменьшенные изображения даже немного быстрее полноразмерных), а затем применять другие методы для ресайза до точных размеров. Например, если нужно отресайзить JPEG разрешением 1920×1280 в разрешение 330×220, можно открыть оригинальное изображение в разрешении 480×320, а затем уменьшить его до нужных 330×220.
Свертки (Convolution)
Этот метод похож на аффинные преобразования тем, что используются фильтры, но имеет не фиксированное окно, а окно, пропорциональное масштабу. Например, если размер окна фильтра равен 6, а размер изображения уменьшается в 2,5 раза, то в формировании каждого пикселя конечного изображения принимает участие (2,5 * 6)² = 225 пикселей, что гораздо больше, чем в случае суперсемплинга (от 9 до 16). К счастью, свертки можно считать в 2 прохода, сначала в одну сторону, потом в другую, поэтому алгоритмическая сложность расчета каждого пикселя равна не 225, а всего (2,5 * 6) * 2 = 30. Вклад каждого исходного пикселя в конечный как раз определяется фильтром. Отношение обработанных пикселей к исходным целиком определяется размером окна фильтра и равно его квадрату. Т.е. для билинейного фильтра это отношение будет 4, для бикубического 16, для Ланцоша 36. Алгоритм прекрасно работает как для уменьшения, так и для увеличения.



1920×1280 → 330×220 = 76 ms
1920×1280 → 1067×667 = 160 ms
1920×1280 → 4800×3200 = 1540 ms
Скорость работы этого метода зависит от всех параметров: размеров исходного изображения, размера конечного изображения, размера окна фильтра.
Именно этот метод реализован в ImageMagick, GIMP, в текущей версии Pillow с флагом ANTIALIAS.
Одно из преимуществ этого метода в том, что фильтры могут задаваться отдельной функцией, никак не привязанной к реализации метода. При этом функция самого фильтра может быть достаточно сложной без особой потери производительности, потому что коэффициенты для всех пикселей в одном столбце и для всех пикселей в одной строке считаются только один раз. Т.е. сама функция фильтра вызывается только (m + n) * w раз, где m и n — размеры конечного изображения, а w — размер окна фильтра. И наклепать этих функций можно множество, было бы математическое обоснование. В ImageMagick, например, их 15. Вот как выглядят самые популярные:
Примечательно, что некоторые фильтры имеют зоны отрицательных коэффициентов (как например бикубический фильтр или фильтр Ланцоша). Это нужно для придания переходам на конечном изображении резкости, которая была на исходном.
Почему важны ресайзы рекламных баннеров в социальных сетях?
Время чтения: 3 минуты Нет времени читать?
В этой статье я хочу рассказать, почему нужно учитывать резайры (изменение размера) изображений в соц. сетях.
Рекомендованные размеры рекламных баннеров социальных сетей важно учитывать, потому что картинки меньше рекомендованного размера «растягиваются» и становятся нечеткими, а картинки большего размера могут «сжиматься» и тоже выглядеть хуже, чем в оригинале, особенно это будет видно на тексте. Если пропорции картинки будут отличаться от рекомендованных, то возможно большая часть изображения будет обрезана и вы потеряете часть нужной информации.
Перед тем, как вы начинаете продумывать рекламную кампанию, вам нужно знать размеры всех креативов, которые будут использоваться в соц. Сетях.
При написании технического задания дизайнеру, нужно обязательно указать все размеры баннеров, которые могут потребоваться.
Также можно, конечно, использовать Photoshop или онлайн сервисы, которые сделают картинку правильного размера.
Размеры изображений Вконтакте
Ниже описаны основные форматы рекламы ВКонтакте, работающие с использованием рекламных баннеров.
1. Изображение и текст (формат 145х85 рх, заголовок в 33 символа и описание в 70).
2. Большое изображение (формат 145х165 рх, текст 33 символа).
3. Продвижение сообществ (формат 145х145 рх, название сообщества).
4. Специальный формат продвижения сообществ (256х256 рх, название сообщества)
Если вы не будите при учитывать эти размеры, то баннер который у вас будет подготовлен может быть обрезан очень сильно.
Первые три формата, показываются пользователям не в ленте, а с левой стороны пользовательского интерфейса ВКонтакте.
Маленький размер этих форматов несколько ограничивает возможности текстового и графического оформления.
При создании рекламной записи с кнопкой либо при размещении в посте ссылки или лидогенерации и загрузке сниппета
1. Изображение нужно загружать 537х240 рх.
На таких изображениях необходимо размещать краткую информацию о рекламируемом продукте и призывы к действию.
У Facebook основные форматы изображения два:
Форматы отображается во всех местах размещения рекламы Facebook. На первый взгляд всё просто, но это не так: чтобы баннер в Facebook показывался и охватывал максимум аудитории, недостаточно просто сделать картинку подходящего формата. Максимальный охват рекламы обеспечат только те изображения, которые содержат не более 20% текста.
При создании баннеров для Instagram с текстом и общим оформлением такая же ситуация, как и в Facebook, нужно обязательно учитывать сколько текста находится на картинке, также изображение, может содержать не более 20%.
Для объявлений в ленте и кольцевой галерее оптимальный размер изображений – 1080х1080 рх, минимально допустимые формат картинок: квадратная – 600х600 рх. Меньший размер изображения не загрузится. Как обычно изображение можно обрезать, но вы можете потерять часть важной информации.
Квадратная форма наиболее приемлема для этой социальной сети. На баннере рекомендуется размещать кнопки с призывом к действию, например, «Узнать больше», «Зарегистрироваться», «Попробовать сейчас». Этот элемент увеличивает кликабельность объявления в Instagram.
Облачный ресайзинг изображений
Привет, мир!
Я являюсь веб разработчиком. В процессе своей профессиональной деятельности мне приходится иметь дело с различными системами и платформами. Как показала практика, не всегда имеется возможность использовать полноценный инвайронмент, необходимый для обработки изображений. Как бы это ни было прискорбно, иногда приходится иметь дело с заказчиками, которые принципиально хостятся на определенной платформе с доисторическим софтом, а иногда, если это образовательное учреждение или еще какая-нибудь составляющая гос.системы, на своих серверах, доступа к которым нет ни у кого.
Задача
Что же делать в таком случае? Кажется возможным не связываться с такими проектами, но не всегда это возможно. Поставим задачу сделать облачную обработку изображений, в частности — ресайз. В рамках одного из условий задачи поставим необходимым ограничения в использовании процессорного времени и установленных графических библиотек на стороне клиента.
Решение
Около года назад у меня возникла необходимость в реалтайм генерации небольших превьюшек картинок фотогалереи на сайте одного образовательного учреждения. В рамках доступной возможности сохранения конфиденциальности не буду упоминать название этого заведения. Так вот, изображения загружаются из админ.панели, и в силу определенной специфики деятельности людей, занимающихся администрированием сайта, не предоставляется возможным принудить их менять размер картинок хотя бы до приемлемого минимума. Т.о. на входе мы имеем картинки размером до 10МБ, на выходе надо отображать их в виде небольшой легковесной галереи. Единственным возможным вариантом представлялась реализация кешируемого прокси сервера, который брал бы на себя всю головную боль ресайзинга изображений. Не долго думая, я сделал решение на NodeJS с использованием графической библиотеки ImageMagick. Это решение доступно для публичного использования по адресу http://thumber.io.
Особенность реализации
Отдельное внимание хочется уделить особенности хранения «кропнутых» картинок с использованием кеша, благодаря которому при повторном запросе уже обработанного изображения сам процессинг не будет запущен. Это позволяет сэкономить время повторной загрузки изображений. Кропнутые изображения хранятся на S3. Инвалидация кешируемого объекта будет произведена только в случае изменения его хеш-суммы или изменения заголовка etag. Для тех, кто не знаком с этим заголовком — https://ru.wikipedia.org/wiki/HTTP_ETag (пардон, если кому-то данная секция может показаться информацией для самых маленьких и тупых).
Примеры
В качестве примера использования могу привести обработку изображения, доступного по адресу
https://habrastorage.org/getpro/habr/comment_images/f22/27f/7d8/f2227f7d86053a207ebc88ae3377af4f.jpg:
Используя наше решение, мы можем сделать его ресайз, чтобы вписать изображение в область размером 200×200, используя следующий урл:
Результат обработки:
Думаю, интуитивно понятно, каким образом можно пользоваться обработкой подобного рода. В качестве параметра после /get/ можно использовать также процентное изменение. Например,
Результат:
Как я сделал самый быстрый ресайз изображений. Часть 1, общие оптимизации
В пилотной части я рассказал о задаче как можно подробнее. Рассказ получился долгим и беспредметным — в нем не было ни одной строчки кода. Но без понимания задачи очень сложно заниматься оптимизацией. Конечно, некоторые техники можно применять, имея на руках только код. Например, кешировать вычисления, сокращать ветвления. Но мне кажется, что некоторые вещи без понимания задачи просто никогда не сделать. Это и отличает человека от оптимизирующего компилятора. Поэтому ручная оптимизация все еще играет огромную роль: у компилятора есть только код, а у человека есть понимание задачи. Компилятор не может принять решение, что значение «4» достаточно случайно, а человек может.
Напомню, что речь пойдет об оптимизации операции ресайза изображения методом сверток в реально существующей библиотеке Pillow. Я буду рассказывать о тех изменениях, что я делал несколько лет назад. Но это не будет повторение слово-в-слово: оптимизации будут описаны в порядке, удобном для повествования. Для этих статей я сделал в репозитории отдельную ветку от версии 2.6.2 — именно с этого момента и будет идти повествование.
Тестирование
Если вы хотите не просто читать, но и экспериментировать самостоятельно, вам пригодится пакет с тестами pillow-perf.
Эти результаты немного отличаются от полученных в официальном бенчмарке для версии 2.6. Тому есть несколько причин:
Структура кода
Как я говорил ранее, ресайз изображения свертками можно сделать в два прохода: на первом меняется только ширина изображения, на втором — высота, или наоборот. Функция ImagingStretch за один вызов как раз может сделать либо то, либо другое. Тут можно увидеть, что она действительно вызывается дважды во время каждого ресайза. В функции выполняется общий пролог, а дальше, в зависимости от параметров, та или иная операция. Довольно необычный подход к избавлению от повторяющегося кода, коим в данном случае является пролог.
Внутри оба прохода выглядят примерно одинаково, с поправкой на меняющееся направление обработки. Для краткости приведу только один:
Тут происходит ветвление на несколько форматов представления пикселей, поддерживаемых Pillow: одноканальные 8 бит (оттенки серого), многоканальные 8 бит (RGB, RGBA, LA, CMYK, некоторые другие), одноканальные 32 бита и float. Нас будет интересовать тело цикла для нескольких каналов по 8 бит, так как это наиболее часто встречающийся формат изображений.
Оптимизация 1: эффективно используем кэш
Хоть я и сказал выше, что два прохода похожи, между ними есть очевидное различие. Посмотрите на вертикальный проход:
На горизонтальный проход:
У вертикального прохода во внутреннем цикле итерируются столбцы конечного изображения, а у горизонтального — строки. Горизонтальный проход представляет серьезную проблему для кеша процессора. На каждом шаге внутреннего цикла происходит обращение на одну строку ниже, а значит запрашивается значение из памяти, лежащее далеко от значения, нужного на предыдущем шаге. Это плохо при небольшом размере свертки. Дело в том, что на современных процессорах линейка кеша, которую процессор может запросить из оперативной памяти, всегда равна 64 байтам. Это значит, что если в свертке участвует меньше 16 пикселей, то часть данных гоняется впустую из оперативной памяти в кеш. А теперь представьте, что циклы поменялись местами и следующий пиксель сворачивается не строкой ниже, а следующий в этой же строке. Тогда большая часть нужных пикселей уже была бы в кеше.
Второй негативный фактор такой организации кода проявляется при длинной строке для свертки (т. е. при сильном уменьшении). Дело в том, что для соседних сверток исходные пиксели довольно значительно пересекаются, и было бы хорошо, если бы эти данные оставались в кеше. Но когда мы движемся сверху вниз, данные для старых сверток постепенно начинают вытесняться из кэша данными для новых. В результате, когда проходит полный внутренний цикл и начинается следующий шаг внешнего, в кеше уже не оказывается верхних строк, они все вытеснены нижними, их нужно снова запрашивать из памяти. А когда дело доходит до нижних, в кеше уже все вытеснено верхними. Получается круговорот, в результате которого в кеше никогда нет нужных данных.
Почему же обход сделан так? В псевдокоде выше видно, что второй строчкой в обоих случаях идет подсчет коэффициентов для свертки. Для вертикального прохода коэффициенты зависят только от строки конечного изображения (от значения yy ), а для горизонтального от текущего столбца (от значения xx ). Т. е. в горизонтальном проходе нельзя просто поменять местами два цикла — расчет коэффициентов должен быть внутри цикла по xx. Если же начать считать коэффициенты внутри внутреннего цикла, это убьёт всю производительность. Особенно когда для расчета коэффициентов применяется фильтр Ланцоша, в котором есть тригонометрические функции.
Вычислять коэффициенты на каждом шаге нельзя, но тем не менее они одинаковые для всех пикселей одного столбца. Значит можно просчитать все коэффициенты заранее для всех столбцов, а во внутреннем цикле брать уже посчитанное. Давайте так и сделаем.
В коде есть выделение памяти для коэффициентов:
Теперь нам понадобится массив таких массивов. Но можно упростить — выделить плоский кусок памяти и эмулировать двумерность адресацией.
Вот теперь можно наконец-то развернуть обход пикселей на 90°:
В четвертом столбце показано ускорение относительно предыдущего варианта, а под таблицей ссылка на коммит, где хорошо видно сделанные изменения.
Оптимизация 2: Ограничение выходных значений
В коде мы в нескольких местах видим такую конструкцию:
Это ограничение значения пикселя в рамках [0, 255], если результат вычислений выходит за пределы 8 бит. Действительно, сумма всех положительных коэффициентов свертки может быть больше единицы, а сумма всех отрицательных может быть меньше нуля. А значит при определенных исходном изображении можем получить переполнение. Это переполнение является результатом компенсации резких перепадов яркости и не является ошибкой.
Это тоже дает прирост производительности, хоть и небольшой.
Как можно заметить, эта оптимизация дала больший эффект для фильтров с меньшим окном и с большим выходным разрешением (единственное исключение это 320×200 Bilinear, но я не берусь сказать, почему). И действительно, чем меньше окно фильтра и больше конечное разрешение, тем больший вклад в производительность делает обрезание значений, которое мы и оптимизировали.
Оптимизация 3: Разворот циклов c постоянным количеством итераций
Если еще раз присмотреться к горизонтальному шагу, там можно насчитать целых 4 вложенных цикла:
Можно на этом не останавливаться и переместить ветвление еще на один уровень выше, до цикла по xx:
Что-то похожее можно сделать и для вертикального прохода. Там сейчас такой код:
Тут нет отдельного итерирования по каналам, вместо этого xx итерируется по ширине, умноженной на 4. Т. е. xx проходится по каждому каналу вне зависимости от их количества в изображении. FIXME в комментарии как раз говорит о том, что это нужно исправить. Исправляется точно так же — ветвлением кода для разного количества каналов в исходном изображении. Приводить код здесь не буду, ссылка на коммит ниже.
Как можно заметить, горизонтальный проход дал больше производительности для уменьшения картинки, тогда как вертикальный — для увеличения.
Оптимизация 4: Целочисленные счетчики
Финал первого акта и босс
Признаюсь, я был очень рад полученным результатам. Удалось разогнать код в среднем в 2,5 раза. Причем для получения этого ускорения пользователю библиотеки не нужно было ставить дополнительное оборудование, ресайз как и раньше идет на одном ядре того же процессора, что и до этого. Нужно было только обновить версию Pillow до версии 2.7.
Но до релиза 2.7 оставалось еще какое-то время, а мне не терпелось проверить новый код на том сервере, на котором он должен был работать. Я перенес код, скомпилировал и сначала подумал, что что-то напутал:
Результат для коммита 57e8925. Получен на другой машине и не участвует в сравнении.
Лолчто? Результаты почти такие же, как до оптимизации. Я 10 раз все перепроверил, поставил принтов, чтобы убедиться, что работает нужный код. Это не был какой-то сайд-эффект от Pillow или окружения, разница воспроизводилась даже на минимальном примере в 30 строчек. Я задал вопрос на Stack Overflow, и в конце концов удалось найти явную закономерность: код выполнялся медленно, если был скомпилирован с GCC под платформу 64 бита. И именно в этом было различие локальной Убунты и на сервере: локально была 32-битная.
Ну слава Муру, я не сошел с ума, это реальный баг в компиляторе. Причем баг был исправлен в GCC 4.9, но GCC 4.8 входил в актуальную на тот момент Ubuntu 14.04 LTS, т. е. скорее всего был установлен у большинства пользователей библиотеки. Игнорировать это было нельзя: что толку от оптимизации, если она не работает у большинства, в том числе и на продакшене, для которого она делалась. Я обновил вопрос на SO и кинул клич в твитере. На него пришел Вячеслав Егоров, один из разработчиков движка V8 и гений оптимизации, который помог докопаться до сути и нашел решение.
Чтобы понять суть проблемы, нужно углубиться в историю процессоров и их текущую архитектуру. Когда-то давно процессоры x86 не умели работать с числами с плавающей точкой, для них был придуман сопроцессор с набором команд x87. Он исполнял инструкции из того же потока, что и центральный процессор, но устанавливался на материнскую плату как отдельное устройство. Довольно быстро сопроцессор стали встраивать в центральный, и физически это стало одним устройством. Долго ли коротко ли, в третьем Пентиуме появился набор инструкций SSE (Streaming SIMD Extensions). Кстати, про SIMD инструкции будет вторая часть цикла статей. Несмотря на название, SSE содержал не только SIMD-команды для работы с числами с плавающей точкой, но и их эквиваленты для скалярных вычислений. Т. е. SSE содержал набор инструкций, дублирующий набор x87, но закодированный иначе и с немного отличающимся поведением.
Тем не менее, компиляторы не спешили генерировать SSE-код для вычислений с плавающей точкой, а продолжали использовать устаревший набор x87. Ведь наличие SSE в процессоре никто не гарантировал, в отличие от x87, который был встроен с незапамятных времен. Все изменилось с приходом 64-битного режима работы процессора. В 64-битом режиме стало обязательным наличие набора инструкций SSE2. Т. е. если вы пишете 64-битную программу для x86, вам доступны как минимум инструкции SSE2. Чем и пользуются компиляторы, генерируя для вычислений с плавающей точкой в 64-битном режиме SSE-инструкции. Напомню, что это никак не связано с векторизацией, речь об обычных скалярных вычислениях.
Именно это и происходит в нашем случае: используются разные наборы инструкций для 32-битного и 64-битного режима. Но пока это не объясняет, почему более современный SSE-код оказывается в разы медленнее устаревшего набора x87. Для объяснения этого феномена нужно разобраться, как именно процессор выполняет инструкции.
Когда-то процессоры действительно «выполняли» инструкции. Они брали инструкцию, декодировали, выполняли её полностью, клали результат куда сказано. Процессоры были довольно тупы. Современные процессоры намного умнее и сложнее, они состоят из десятков разных подсистем. Даже на одном ядре, без всякой параллельной обработки, процессор в один момент времени, в один такт, выполняет несколько инструкций. Просто выполнение происходит на разных стадиях: какая-то инструкция еще только декодируется, какая-то запрашивает что-то из кеша, какая-то передана в арифметический блок. Каждая подсистема процессора занимается своей частью. Это и называется конвейер.
На картинке разные подсистемы обозначены разным цветом. Видно, что хотя команды требует от 4 до 5 тактов на выполнение, благодаря конвейеру каждый такт выбирается одна новая команда и одна завершает свое выполнение.
Конвейер работает тем эффективнее, чем равномернее он заполнен и чем меньше подсистем простаивает. В процессоре даже есть подсистемы, которые планируют оптимальное заполнение конвейера: меняют местами инструкции, дробят одну инструкцию на несколько, объединяют несколько в одну.
Одна из вещей, которая способна заставить конвейер работать не оптимально — зависимость по данным. Это когда для выполнения какой-то инструкции необходим результат выполнения другой инструкции и многие подсистемы простаивают, ожидая когда будет выполнена предыдущая инструкция.
На рисунке видно, что инструкция 2 ждет завершения выполнения инструкции 1. В это время большинство подсистем простаивает. Выполнение всей цепочки команд замедлилось на три такта.
А теперь, вооружившись всеми этими знаниями, давайте посмотрим на псевдокод инструкции, конвертирующей целое число в число с плавающей точкой:
К сожалению, фикс для GCC 4.8 достаточно уродливый, он состоит из ассемблерной вставки и кода препроцессора, который проверяет уместность фикса. Приводить его не буду, ссылки на коммит, как обычно, под результатами тестов. Фикс полностью излечивает 64-битный код.
Результат для коммита 81fc88e. Получен на другой машине и не участвует в сравнении.
Ситуация, описанная тут, совсем не редка. Код, который переводит целые числа в числа с плавающей точкой, а потом производит достаточно небольшие вычисления, встречается почти в каждой программе. Тот же ImageMagick тоже подвержен этой проблеме: 64-битные версии, скомпилированные GCC 4.9 примерно на 40% быстрее скомпилированных более ранними версиями компилятора. Как по мне, это довольно серьезный прокол в системе команд SSE.

















