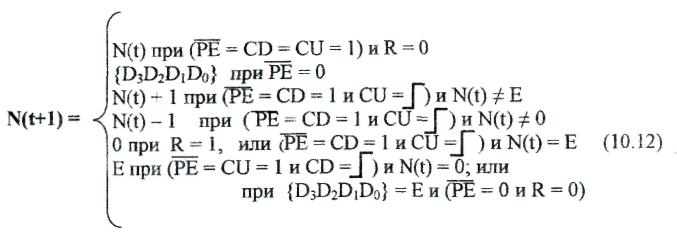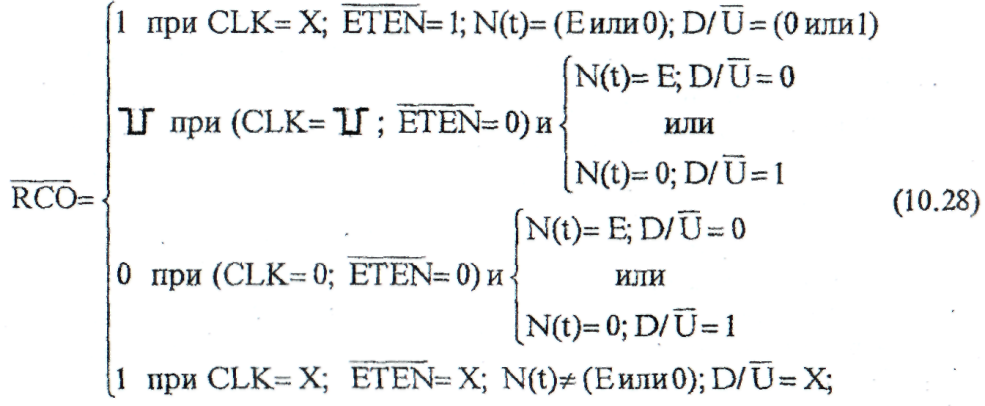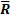Что такое реверсивный счетчик

Реверсивный счётчик, принцип работы.

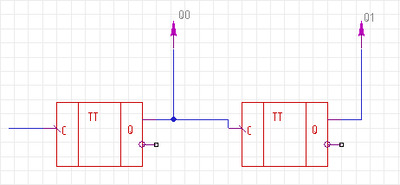
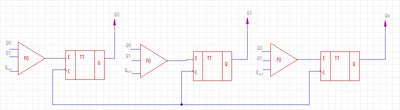
Реверсивный счётчик с последовательным переносом

Реверсивные счетчики могут работать как в режиме сложения, так и в режиме вычитания. Если за период времени T поступит К импульсов при работе счетчика в режиме суммирования и N импульсов при работе счетчика в режиме вычитания, то состояние счетчика будет равно K-N ( при условии, что число импульсов K и N может однозначно подсчитываться счетчиком). Число K-N может быть как положительным, так и отрицательным.

В режиме вычитания входные импульсы подаются на вход «-1», при этом на вход «+1» подаётся лог. 0. В режиме сложения входные импульсы подаются на вход «+1», а на вход «-1» следует подать лог. 0.

Описанные выше счетчики однонаправленные и считают на увеличение, однако на практике часто необходимо менять направление счета в процессе работы. Счетчики, которые в процессе работы могут менять направление счета называются реверсивными.

Первый эксперимент касается оценки частотных, заметьте не нелинейных, а частотных, искажений, возникающих в усилителе с помощью генератора прямоугольных импульсов.

Посмотрим, как реагируют на прохождение прямоугольных импульсов разные электрические RC цепи (это же относится и к LC, и к LR, и к LCR цепям).

Для этого в программе Qucs мы будем пользоваться источником прямоугольных импульсов и такими компонентами, как резисторы, конденсаторы и индуктивности. Если в вашем арсенале приборов есть осциллограф, генератор прямоугольных импульсов или функциональный генератор, то было бы очень полезно повторить эти простые опыты на макетной плате.

На рисунке представлена обычная интегрирующая RC цепочка из резистора R1 и конденсатора C1. Сопротивление R2 — это сопротивление нагрузки, скажем, входное сопротивление осциллографа. Когда мы говорили о частотных свойствах усилителей, рассматривалиамплитудно-частотныехарактеристики каскадов усилителя, то каждый из них можно было рассматривать как идеальный, нечастотно-зависимыйусилитель, к которому добавляется подобная эквивалентная RC цепь.

Для решения различных измерительных задач, для исследования импульсных характеристик микросхем и электронных приборов, для испытаний логических схем и устройств требуются источники электрических сигналов со строго определенными параметрами. Наиболее широко применяются импульсные генераторы, которые выдают видеоимпульсы прямоугольной формы в широком временном, частотном и амплитудном диапазонах: от долей наносекунд до единиц секунд, от долей герц до сотен мегагерц, от долей милливольт до десятков вольт.

Элементы формы реального прямоугольного импульса определены стандартом (рис. 2.5).

Рис.2.5 – Параметры прямоугольного импульсного сигнала.

Искажения формы сигнала связаны с ограничением полосы пропускания канала У. Ограничение со стороны низких частот влекут за собой осцилляции и спад на вершине. Ограничение со стороны высоких частот вызывает увеличение t_ф и t_ср, и появление выбросов на плоской части импульса.

При исследовании импульсных сигналов большое значение приобретает переходная характеристика осциллографа, которая представляет собой изображение единичного скачка напряжения (рис. 2.6).

Рис. 2.6 – Переходная характеристика осциллографа.

Параметром является время нарастания t_н – интервал времени, в течение которого луч проходит путь от уровня 0,1 до уровня 0,9 от установившегося значения. Если плоская часть переходной характеристики имеет выброс d или осцилляции, то используется дополнительный параметр t_у – время установления, отсчитываемое от момента уровня сигнала 0,1 до момента уменьшения осцилляций до заданного уровня.

При измерении параметров прямоугольных импульсов длительность фронта включает в себя время нарастания переходной характеристики. Когда они соизмеримы, время нарастания необходимо исключить.

При длительности фронта, во много раз превышающей время нарастания переходной характеристики, на изображении импульса никаких выбросов не наблюдается.

Генера́тор (лат. generator «производитель») — устройство, производящее какие-либо продукты, вырабатывающее электроэнергию или преобразующее один вид энергии в другой.

Основными динамическими параметрами, представленными на осциллограмме рис. 12.13, являются:

время задержки включения ИС t 1,0зд

время задержки выключения ИС t 0,1зд

время задержки распространения сигнала при включении ИС t 0,1 зд р

время задержки распространения сигнала при выключении ИС t 1,0 зд р

Измерение передаточной характеристики. Передаточную характеристику элемента И можно получить, как показано на рис. 12.14. Напряжение от генератора линейно изменяющегося напряжения 61 подается на ИС и на Х-пластины ЭЛТ. На вертикально отклоняющие пластины подается напряжение с выхода устройства. По получающейся на экране характеристике можно определить:

выходные напряжения логического нуля U°вых и логической единицы U 1 вых, рабочие точки типовых режимов U1 и U2; пороговые напряжения; ширину активной области; запас статической помехоустойчивости; необходимые напряжения сигналов, переводящие схему из состояния нуля в единицу и наоборот.

Измерение выходной характеристики интегральной микросхемы.

Входное напряжение (рис. 12.15) изменяется от значения логического нуля до значения логической единицы, при этом определяют I 0 вх и I 1 вх

Коэффициент разветвления по выходу, определяющий возможность использования данной ИС в комплексе с другими, т. е. их нагрузочную, способность, может быть определен по данным Iвх и Iвых:

I = I 0 вых/I 0 вх, К = I’вых/I 1 вх

Из значений К 0 и К 1 выбирается минимальное.

Измерение динамических параметров цифровых интегральных микросхем.

Причины ложных срабатываний логических элементов

Рассмотрим логическую конструкцию Y = .

При построении этой функции на элементах И-НЕ ее необходимо преобразовать, представив в виде инверсии конъюнкций.

Y =

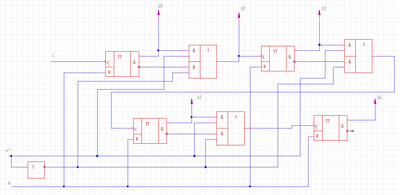
Схема, реализующая эту функцию, показана рис. 1.31.

Рис. 1.31 Схема прохождения сигнала двумя путями

Диаграмма переключений приведена на рис. 1.32.

Рис. 1. 32 Диаграмма переключения схемы (рис. 1.31)

Пусть входной сигнал перешел от «0» к «1». В момент сигнал достигнет порогового уровня и начнется переключение элемента DD1. Сигнал на его выходе станет в момент , отстоящий от на . Поэтому в течение времени на входы DD2 поступают сигналы, превышающие , то есть соответствующие логическим единицам. Следовательно, DD2 одновременно с DD1 начнет переключаться с 1 на 0. В момент создадутся условия для обратного переключения элемента DD2. Через время на выходе уровень напряжения достигнет , следовательно на выходе устройства восстановится логическая «1».

Из диаграммы видно, что за время единичный уровень на выходе изменился на нулевой, то есть правильность выполнения логической операции нарушилась, так как на выходе Y = всегда должна быть логическая «1». Это явление получило название «состязаний» или «гонок».

В триггерах также возможны «состязания» между внешними сигналами и сигналами обратной связи. Устранения ошибок от ложных срабатываний в логических цепях можно добиться путем временного разделения сигналов, исключающих подобные явления. Вырабатываемое логическим устройством напряжение в этом случае передается на последующие устройства не непрерывно и не в произвольные моменты времени, а только в такие моменты, когда искажение правильных значений выходного сигнала за счет «состязаний» заведомо исключено.

Конъюнкция

Это отражает аналогию с арифметическим умножением: умножение любого числа и набора чисел на 0 в результате вернёт всегда 0. Эта логическая операция коммутативна: порядок, в котором она получает входные параметры, никак не повлияет на конечный результат вычисления. Другим свойством этой функции является ассоциативность, или сочетательность. Это свойство позволяет при вычислении последовательности бинарных операций не учитывать порядок вычисления. Поэтому для 3 и более последовательных операций логического умножения нет необходимости учитывать скобки. В программировании эта функция используется зачастую для того, чтобы убедиться в том, что специфические команды выполнятся только при выполнении совокупности определённых условий. Дизъюнкция

Источник

Счетчики (суммирующие, вычитающие и реверсивные): принципы построения и работа счетчиков, счетчики с произвольным коэффициентом пересчета

Содержание

Классификация

Счетчики классифицируются по следующим параметрам:

по типу формирования переноса внутри счетчика

Последовательные суммирующие счетчики

Счетчики с последовательным переносом

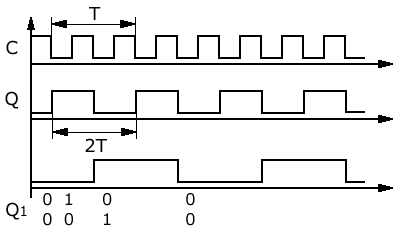
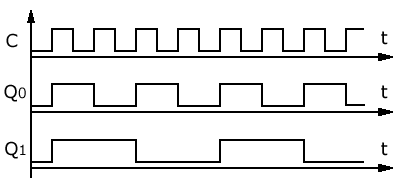
Рис.2 Временные диаграммы

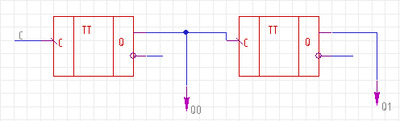
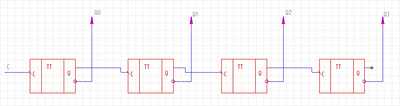
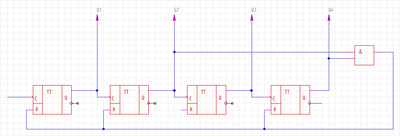
Рис.3 Суммирующий счетчик с последовательным переносом

Счетчики с параллельным переносом

Рис.4 Суммирующий счетчик с параллельным переносом

Счетчики с комбинированным переносом

Последовательные вычитающие счетчики

Рис.5 Вычитающий счетчик

Рис.6 Временные диаграммы вычитающего счетчика

Переключение i-ого разряда осуществляется тогда, когда все разряды от 0-ого до (i-1)-ого равны нулю.

Рис.7 Вычитающий счетчик

Сигнал снимается с инверсного выхода.

Реверсивные счетчики

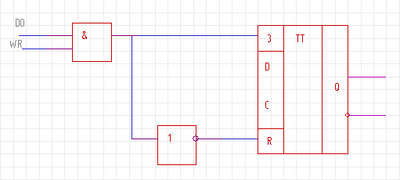
Реверсивный счетчик складывает(по фронту) и вычитает(по спаду) одновременно. Для сброса в нулевое состояние используется универсальный триггер.

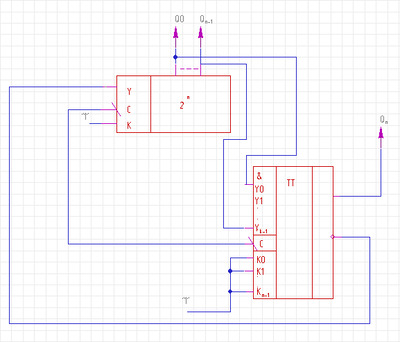
Рис.8 Реверсивный счетчик

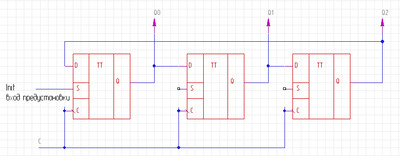
Схема счетчика с предустановкой

Рис.9 Счетчик с сигналом предустановки

Построение счетчиков с произвольным модулем пересчета

Рис.10 Счетчик, считающий по mod10

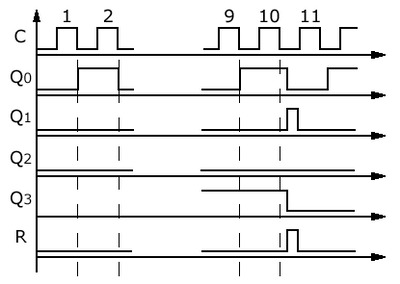
Рис.11 Временные диаграммы

Кольцевые счетчики

Рис.12 Кольцевой счетчик, считающий по mod3

Счетчики на JK-триггерах

Добавление дополнительных состояний

Рис. 13 Добавление нового состояния

С приходом n-ого импульса счетчик переключается в 0, а добавленный триггер в 1. С приходом следующего импульса счетчик не переключается, а добавленный триггер

Счетчики с произвольным порядком пересчета

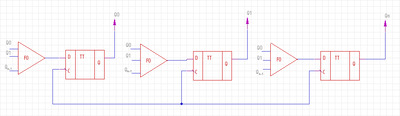
Построенные на основе D-триггеров

Рис.14 Структурная схема

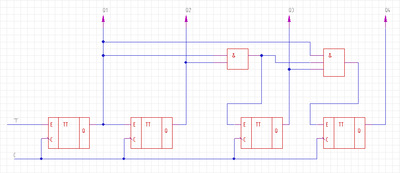
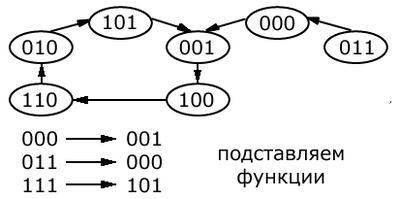
Рис.15 Счетчик с произвольным порядком пересчета и его граф состояний

Рис.16 Граф состояний

Каждый разряд булевой функции определяет значение счетчика.

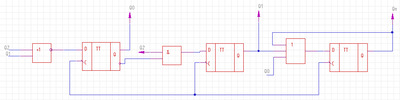
Построенные на основе T-триггеров

Рис.17 Структурная схема

Рис.18 Счетчик с произвольным порядком пересчета

Источник

Реверсивные двоичные счетчики

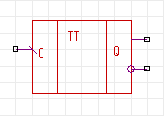
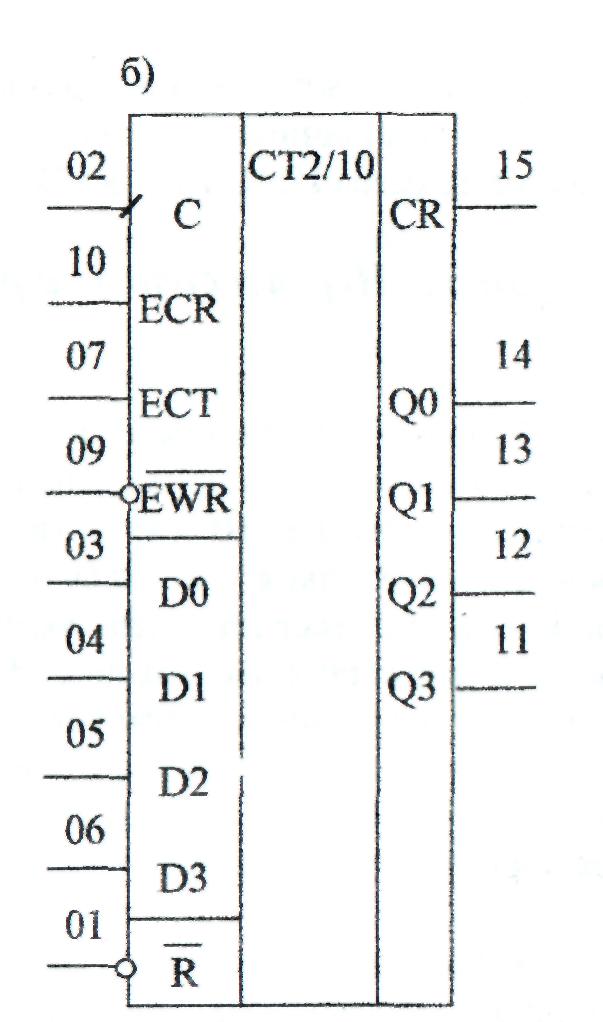
Промышленность выпускает две основные разновидности реверсив­ных двоичных счетчиков, условное графическое обозначение которых представлено на рис. 10.7(a) и (б).

В соответствии с изложенным выше алгоритм управления работой счетчика рис. 10.7(a) может быть представлен следующей системой урав­нений:

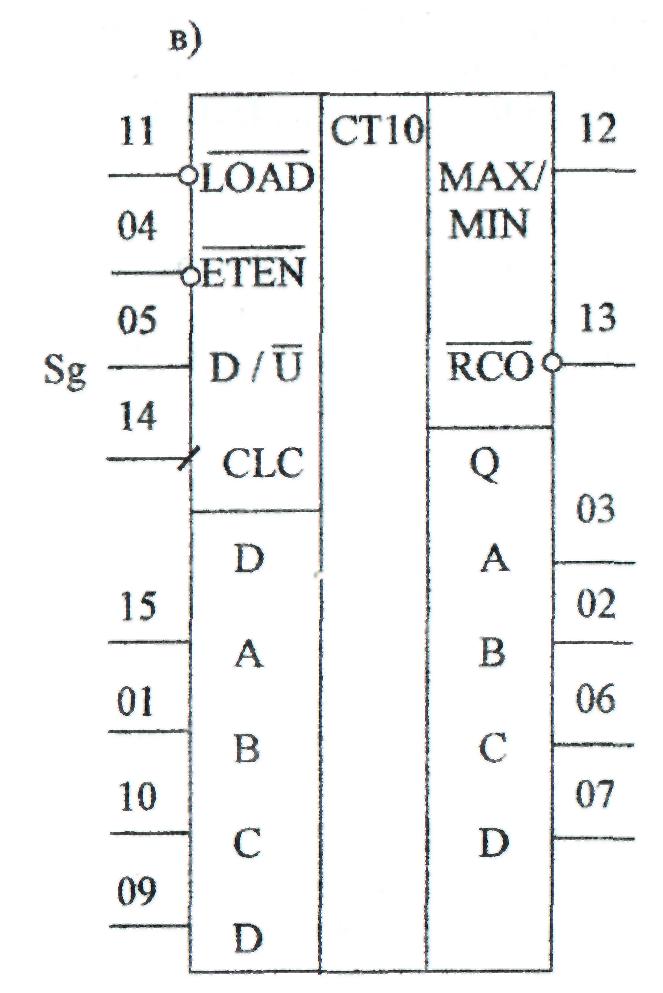
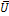
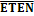
Вторая из указанных разновидностей реверсивных двоичных счетчи­ков (рис. 10.7.б) содержит вход D/ . выбора направления счета, вход раз­решения счета , вход тактирования CLC и вход стробирования предварительной записи .Управление работой счетчиков данной разновидности осуществляется подачей сигналов на указанные входы управления в соответствии со следующей системой уравнений:

В счетчиках рис. 10.7(б) прямой счет осуществляется при низком уров­не напряжения на входе выбора направления счета а обратный – при высоком уровне напряжения на этом входе. При этом на входе разрешения счета ETEN должен быть установлен низкий уровень напряжения, вследст­вие чего срабатывание счетчика будет происходить по положительному фронту тактового импульса на входе CLC. Асинхронная установка счетчи­ка в состояние, заданное на входах A,B,C,Dпроизводится при подаче низ­кого уровня напряжения на входе разрешения предустановки .

Из числа выпускаемых промышленностью интегральных микросхем реверсивных двоичных счетчиков второй разновидности можно привести в качестве примера ИМС типа К555 ИЕ13, КР1533 ИЕ13.

10.5.3. Нереверсивные и реверсивные двоично-десятичные

счетчики

• При параллельной загрузке в счетчик рис. 10.8(б) кода числа > его работа будет развиваться в соответствии с той частью графа переходов рис.10.3, которая относится к его вершинам 10, 11, 12, 13, 14, 15со втекающими в них и вытекающими из них ориентированными дугами ребер графа.

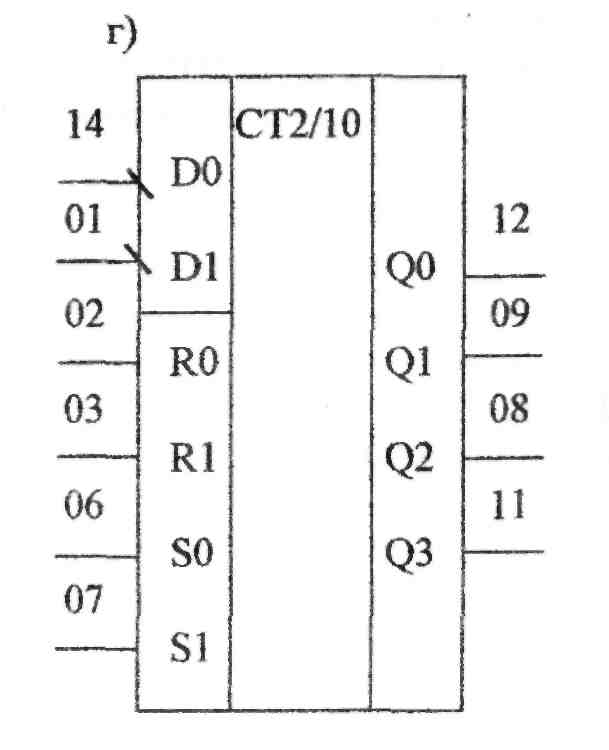
Рис. 10.8. Условное графическое обозначение двоично-десятичных счетчиков.

первой секции счетчика на вход D₁ второй трехразрядной секции счетчика. Алгоритм управления работой десятичного счетчика рис.10.8(г) может быть описан следующей системой уравнений:

В системе уравнений (10.14) для данного счетчика имеем: Е = 9(1001). Отметим, что в соответствии с указанной системой уравнений реализуется управление работой ИМС четырехразрядных двоично-десятичных счетчиков типа КР1533 ИЕ2, КМ155 ИЕ2 и других аналогичных им ИМС.

ИМС рис. 10.8(b) представляет собой четырехразрядный синхронный двоично-десятичный реверсивный счетчик второго типа. В качестве примера такого счетчика можно привести ИМС КР1533 ИЕ12. Предлагаем читателям самостоятельно составить систему уравнений, описывающую алгоритм управления двоично-десятичных реверсивных счетчиков данной разновидности.

10.6. Каскадное построение счётчиков

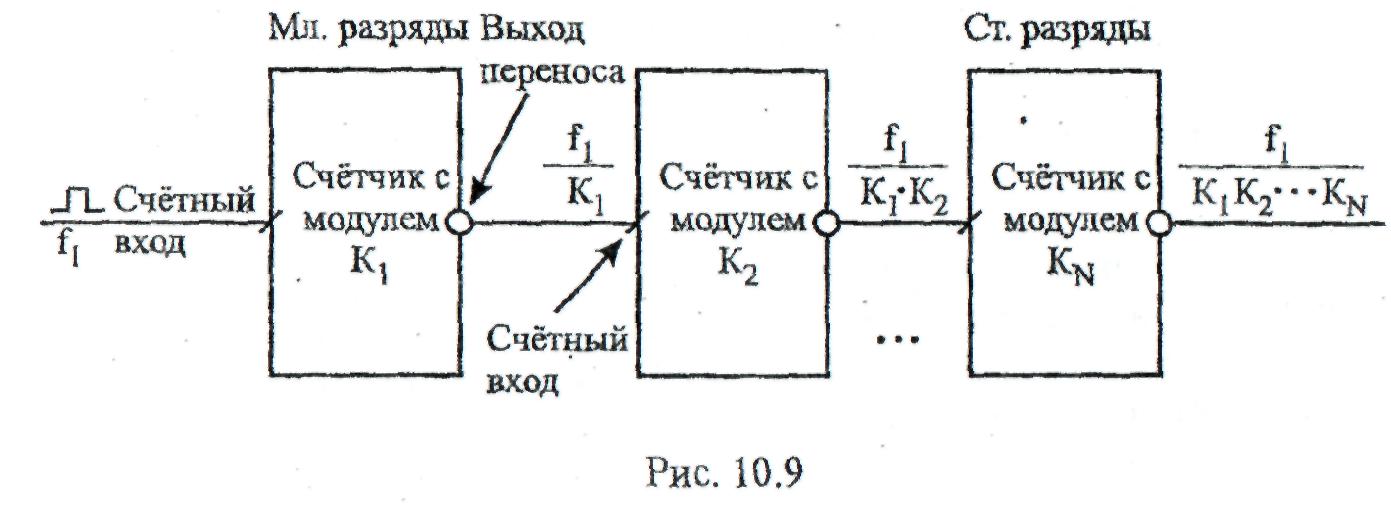
Для построения счётчиков с высоким значением модуля счёта К_к интегральные микросхемы счётчиков с малым значением их мо­дулей K_j могут быть соединены каскадно. В этом случае выходы пе­реноса ИМС счётчиков младших разрядов соединяют со счётными входами ИМС счётчиков старших разрядов (рис. 10.9)

Модуль счёта К_ксчётчика, полученного в результате каскадно­го соединения, равен

Это означает, что на выходе переноса последнего счётчика кас­кадного соединения импульсный сигнал формируется при поступле­нии каждого К_ктактового сигнала. Таким образом, при использова­нии указанного выхода переноса счетчика в качестве информационно­го, счётчик может выполнять функции делителя частоты f_tвходных сигналов в K_kраз. То есть

Аналогично этому на промежуточных выходах переноса счётчи­ка могут быть получены импульсные сигналы с частотой (ƒ₁/K₁·K₂);(ƒ₁/K₁·K₂·K₃) и т.д.

Каскадный счётчик рис. 10.9 работает следующим образом. Пусть в начальный момент все ИМС счётчиков находятся в нулевом состоя­нии, 1=0; N₂=0. N_N =0>. После подачи K₁ импульсов на счёт­ный вход первой ИМС в ней возникает ситуация переполнения и на её выходе переноса формируется сигнал переноса, который поступает на счётный вход второй ИМС и воспринимается ею, как счётный. При этом код числа N₁, зафиксированный в первой ИМС принимает зна­чение 0, а код N₂ числа во второй ИМС увеличивается на единицу. После подачи на вход первой ИМС ещё К₁импульсов ситуация по­вторится.

В том случае, когда соединяемые ИМС счётчиков имеют одина­ковые модули счётаК = К ₂ =. = К _N = К соотношение (10.17) преоб­разуется к виду

Анализ соотношения (10.18) показывает, что каскадный счётчик, построенный на интегральных микросхемах с одинаковым модулем счёта, можно рассматривать как счётчик, выходной, код которого представляет число в позиционной системы счисления по основанию К.

При каскадном построении счётчиков важную роль играет про­цесс формирования сигналов на выходах переноса ИМС, образующих каскадированный счётчик. Рассмотрим особенности каскадного по­строения счётчиков на примере реализации реверсивных счётчиков с высоким значением модуля счёта К_к.

10.6.1. Каскадные счётчики на основе ИМС реверсивных счёт­чиков первого типа.

Интегральные микросхемы реверсивных счетчиков первого типа содержат два выхода переноса:

• инверсный выход прямого переноса 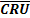и

• инверсный выход обратного переноса .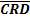

Формирование сигналов на указанных выходах осуществляется в соответствии со следующей системой уравнений:

• • Режим прямого счёта

• •Режим обратного счёта

Соотношения (10.19), (10.20) совместно с полученными ранее со­отношениями (10.12) описывают алгоритм функционирования ИМС реверсивных счётчиков первого типа. Анализ указанных соотношений показывает, что при каскадном соединении ИМС данного типа долж­ны быть выполнены следующее операции:

• В каскадированной цепочке ИМС реверсивных счётчиков вы­ходы прямого переноса 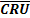каждой предыдущей ИМС должны быть соединены с тактовыми входами счёта на увеличение CUследующих ИМС в

• Для обеспечения возможности установки каскадного счётчика в исходное (нулевое) состояние R— входы всех его ИМС соединяют в параллель. Аналогично этому соединяют входы разрешения парал­лельной загрузки

всех ИМС счётчика для успешной реализации управления режимом предуставки каскадного счётчика в заданное со­стояние.

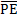
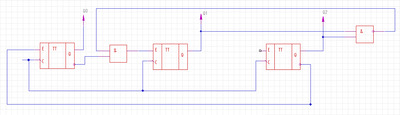
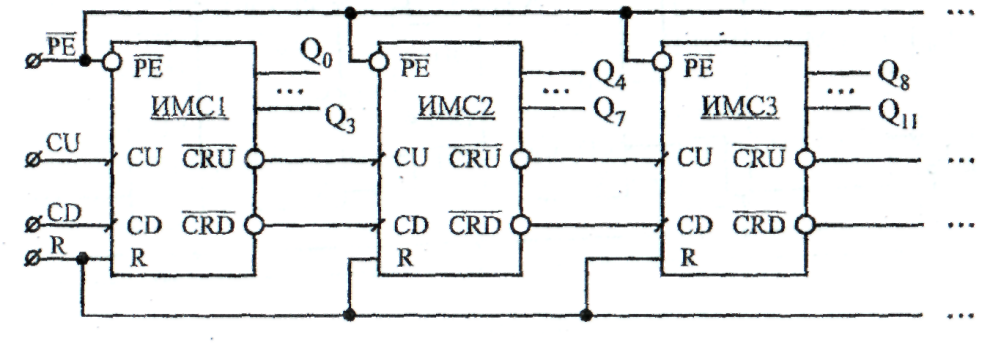
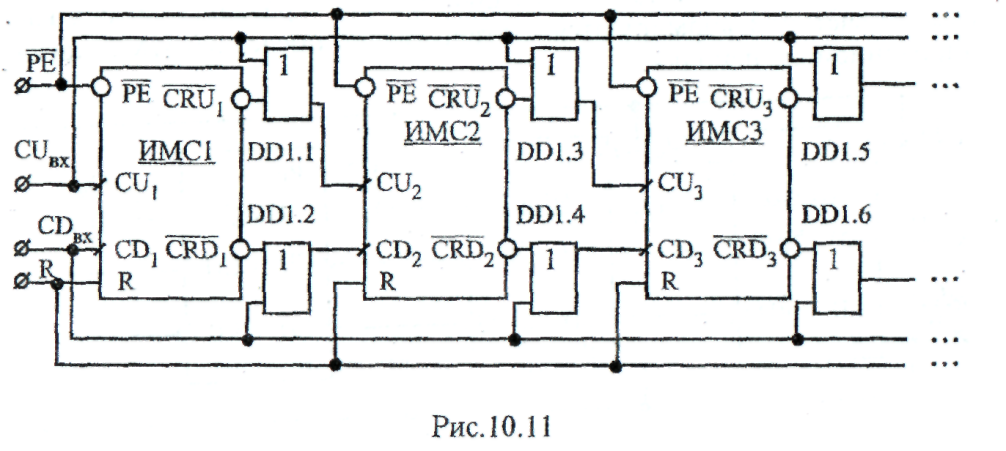
Блок-схема рис. 10.10 иллюстрирует построение реверсивного каскадного счётчика на основе интегральных микросхем реверсивных двоичных счётчиков первого типа. Заметим, что в указанной схеме тактовые входы счёта на увеличение CUи счёта на уменьшение CDпервой в каскадном соединении микросхемы (ИМС1) являются соот­ветственно входами CUи CDкаскадного счётчика в целом, а ин­формационные выходы Q₀,Q₁,Q₂,Q₃ этой ИМС являются выход­ными его младших разрядов.. В свою очередь объединённые в парал­лель R — входы ( 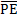— входы) всех ИМС счётчика образуют общий R —вход (РЕ — вход) каскадного счётчика. Старшие разряды числа в кас­кадном счётчике формируются соответственно последней ИМС каска­дированной их цепочки.

где N- число ИМС в каскадном соединении.

Известно, что каскадное построение счётчиков с последователь­ным переносом (рис. 10.9, рис.10.10) характеризуется снижением их бы­стродействия, приводит к возникновению неоднозначности счёта и ложным срабатываниям, присущим в принципе асинхронным счётчи­кам с последовательным переносом. Эти недостатки могут быть уст-

ранены при синхронном построении каскадных счетчиков с реализа­цией в них параллельного переноса.

СU = _j-1+СU_вх (10.22)

СU= _j-1+СD_вх (10.23)

где j <2,3,…,N>.

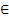
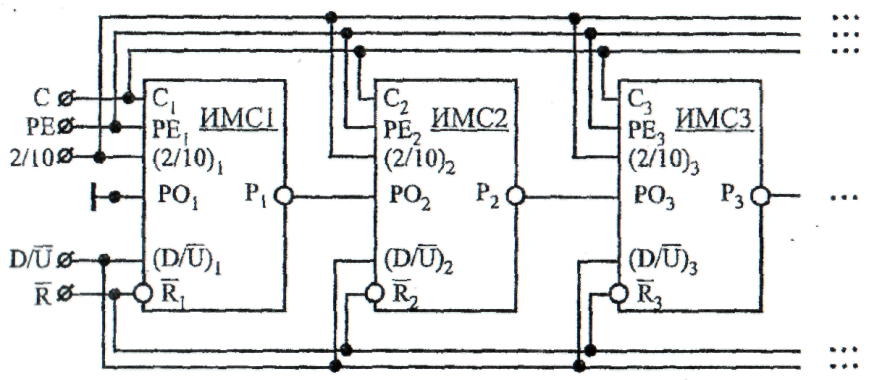
Каскадный счётчик рис. 10.11 работает следующим образом. Ин­тегральная микросхема ИМС₁ выполняет прямой (обратный) счёт входных импульсов CU_BX (CD_BX) от 0 до Е₁(от E₁ до 0), после чего

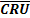
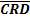
на её выходе ( )формируется «нулевой» сигнал, разрешаю-

Из представленных выше материалов следует, что для синхрон­ного каскадного счётчика с параллельным переносом время задержки распространения сигналов Т_зд может быть определенно из соотноше­ния

Сравнение соотношений (10.24) и (10.21) показывает, что при применении для построения анализируемых схем идентичных ИМС каскадные счётчики с параллельными переносом имеют более высокое быстродействие, чем счётчики с последовательным переносом.

В режиме обратного счёта сигнал переноса (займа) 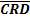форми­руется при переключении счётчика ИМС_j из состояния Nj (t) = 0 в со­стояние N_j (t +1) = E_j. Соответственно при предварительной записи в

счётчик ИМС_j числа N_x сигнал переноса 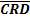появляется в результа­те подсчёта n_j импульсов, поданных на вход CD_j. Где

Предварительная установка счётчика в заданное состояние ши­роко используется в делителях частоты для регулирования их коэффи­циента деления.

10.6.2. Каскадные счётчики на основе ИМС реверсивных счётчиков второго типа

Алгоритм функционирования одиночной интегральной микро­схемы реверсивного счётчика второго типа описывается полученной ранее системой уравнения (10.13). Вместе с тем, для описания функ­ционирования указанной ИМС в каскадном счётчике системы уравне­ний (10.13) оказывается недостаточно. В дополнение к ней должна быть введена система уравнений, описывающая процесс формирова­ния сигналов ИМС на выходе переноса MAXI/MINи на выходе нара­щивания счёта .

Система уравнений, описывающая формирование сигналов пере­носа MAXI/MINв ИМС реверсивных счётчиков второго типа, имеет следующий вид:

— переход из “1” в “0” на выходе MAX/MINпо фронту нарастания сигнала на входеCLK;

1 – “единичное” состояние сигнала, сохраняемого до фронта нарастания сигнала на входе CLK;

0–“нулевое” состояние сигнала, сохраняемого до фронта нарастания сигнала на входе CLK.

Формирование сигналов на выходе наращивания счёта в реверсивных счётчиках второго типа осуществляется в соответствии со следующей системой уравнений:

Типичным примером ИМС реверсивных двоичных счётчиков второго типа является 4- разрядные интегральные ТТЛШ микросхе­мы типа К555ИЕ13, КЕ555ИЕ13-4, КР1533ИЕ13, ЭКФ1533ИЕ13и другие (рис.10.8.в). Соотношения (10.27), (10.28) описывают работу их выходов переноса MAX/MINи наращивания счёта ,что под­тверждается таблицей 10.6 рабочих состояний указанных счётчиков.

Наличие в данных ИМС выхода переноса MAX/MIN,выхода наращивания счёта , а также входа разрешения счёта и тактового входа CLKобеспечивает возможность их каскадного вклю­чения. Действительно, в рассматриваемых интегральных микросхемах имеем:

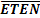
• Счёт реализуется по положительному фронту тактового им­пульса CLKпри «нулевом» уровне напряжения на входе раз­решения счёта

• Напряжение «единичного» уровня на выходе переноса MAX/MINустанавливается при достижении счёта 15(1111)₂для прямого счёта и «ноль» (0000)₂ для обратного

• Установка «нулевого» уровня напряжения на выходе нара­щивания счёта осуществляется при наличии «единич­ного» уровня напряжения на выходе MAX/MIN и низкого уровня напряжения на тактовом входе CLK.Из этого следу­ет, что путём соединения выходов MAX/MINи ИМС предыдущих каскадов со входами и CLK ИМС сле­дующих каскадов может быть построен каскадный ревер­сивный счётчик второго типа, При этом, как и в описанных выше случаях срабатывание ИМС счётчика последующего каскада будет происходить всякий раз по фронту сигнала на его входе CLKпри переполнении ИМС счётчика предыду­щего каскада в режиме прямого счёта, либо при переходе из

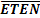
Из рис. 10.12 видно, что для построения каскадного счётчика на основе ИМС рассматриваемого типа необходимо выход переноса P_j-1 каждой ИМС предыдущего каскада соединить со входом переноса PO_j ИМС следующего каскада, а управляющие входы D/ 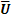, РЕ, С,

счетчик. Их таблицы рабочих режимов представлены в таблицах 10.7 и 10.8 соответственно.

Источник