Что такое результирующая скорость

Что такое результирующая скорость

Формулировка закона:

Как в учебнике Буховцева для 10 класса:

Если тело движется относительно системы отсчета К₁ со скоростью V₁,
а сама система отсчета К₁ движется относительно другой системы отсчета К₂ со скоростью V,
то скорость тела (V₂) относительно второй системы отсчета К₂
равна геометрической сумме векторов V₁ и V.

Упрощаем форммулировку, не меняя смысла:

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.

Вторая формулировка запоминается проще, какой ползоваться решайте сами!

Алгоритм решения задачи на закон сложения скоростей

Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

P.S. В условиях задачи скорости тел заданы обычно относительно неподвижной системы отсчета (например, дороги или берега)

3. Ввести обозначения скоростей (V₁, V₂, V).
4. Сделать чертеж, на котором показать координатную ось ОХ и векторы скорости.
Лучше, если ОХ будет совпадать по направлению с вектором скорости выбранного тела.
5. Записать формулу закона сложения скоростей в векторном виде.
6. Выразить из формулы искомую скорость в векторном виде.
7. Выразить искомую скорость в проекциях.
8. Определить по чертежу знаки проекций.
9. Расчет в проекциях.
10. В ответе не забыть перейти от проекции к модулю.

Пример решения простейшей задачи на закон сложения скоростей

Задача

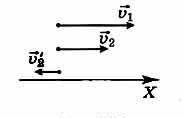
Два автомобиля движутся равномерно по шоссе навстречу друг другу. Модули их скоростей равны 10 м/с и 20 м/с.
Определить скорость первого автомобиля относительно второго.

Решение:

Еще раз! Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

Теперь понятно, что в задаче надо определить V₁.
4. Делаем чертеж, выписываем формулу:

Источник

Закон сложения скоростей

Закон сложения скоростей — что это такое

В классической механике применяют термин, который звучит, как абсолютная скорость точки. Данная величина является суммой двух векторов: относительная и переносная скорости точки. В подобном равенстве выражена теорема сложения скоростей. Общепринятым положением является равенство скорости движения какого-либо объекта в рамках неподвижной системы отсчета и векторной суммы скорости аналогичного физического тела в условиях относительно подвижной системы отсчета. Данными координатами определяется непосредственное нахождение тела.

Классический закон сложения скоростей определяет, что скорость тела относительно неподвижной системы отсчета представляет собой геометрическую сумму двух скоростей, включая скорость тела относительно подвижной системы отсчета и скорость подвижной системы отсчета относительно неподвижной.

Классический вид, формула расчета

Релятивистским законом сложения скоростей являются соотношения, справедливые для частицы, перемещающейся параллельно относительной скорости систем отсчета:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Соотношение теории имеет следующий вид:

В случае, когда u \(u_=u^<,>_+\upsilon\)

Преобразование координат и времени

Спустя какой-то небольшой промежуток времени \(\Delta t^<,>\) частица переместилась в точку:

Таким образом, при движении частицы происходят два события. Можно записать следующую формулу:

где \( \Delta v^<,>_\) представляет собой х компоненту скорости частицы в системе \(K^<,>.\)

Уравнения будут иметь следующий вид:

\(\Delta x=\Delta x^<,>+V\Delta t^<,>\)

Исходя из составленных формул можно сделать вывод о том, что компоненты скорости той же частицы в системе \(К\) будут записаны следующим образом:

Уравнение представляет собой закон сложения скоростей. Данную закономерность можно привести в векторный вид:

Координаты в системе \(К\) и системе \(K^<,>\) будут параллельны.

Алгоритм решения задач

Существуют правила, которые являются основой механической физики. Исходя из данных соотношений, можно рассмотреть примеры сложения скоростей. Простейшими объектами для объяснения физических законов являются, к примеру, человек и любой перемещающийся в пространстве объект, с которым он прямо или косвенно взаимодействует.

Пример

Можно представить, что человек совершает прямолинейное движение вдоль коридора пассажирского поезда со скоростью пять километров в час. При этом равномерная скорость состава составляет 100 километров в час. Скорость человека, относительно пространства, которое его окружает, будет равна 105 километрам в час. Следует учитывать одинаковое направление перемещения человека и поезда.

В случае, когда направления движения человека и транспорта противоположны, данный принцип также справедлив. Тогда человек будет двигаться относительно окружающего пространства со скоростью 95 километров в час.

При рассмотрении объектов, скорости которых равны, можно сделать вывод, что относительно друг друга они неподвижны. Во время вращения скорость рассматриваемого тела представляет собой совокупность скоростей перемещения тела относительно движущейся поверхности другого объекта.

Решение задач на сложение скоростей выполняется в несколько этапов:

Задача 1

На примере рассмотрено равномерное движение двух поездов друг за другом. Первый поезд перемещается со скоростью 80 км/ч, а второй — 60 км/ч. Требуется рассчитать, какова скорость второго поезда относительно первого.

Решение

Следует обозначить скорость первого транспортного средства по отношению к земле с помощью \(\vec>.\)

Тогда скорость второго поезда составит \(\vec>.\)

Исходя из закона сложения скоростей:

где \(\vec^<'>>\) является искомой скоростью второго поезда по отношению к первому.

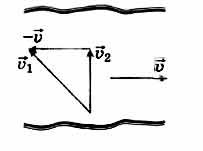
Такой метод сложения скоростей наглядно представлен на рисунке. Схематично скорость второго поезда по отношению к первому направлена противоположно направлению перемещения поездов, и можно наблюдать удаление второго поезда от первого. Проекция скорости \(\vec^<'>>\) на ось ОХ будет записана таким образом:

Задача 2

Река течет со скоростью \(v = 1,5\) м/с. Требуется определить модуль скорости \(v_<1>\) по отношению к воде. Необходимо учитывать, что в случае движения катера перпендикулярно относительно берега, его скорость составляет \(v_<2>=2\) м/с.

Решение

Исходя из закона сложения скоростей:

Формула для расчета скорости катера относительно реки:

Векторное сложение скоростей представлено на рисунке. На схеме получаем треугольник скоростей с прямым углом, поэтому:

Ответ: модуль скорости \(v_<1>\) по отношению к воде составляет \(2,5\) м/с.

Задача 3

Скорость движения самолета относительно воздуха составляет 300 км/ч. Объект движется в северном направлении. При возникновении северо-западного ветра, скорость которого 100 км/ч по отношению к земле, самолет должен сохранить исходное направление. Требуется рассчитать угол, под которым летчик удерживает направление самолета для продолжения пути на север, а также скорость самолета относительно земли.

Решение

Необходимо связать неподвижную систему отсчета с землей, а подвижную — с воздухом. Скорость самолета по отношению к земле можно рассчитать, как сумму скорости самолета относительно воздуха и скорость ветра относительно земли. В таком случае, исходя из закона сложения скоростей:

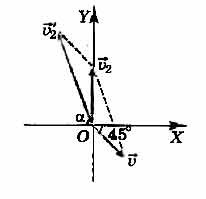
Рисунок демонстрирует направление этих скоростей. Направление скоростей выполнено таким образом, чтобы проекции скорости самолёта относительно ветра и скорости ветра на оси ОХ равнялись по модулю и были направлены противоположно:

Если рассматривать проекцию на ось ОУ, то уравнение примет такой вид:

В таком случае, искомая скорость самолета составит:

Данное равенство позволит определить угол α:

Подставив числовые характеристики, получим:

Найти \(\sin \alpha\) можно таким образом:

Скорость самолета относительно земли составит:

Ответ: угол, под которым летчик удерживает направление самолета для продолжения пути на север, равен \(76^<0>\) ; скорость самолета относительно земли примерно равна 220 км/ч.

Источник

Сложение скоростей

Всего получено оценок: 110.

Всего получено оценок: 110.

Скорость — это одна из кинематических характеристик движения. При описании движения в различных системах отсчета возникает вопрос о сложении скоростей. Рассмотрим общие принципы этой операции.

Применение операции сложения

Когда говорят о сложении, как правило, подразумевают ситуацию, в которой есть две величины и необходимо найти третью, которая является объединением двух первых.

Арифметическую операцию сложения изучают в младшей школе, в задачах вроде: «У Ани два яблока, а у Бори одно, сколько всего яблок у детей?». Арифметически складывая обе исходных величины, в итоге получаем ответ «три».

Рис. 1. Сложение в первом классе.

Однако арифметическое сложение годится далеко не во всех случаях.

В самом деле, если два ученика одновременно выходят из дома и через 15 минут одновременно приходят в класс, то на вопрос «сколько ученики вместе провели в пути» пользоваться арифметическим сложением нельзя, поскольку при сложении мы получим 30 минут, а реально ученики провели в пути только 15 минут.

Есть и более интересные примеры, когда арифметическое сложение при объединении не подходит.

Представьте две реки с одинаковым руслом, катящие мелкие камни. Самые большие камни, катящиеся в первой реке, весят 1 г. А вторая река может катить камни размером на 25 % больше (они весят по 2 г). Если обе этих реки пустить по одному такому руслу, камни какого размера сможет катить такая река? В 2,25 раз больше чем в первой реке? Не угадали. Арифметическое сложение здесь не работает. Река сможет катить камни в 4,5 раза больше, чем в первой реке. Их вес будет равен 90 г!

Сложение скоростей

Сложение скоростей в механике — это один из случаев, когда арифметическая операция сложения не подходит для определения результата.

Причина этого состоит в том, что скорость — векторная величина. Она имеет не только величину, но и направление. И это направление непосредственно влияет на результат сложения.

Действительно, представим себе эскалатор, движущийся вверх со скоростью 1 м/с. Если двигаться по нему вверх с той же скоростью, то с точки зрения наблюдателя рядом с эскалатором, человек будет двигаться вверх со скоростью 2 м/с. Однако, если человек будет двигаться вниз, то его скорость для наблюдателя будет равна нулю.

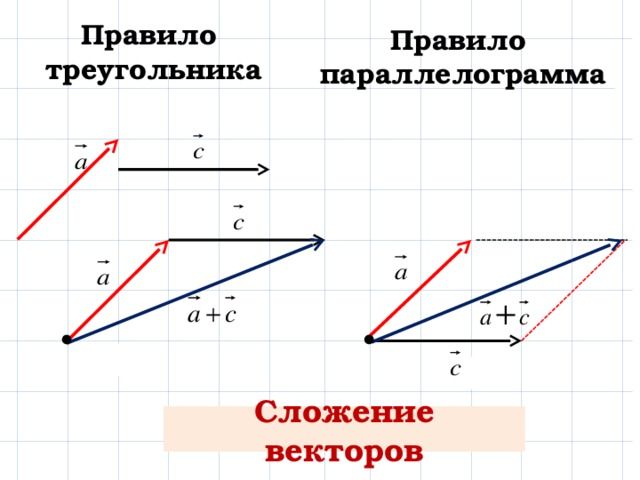
Движение по эскалатору — это пример сложения скоростей, направленных вдоль одной прямой, когда достаточно одной координатной оси. Если движение происходит на плоскости, где требуются две координатных оси, или в пространстве с тремя координатами, то для сложения скоростей необходимо пользоваться правилами сложения векторов. Формула сложения скоростей принимает вид:

$$\overrightarrow v_<общ>=\overrightarrow v_1+\overrightarrow v_2+…+\overrightarrow v_n$$

В общем случае необходимо проецировать векторы на оси координат, складывать или вычитать их величины в зависимости от направления и потом по получившимся координатам строить векторный результат.

Рис. 3. Сложение векторов.

Что мы узнали?

Скорость — векторная величина, имеющая не только величину, но и направление. Поэтому арифметическая операция сложения не годится для сложения скоростей. В данном случае необходимо использовать правила сложения векторов.

Источник

Относительное движение

Скорость. Сложение скоростей.

Скорость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчета.

Единицы измерения: \(\displaystyle [\text<м>/\text<с>]\) (метр в секунду).

Правило (закон) сложения скоростей

Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.

Рассмотрим вывод закона сложения скоростей.

Предположим теперь, что муха поползла по вагону. Тогда появляются ещё две скорости, которые нужно рассмотреть. Скорость мухи относительно вагона (то есть в движущейся системе \(\displaystyle K’\) ) обозначается \(\displaystyle \vec\) и называется относительной скоростью.

Скорость мухи относительно земли (то есть в неподвижной системе \(\displaystyle K\) ) обозначается \(\displaystyle \vec\) и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.

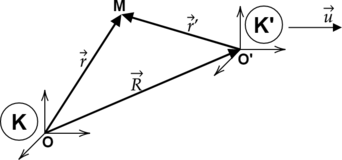
На вышеприведенном рисунке муха обозначена точкой M. Далее,

\(\displaystyle \vec\) — радиус-вектор точки M в неподвижной системе \(\displaystyle K\) ;

\(\displaystyle \vec\) — радиус-вектор точки M в движущейся системе \(\displaystyle K’\) ;

Источник

Большая Энциклопедия Нефти и Газа

Результирующая скорость

Результирующая скорость будет направлена по диагонали куба из точки О. [1]

Результирующая скорость этих процессов определяется разностью скоростей прямого и обратного процессов. [2]

Результирующая скорость в любой точке контура единичного круга для течения с подъемной силой получается алгебраическим сложением скоростей, вызванных отдельными потоками, так как круговой контур является линией тока для каждой из трех частей потока. [3]

Результирующая скорость будет направлена по диагонали куба из точки О. [6]

Результирующая скорость потока в элементарном объеме в направлении х находится перемножением приведенных выше выражений. [8]

Результирующие скорости диффузии и миграции обусловлены большим количеством перескоков ионов за единицу времени в некотором определенном направлении по сравнению с другими направлениями. [9]

Результирующая скорость строгания является переменной величиной, изменяющейся от нуля в крайних положениях резца до максимума в середине, и траектория резца по длине хода L криволинейна. [11]

Результирующая скорость травления при стационарном процессе определяется единичными скоростями диффузии и химической реакции на поверхности кристалла. [12]

Результирующая скорость полимеризации пропорциональна корню квадратному из концентрации перекиси, однако сама скорость распада очень зависит от растворителя и концентрации мономера. [13]

Результирующая скорость потока в элементарном объеме в направлении х находится перемножением приведенных выше выражений. [15]

Источник