Что такое робастная система
Робастные системы управления
Исследование устойчивости систем управления при наличии неопределенности в пространстве параметров (робастная теория). Задача синтеза робастных систем управления. Объекты управления с мультипликативной погрешностью (неопределенностью), их схема.
| Рубрика | Коммуникации, связь, цифровые приборы и радиоэлектроника |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 19.03.2016 |
| Размер файла | 366,9 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru
Размещено на http://www.allbest.ru
Робастные системы управления
1. Актуальность темы
2. Робастное управление
3. Параметрические неопределенности
4. Непараметрические неопределенности
5. Критерии устойчивости для цифровых систем
При моделировании систем управления учет неопределенности всегда являлся одной из основных задач. Одна из первых моделей неопределенности (нелинейная) была предложена в работах А.П. Лурье (1951), М.А. Айзермана (1961), Ф.Р. Гантмахера (1967). Модели параметрической неопределенности в линейных системах появились позднее. Их систематическое изучение начал И. Горовиц (1970). Важное направление в анализе неопределенности связано с моделью неизвестных, но ограниченных возмущений. Большой вклад в это направление внесли А.Б. Куржанский и Ф. Л. Черноусько. Модели частотной неопределенности интенсивно разрабатывались в 1980 гг., вероятностный подход к робастности получил большое развитие в последнее десятилетие.
Основными задачами робастной устойчивости, с одной стороны, являлось определение границ устойчивости в пространстве параметров системы первого приближения (И.А. Вышнеградский), а с другой, получение оценок области асимптотической устойчивости расчетных режимов исходных систем.
Исследование устойчивости систем управления при наличии неопределенности в пространстве параметров (робастная теория) является весьма важным и актуальным направлением научных исследований, т.к. позволяет, на этапе проектирования, определить, является ли устойчивым весь класс рассматриваемых систем. Это позволяет обеспечить безопасное функционирование управляемого объекта, несмотря на то, что в процессе изготовления и эксплуатации его параметры хотя и могут отличаться от расчетных, но гарантировано будут отвечать устойчивому поведению этого объекта, т.к. они принадлежат области робастной устойчивости. Заметим, что разработка методов решения задач робастной устойчивости, является весьма сложной проблемой. Например: устойчивость всех вершинных и реберных матриц семейства не обеспечивает робастной устойчивости всего этого семейства и, поэтому на практике, усилия инженеров и конструкторов направлены на решение конкретных задач.
Методы расчета робастной устойчивости систем управления (робастное управление) включают в себя как известные подходы, например, теорию возмущений, так и новые: м-анализ (J.C. Doyle, A. Packard, Б.Т. Поляк) и вероятностный подход к робастности (R.F. Stengel, L.R. Ray и др.).
Разработке и созданию методов исследования различных задач робастной устойчивости посвящено множество работ, принадлежащих как отечественным, так и зарубежным ученым, таким как И.А. Вышнеградский, Я.З. Цыпкин, Б.Т. Поляк, В.Л. Харитонов, П.С. Щербаков, А.С. Немировский, Ю.П.Петров, М.Г. Сафонов, B.R. Barmish, J. Ackermann, V. Blondel, J. Kogan, R. Tempo, D.D. Siljak и др.
Актуальность исследований робастной устойчивости в системах управления диктуется, во-первых, современными потребностями науки и техники и ее приложениями в практических задачах, связанных с конструированием и моделированием процессов управления в технике, экономике, биологии и т.д.; во-вторых, наличием большого числа нерешенных задач, прямо связанных с инженерной практикой. Фактически результаты, полученные в теории робастной устойчивости, позволяют обеспечивать динамическую безопасность управляемых систем на этапе их конструирования и эксплуатации.
Задача синтеза робастных систем управления заключается в поиске закона управления, который сохранял бы выходные переменные системы и сигналы ошибки в заданных допустимых пределах, несмотря на наличие неопределённостей в объекте управления.[4,5] Обычно робастные контроллеры применяются для управления объектами с неизвестной или неполной математической моделью, и содержащими неопределённости (рис.1)
3. Параметрические неопределенности
Рассмотрим систему, в которой:
— характеристический полином замкнутой системы
Замкнутая система будет устойчива при:
Следовательно условие робастной устойчивости примет вид:
4. Непараметрические неопределенности
Непараметрическая неопределенность задает допустимую ошибку в частотной области.
Аддитивная неопределенность и мультипликативная неопределенность
Каждый объект управления F(s) как элемент множества объектов сверху ограничен ошибкой в аддитивной форме и может быть формально представлен следующей структурной схемой (рис.2)
Рисунок 2-Номинальный F(jw) объект управления с аддитивной ошибкой
Структурная схема объектов с мультипликативной неопределенностью показана на рис.3
робастный управление мультипликативный погрешность
Аддитивные и мультипликативные неопределенноости модели объекта управления не могут использоваться для представления множества объекта у которых в последствии изменения параметров или в следствии структурной неопределенности появляються дополнительные полюса справа от комплексной оси, т.е. объектов у которых количество «правых» полюсов может меняться.[8,9,10]
Теорема о малом коэффициенте усиления:
система с регулятором C(s) и номинальным объектом P0(s) робастно устойчива, если для любой частоты щ выполняется неравенство:
Критерии устойчивости для цифровых систем
Все критерии устойчивости, которые используются для анализа устойчивости непрерывных систем, могут быть использованы для дискретных систем с учетом некоторых особенностей.
Критерий устойчивости Гурвица можно использовать при применении билинейного преобразования. Рассмотри алгоритм его использования.
1. Записываем характеристическое уравнение D(z) = 0
3. Составляем определитель Гурвица
4. Определяем устойчивость также как и для непрерывных систем.
Линейная дискретная система устойчива, если при a0>0 определитель Гурвица и все его диагональные миноры положительны.
Рассмотрим частные случаи.
При n = 1 характеристическое уравнение имеет вид
При n = 2 характеристическое уравнение имеет вид
Условие устойчивости: a0 > 0, a1 > 0, a2 > 0, а также:
Критерий устойчивости Михайлова с использованием билинейного преобразования
При этом исходным является характеристический полином в форме z-преобразования. Выполним подстановку
При этом критерий Михайлова для дискретных систем применяется в таком же виде, как и для непрерывных систем.
Критерий устойчивости Найквиста
Рассмотрим функцию, которая связывает характеристики разомкнутых и замкнутых дискретных систем
В соответствии со следствием из принципа аргумента
Рассмотрим разные случаи.
Система, устойчивая в разомкнутом состоянии
Так как разомкнутая дискретная система устойчива, то она не содержит корней в правой полуплоскости (т. е. m = 0), для того чтобы и замкнутая дискретная система была устойчива, должно выполняться условие
Формулировка критерия Найквиста:
Графически это обозначает, что годограф вектора W*(j?) не охватывает начала координат, а вектора K*(j)-точку с координатами (-1, j0).
Система, неустойчивая в разомкнутом состоянии
Так как разомкнутая система неустойчива, то она содержит m корней в правой полуплоскости, для того чтобы замкнутая система была устойчива, должно выполняться условие:
На данный момент было проведено исследование существующих методов оценки робастной устойчивости и робастного качества. Полученные в ходе исследования результаты, будут учитываться при дальнейшем обучении
7. Н.Т. Кузовков. Модальное управление и наблюдающие устройства. М. : Машиностроение 1967- 342с.
Размещено на Allbest.ru
Подобные документы
Общие принципы построения систем автоматического управления, основные показатели их качества. Передаточная функция разомкнутой и замкнутой систем. Определение устойчивости системы. Оценка точности отработки заданных входных и возмущающих воздействий.
реферат [906,1 K], добавлен 10.01.2016
Выполнение синтеза и анализа следящей системы автоматического управления с помощью ЛАЧХ и ЛФЧХ. Определение типов звеньев передаточных функций системы и устойчивости граничных параметров. Расчет статистических и логарифмических характеристик системы.
курсовая работа [1,9 M], добавлен 01.12.2010
Исследование устойчивости линейной САУ различными методами анализа (частотными и алгебраическими) с применением двух программных пакетов Mathcad и Matlab-Simulink. Общая передаточная функция с числовыми значениями. Структурная схема системы управления.
курсовая работа [1,5 M], добавлен 01.06.2015
Определение устойчивости и оценки качества систем управления. Расчет устойчивости Гурвица. Моделирование переходных процессов. Задание варьируемого параметра как глобального. Формирование локальных критериев оптимизации. Исследование устойчивости СУ.
курсовая работа [901,9 K], добавлен 19.03.2012
Математическая модель объекта управления в пространстве состояния. Структурная схема и сигнальный граф. Формула Мейсона и передаточная функция объекта управления. Матричное уравнение для выходной переменной. Условия устойчивости системы и ее корни.
курсовая работа [514,1 K], добавлен 12.05.2009
Решение задачи синтеза корректирующего устройства при коррекции систем управления. Передаточная функция интегрирующей цепи. Методы синтеза последовательных корректирующих устройств и их классификация. Их логарифмические частотные характеристики.
контрольная работа [66,9 K], добавлен 13.08.2009
Функциональная схема замкнутой системы. Анализ устойчивости исходной линеаризованной системы по алгебраическому критерию. Построение среднечастотного и высокочастотного участков. Анализ качества системы в переходном режиме. Отработка входных сигналов.
дипломная работа [640,5 K], добавлен 15.02.2016
Робастное управление
Робастность [англ. robust [1]
Для проектирования робастных систем управления используются различные методы оптимального и робастного синтеза, среди которых синтез контроллеров в пространствах H∞ и H2, ЛМН-контроллеры, μ-контроллеры.
Содержание
Задача робастного управления [ | ]
Главной задачей синтеза робастных систем управления является поиск закона управления, который сохранял бы выходные переменные системы и сигналы ошибки в заданных допустимых пределах несмотря на наличие неопределённостей в контуре управления. Неопределённости могут принимать любые формы, однако наиболее существенными являются шумы, нелинейности и неточности в знании передаточной функции объекта управления.
Общая каноническая задача робастного управления математически описывается в следующем виде:
1 K M ( T y 1 u 1 ( j ω ) ) 1 <\displaystyle <\frac <1>
Для того, чтобы внести в робастный синтез требования по качеству управления, используется фиктивная неопределённость Δ n <\displaystyle \Delta _
В робастном анализе требуется найти K M <\displaystyle K_
Структурные и неструктурные неопределённости [ | ]
В робастном управлении рассматриваются два вида неопределённостей — структурные и неструктурные. Неструктурные неопределённости обычно представляют собой элементы, зависящие от частоты, такие как, например, насыщение в силовых приводах или возмущения в низкочастотной области АФЧХ объекта управления. Воздействие неструктурных неопределённостей на номинальный объект управления может быть как аддитивным
так и мультипликативным
G = ( I + Δ M ) G n o m <\displaystyle G=(I+\Delta _
Структурные неопределённости представляют собой изменения в динамике объекта управления, к примеру:
Общий подход, сформулированный в канонической задаче робастного управления, позволяет выявить на этапе проектирования как структурные, так и неструктурные неопределённости и использовать их в процессе синтеза робастного контроллера.
Робастный анализ [ | ]
Робастный синтез [ | ]
Целью робастного синтеза является проектирование такого контроллера, который бы удовлетворял критерию робастности. Начиная с 50-х годов XX века был разработан ряд процедур и алгоритмов, позволяющих решить задачу робастного синтеза. Робастные системы управления могут сочетать черты как классического управления, так и адаптивного и нечёткого.
Ниже представлены основные технологии синтеза робастных систем управления:
Робастное оценивание
Материал из MachineLearning.
Содержание
Введение
Мы будем понимать под термином робастность нечувствительность к малым отклонениям от предположений. Процедура робастна, если малые отклонения от предположенной модели должны ухудшать качество процедуры (например, асимптотика дисперсии или уровень значимости и мощность критерия) должны быть близки к номинальным величинам, вычисленным для принятой модели.
Рассмотрим робастность по распределению, т.е. ситуации, в которых истинная функция распределения незначительно отличается от предполагаемой в модели (как правило, гауссовской функции распределения). Это не только наиболее важный случай, но и наиболее полно изученный. Гораздо меньше известно о том, что происходит в тех ситуациях, когда несколько нарушаются прочие стандартные допущения статистики, и том, какие меры защиты должны предусматриваться в подобных случаях.
Основные типы оценок
Введем оценки трех основных типов ( ),буквы отвечают соответственно оценкам типа максимального правдоподобия, линейным комбинациям порядковых статистик и оценкам, получаемых в ранговых критериях.
Оценки типа максимального правдоподобия (M-оценки)
или как решение неявного уравнения
В частности, нас будут интересовать оценки сдвига
Последнее уравнение можно записать в эквивалентном виде
Тогда мы можем представить оценку в форме взвешенного среднего
Линейные комбинации порядковых статистик (L-оценки)
Рассмотрим статистику, которая представляет собой линейную комбинацию порядковых статистик или, в более общей постановке, значений на некоторой функции :
Предположим, что весовые коэффициенты порождаются при помощи (знакопеременной) меры на интервале (0,1):
В рассматриваевом случае оценка получается при помощи функционала
Далеко не все порядковые статистики являются робастными. Максимум, минимум, среднее и полусумма максимума и минимума не являются робастными, их характеристика, показывающая сколько наблюдения можно изменить, чтобы это не повлияло на конечный результат, равна 0. У робастных оценок эта характеристика равна 50% в случае медианы, а в остальных меньше и зависит от процента, используемого для отсечения данных.
Оценки, получаемые в ранговых критериях (R-оценки)
Как правило, мы полагаем, что весовые коэффициенты получаются при помощи некоторой функции по формуле
В действительности предпочитают работать со следующим вариантов вычисления
который при подстановке примет вид
На практике работают с последним. Кроме того, работаем с условием того, что
В этих предположениях математическое ожидание статистики при нулевой гипотезе равно 0.
Оценки сдвига в двухвыборочной постановке и сдвига в случае одной выборки можно получить при помощи следующих ранговых критериев.
Вычисление робастных оценок
Робастность, связанная с регрессией, носит особый характер, и здесь возникают довольно сложные задачи. В случае линейной регрессии используется метод наименьших квадратов. Здесь мы работаем с М-оценками.
Тогда решение сводится к следующему:
Затем по псевдонаблюдениям вычисляются новые значения подгонки (и новые ). Действия повторяются до достижения сходимости.
Очевидно, что эта процедура сводит на нет влияние выделяющихся наблюдений.
Что такое робастная система
При проектировании систем управления многими динамическими объектами в условиях параметрической неопределенности, как правило, известны только оценки параметров объекта управления в виде верхних и нижних граничных значений, либо задана принадлежность параметров некоторому множеству. К таким объектам относятся биотехнологические объекты стадии ферментации фармацевтических и микробиологических производств [4]. Поэтому проектируемые регуляторы должны обеспечивать устойчивость и качество не одной системы управления, а целого семейства систем, соответствующих различным значениям параметров объекта. Это достигается путем придания системам свойств робастной устойчивости и робастного качества по отношению к параметрическим и иным возмущающим воздействиям за счет выбора структуры системы и синтеза соответствующих алгоритмов управления [1, 8].
Одним из методов синтеза таких алгоритмов управления является использование аппарата нечёткой логики [2, 7]. Однако общих рекомендаций по синтезу и анализу робастных систем для управления биотехнологическими объектами нет. В связи с этим актуальными являются вопросы анализа и синтеза робастной системы управления с нечетким регулятором на основе принципа переменной структуры, функционирующей в условиях параметрической неопределенности, нестационарности и при наличии запаздывания управляемых биотехнологических объектов. Под переменной структурой в данной работе понимается изменение связей между функциональными блоками нечеткой системы в зависимости от характера колебаний регулируемой переменной в переходном процессе системы.
Синтез нечеткого регулятора с переменной структурой
Повышение требований к качеству регулирования и увеличение числа факторов, оказывающих значимое влияние на функционирование объектов управления, ведут в общем случае к усложнению синтезируемых регуляторов. Практика же требует создания регуляторов как можно более простой структуры. К таким регуляторам из типовых можно отнести релейные, двух-, трехпозиционные регуляторы. Однако известно [4], что используемые к настоящему времени позиционные регуляторы не всегда обеспечивают заданное качество регулирования. В связи с этим для улучшения качества позиционного регулирования разработаны модифицированные варианты алгоритмов управления, полученные на основе аппроксимации характеристик нелинейных типовых элементов и различных их комбинаций непрерывными нелинейными функциями типа сигмоидных [4]. К последним относится регулятор, синтезированный на основе аппроксимации характеристик релейного элемента с зоной и без зоны нечувствительности с насыщением, названный аппроксимированным нелинейным функциональным регулятором – АНФ-регулятором [4]. Закон управления, реализуемый этим регулятором, имеет следующий вид:
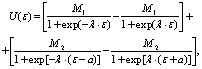
где М1, М2 – величина регулирующего воздействия в зоне нечувствительности (ЗН) и за ее пределами соответственно; ε – ошибка регулирования; λ – коэффициент, определяющий наклон линейного участка характеристики регулятора; 2а – величина ЗН.
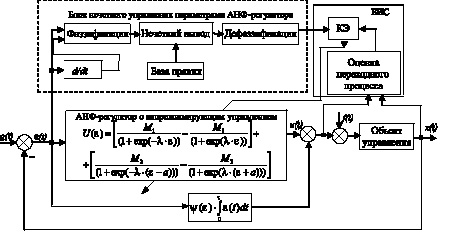
Структурно разрабатываемая интеллектуальная САУ содержит дополнительные блоки, которые выполняются как надстройка над АНФ-регулятором прямой цепи САУ, настраивая нужным образом его параметры (рис. 1). Основная функция, возлагаемая в данном случае на нечеткий регулятор (НР), – это формирование корректирующих поправок к коэффициентам настройки М1, М2 АНФ-регулятора в зависимости от текущего значения и скорости изменения ошибки регулирования. Функциональная схема нечеткой системы управления с использованием динамически корректируемого АНФ-регулятора приведена на рис. 1.
Рис. 1. Структурная схема нечеткой САУ с АНФ-регулятором в прямой цепи: КЭ – ключевой элемент; БИС – блок изменения структуры
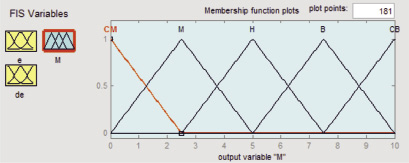
Входными сигналами нечеткого регулятора выбраны сигнал рассогласования и его производная. Выходом – величина корректирующего воздействия на параметры М1, М2 АНФ-регулятора в прямой цепи системы. Для этого в лингвистических переменных нечеткой логики коррекция параметра М1, М2 представлена следующими пятью термами: сильно уменьшить (СМ), уменьшить (М), норма (Н), увеличить (В) и сильно увеличить (СВ).
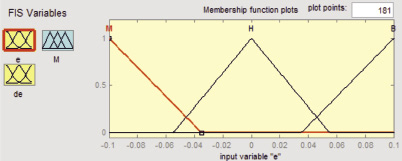
Форма функций принадлежности для простоты математического описания выбрана треугольной. Числовые значения функций принадлежности выбраны исходя из возможных диапазонов изменения входных и выходной переменных, полученных при экспериментальном исследовании алгоритма аппроксимирующего управления [3, 4]. Известно, что степень пересечения во входных функциях принадлежности сильно влияет на статические характеристики нечеткого регулятора [5]. В то время как маленькие пересечения во входных функциях принадлежности формируют пороговые (ступенчатые) характеристики, большие пересечения делают кривую более гладкой. Пересечения в выходных функциях принадлежности меньше влияют на характеристику. Как видно из рис. 2, а, функции принадлежности для ошибки регулирования выбраны с небольшим пересечением оснований, так как гладкость кривой обеспечена параметрами аппроксимирующей функции.
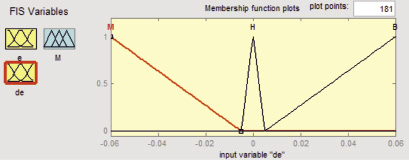
Рис. 2. Графики функций принадлежности (а – ошибка, б – скорость изменения ошибки, в – корректируемый параметр регулятора)
Функция принадлежности входного сигнала ε(t) имеет два пересечения (перекрытия) на интервалах [– 0,055; – 0,035] и [0,055; 0,035], которые точно соответствуют диапазонам положительных наклонов кривой. Причиной тому является то, что два правила в этих диапазонах одновременно активны. С другой стороны, на диапазонах без пересечения только одно правило активно. Функция принадлежности выходного сигнала в этом случае зависит только от степени активности и, таким образом, центр тяжести функции принадлежности остается неизменным.
При синтезе системы использован алгоритм логического вывода по Мамдани как наиболее простой и позволяющий выносить суждение о том или ином параметре в виде утверждений, в отличие от их представления линейными функциями, характерного для нечеткого вывода Сугено. Значения функций принадлежности соответствующих нечётких переменных представлены в виде кусочно-линейных графиков, показанных на рис. 2.
Для дефаззификации переменных, т.е. для перехода от нечетких выводов к точному значению корректируемого параметра М, использован метод центра тяжести [9].
Следует заметить, что поскольку объект управления и АНФ-регулятор являются статическими звеньями, то при конечных значениях λ, М1, М2 в замкнутой САУ возникает статическая ошибка. Для сведения ее к нулю и придания системе свойства астатизма в алгоритм управления нечеткой системы с АНФ-регулятором введен интегратор с коэффициентом интегрирования ψ(ε). На основе вышеприведенных соображений и предложенного принципа управления в программном пакете Мatlab была реализована система с нечетким регулятором (рис. 1).
Результаты исследования нечёткой системы управления
В качестве объекта управления рассмотрен биореактор-ферментатор периодического действия по каналу регулирования температуры. При исследовании свойств системы удобно воспользоваться описанием объекта управления в виде передаточных функций [5]. Считаем априори известными значения параметров интервальной модели объекта, представленной в форме передаточной функции следующего вида:
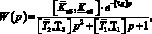
в которой класс неопределенности задан неравенствами для коэффициента передачи объекта 
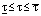
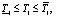
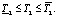

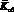
Интервально-заданный объект управления с запаздыванием по каналу регулирования температуры в ферментаторе, аппроксимированный моделью c передаточной функцией вида
W(p) = Коб•ехр(– τ•p)/(T22•p2 + T1•p + 1), (3)
где 0,087 ≤ Коб ≤ 0,383; 14,35 ≤ T1 ≤ 41,56; 8,55 ≤ T2 ≤ 25,0; 2,2 ≤ τ ≤ 6,0, можно представить как семейство квазистационарных объектов.
Учитываем [6], что при описании объекта с параметрической неопределенностью номинальная модель располагается в центре множества. С учетом этого параметры номинальной модели объекта были заданы в виде среднеинтервальных значений:

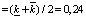
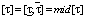
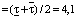
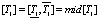
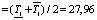
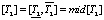
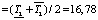
где 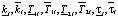
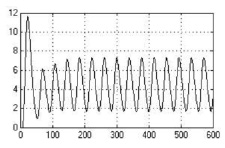
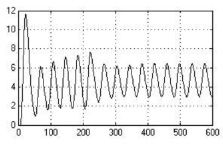
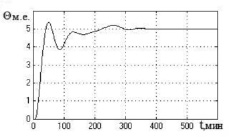
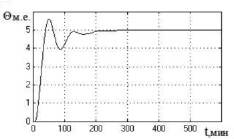
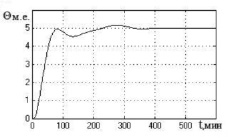
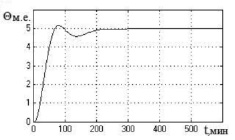
Исследование нечёткой системы управления проведено путем имитационного моделирования при подаче на вход системы задающего воздействия θзад = 5 м.е. и подаче на вход объекта в различные моменты времени единичного ступенчатого воздействия f = 10 м.е. (м.е. – машинные единицы). В качестве значений параметров настройки АНФ-регулятора в основном контуре системы использованы следующие: М1 = М, М2 = М/2; λ = 0,2456; a = 0,1; M1 = 7, M2 = 14. Для анализа робастного качества проведены исследования САУ с моделью при неблагоприятном сочетании интервальных параметров объекта, которое характеризует предельно возможное качество робастного управления [1]. Полученные переходные процессы представлены на рис. 3.
Рис. 3. Переходные процессы в нечеткой САУ при выводе объекта на заданный режим (а) и действии возмущения на входе объекта в момент времени t = 200 мин (б) с моделью с неблагоприятным сочетанием параметров объекта: по оси ординат – регулируемая переменная, по оси абсцисс – время в мин
Из рис. 3 видно, что настройка нечеткого АНФ-регулятора, выполненная с использованием номинальной модели объекта, не исключает автоколебания при выводе на режим объекта при наихудшем сочетании параметров и поэтому не является оптимальной. Известно, что значительный ряд технологических процессов, особенно процессов биосинтеза, реакторных, химических и др., не допускает автоколебательного режима. Следовательно, существует необходимость в автоматической подстройке параметров регулятора или коррекции структуры системы. Однако подстройка параметров λ и М алгоритма управления (1) не приводит к положительному результату. Так, с уменьшением М уменьшается колебательность, но затягивается переходный процесс и имеет место статическая ошибка (при отсутствии интегрирующего звена). В связи с этим в данной статье рассмотрено решение задачи с помощью изменения структуры системы.
Для изменения структуры САУ (рис. 1) в состав нечеткого регулятора введена дополнительная корректирующая логическая связь по динамике переходного процесса. Возможны различные оценки динамики переходного процесса. Например, если ошибка большая (положительная или отрицательная) и скорость ее изменения большая, но другого знака, то сигнал управляющего воздействия НР должно быть минимальным, так как ошибка быстро уменьшается. Эта ситуация характерна для колебательного, но затухающего переходного процесса и учитывается базой правил. В случае критической ситуации, т.е. при возникновении автоколебаний, когда знак сигнала управляющего (корректирующего) воздействия НР совпадает со знаком скорости выходной переменной объекта, сигнал управляющего (корректирующего) воздействия НР должен обнуляться и оставаться ненулевым при противоположных знаках. Для критической ситуации оценку динамики переходного процесса можно получить, используя информацию об амплитуде отклонения регулируемой переменной от заданного значения (положительно большое или отрицательно большое).
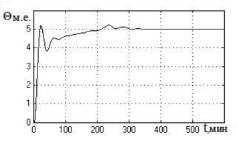
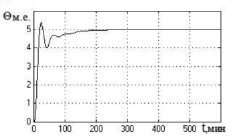
В установившемся режиме и при других параметрах модели объекта из интервала неопределенности система работает с прежней базой правил, обеспечивая оптимальное соотношение между временем регулирования, максимальной динамической ошибкой и количеством колебаний. Это подтверждается полученными переходными процессами при различных параметрах интервального объекта (рис. 4) и при подаче на вход регулятора и объекта ступенчатых воздействий. Переходные процессы были исследованы для трех режимов:
режим 1 – переходный процесс при выводе объекта на установившийся режим при воздействии ступенчатого сигнала по заданию θзад = 5 м.е. в момент времени t = 0;
режим 2 – переходный процесс при выводе объекта на установившийся режим при воздействии ступенчатого сигнала по заданию θзад = 5 м.е. в момент времени t = 0 с и ступенчатого возмущения на входе объекта f = 10 м.е., действующего в момент времени t = 200 мин, демпфированного звеном c передаточной функцией W(p) = 0,2/(20p + 1) (поскольку мгновенные скачки в технологии отсутствуют);
режим 3 – переходный процесс при выводе объекта на установившийся режим при воздействии ступенчатого сигнала по заданию θзад = 5 м.е. и скачкообразного возмущения на входе объекта f = 10 м.е. в момент времени t = 0.
Графики переходных процессов представлены на рис. 4.
Из полученных процессов регулирования видно, что нечеткая система с переменной структурой исключает недопустимые автоколебания в системе (сохраняя при наихудшем значении запаздывания объекта τmax = 6 мин незначительные колебания регулируемой переменной в установившемся режиме).
Рис. 4. Графики переходных процессов в нечеткой САУ биореактором в режимах 1 и 2 (а, в, д) и режиме 3 (б, г, е) для модели объекта с параметрами: а, б – T1 = 18,36 мин; T22 = 104,74 мин2; K = 0,187; τ = 2,2 мин; в, г – T1 = 27,26 мин; T22 = 299,34 мин2; K = 0,128; τ = 6 мин; д, е – T1 = 41,56 мин; T22 = 625,72 мин2; K = 0,104; τ = 4 мин
Заключение
Разработанная структура САУ с минимальной базой правил нечеткого регулятора позволяет реализовывать робастную систему управления неопределенным и нестационарным биотехнологическим объектом с запаздыванием. При этом настройку НР целесообразно осуществлять с использованием номинальной математической модели объекта, параметры которой находятся усреднением их возможных значений в интервалах изменения. Анализ робастного качества управления целесообразно проводить с использованием модели объекта с наихудшим сочетанием параметров, значения которых принимаются из предельно возможных их изменений.
Выводы
К достоинствам разработанной нечеткой системы управления с переменной структурой, относящейся к категории интеллектуальных систем управления, можно отнести следующие возможности:
– реализовать любой требуемый для интервального объекта с запаздыванием нелинейный алгоритм управления, в том числе полученный на основе аппроксимации нелинейных характеристик с помощью сигмоидных функций;
— осуществлять настройку регулятора с аппроксимирующим управлением при неполном и неточном описании интервального объекта управления с запаздыванием при минимальной базе правил и количестве настроечных параметров;
– исключить предельные и резкие значения управлений при неопределенности параметров и возмущений и реализовать коррекцию, обеспечивающую робастность системы при нестабильности параметров объекта.
Построение системы управления на базе нечеткой логики является наиболее приемлемым вариантом построения САУ биотехнологическим объектом, а также другими объектами, аналогичными ему по динамическим и статическим свойствам.