Что такое рса ключ
Что такое RSA-ключ ЕГАИС?

Ключ RSA ЕГАИС – что это?
Представляет собой сертификат для защищенного соединения с единой платформой. Система необходима для передачи данных в безопасном режиме. Криптосистема позволяет пользоваться ключом шифрования только соответствующим зарегистрированным субъектам. Все данные зашифрованы от посторонних третьих лиц. РСА-ключ для ЕГАИС записывается на крипто-ключ на веб-ресурсе официального портала. Операция по записи зашифрованных данных предоставляется бесплатно.
В процессе осуществления профессиональной деятельности для каждого юридического подразделения необходимо получить собственный RSA-ключ для работы с использованием Рутокен в ЕГАИС. Перед тем как зарегистрировать соответствующие данные требуется удостовериться, что запущен аппаратный крипто-ключ той компании, для которой формируется сертификат РСА.
Что нужно для формирования ключа RSA ЕГАИС Рутокен
На начальной стадии пользователю потребуется зарегистрироваться на официальном ресурсе. После этого понадобится зайти в Личный кабинет с помощью уже имеющейся электронной подписи. В панели управления необходимо будет выбрать графу «Показать сертификат». После чего вы сможете увидеть все сертификационные материалы со сведениями о ваших точках с указанием всех идентификационных данных. Представленная информация необходима для записи специального RSA-ключа.
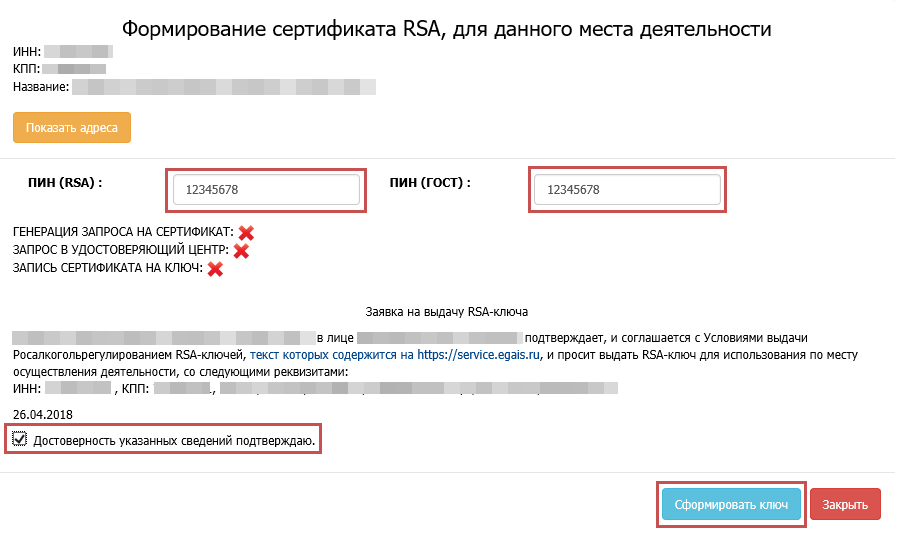
На следующем этапе нужно будет перейти в раздел «Получить ключ». На табло вы сможете увидеть перечень пунктов сбыта АП, которые были указаны вами при прохождении процедуры регистрации. Затем вы можете выбрать соответствующий пункт, для которого предназначен специализированный крипто-ключ и выбрать поле «Сформировать ключ». Электронная платформа запросит ввести пароль. В случае какого-либо затруднения вы можете обратиться в службу поддержки на официальном веб-ресурсе.
После того как вы установили или перезаписали РСА сертификат ЕГАИС на Рутокен можно приступать к установке УТМ. Запустив универсальный транспортный модуль, вы сможете приступить к производству и продаже алкоголя в рамках новых положений законодателя. Дополнительно нужно будет позаботиться о приобретении сканеров с целью считывания данных и стабильного осуществления всех процессов на электронной платформе.
Как обновить сертификат РСА ЕГАИС Рутокен
В связи с обновлением сертификата все субъекты алкорынка обязаны произвести обновление ключа RSA. В самом начале необходимо будет удалить старый сертификат и уже затем установить новый.
После удаления необходимо произвести обновление ключа RSA ЕГАИС Рутокен. Все манипуляции нужно будет выполнить на официальном веб-портале. При формировании ключа вам нужно будет ввести пин-код. Если все идентификационные данные будут введены правильно, сертификат будет зарегистрирован. В случае возникновения каких-либо сложностей при продлении ключа РСА ЕГАИС обратитесь в техподдержку. Специалисты могут подключиться удаленно к вашему компьютерному устройству в целях наиболее оперативного решения вопроса.
Ошибки с RSA-ключом ЕГАИС

Если же при обновлении ключа RSA ЕГАИС возникнут какие-либо сложности и не будет появляться графа «Запрос пин-кода», то необходимо в компьютерном оборудовании произвести соответствующие корректировки в настройках. В большинстве случаев неправильные настройки являются следствием невыполнения операций по формированию ключа.
При работе с использованием системы RuToken вам потребуется зайти в Панель управления, где потребуется выбрать Настройки, напротив строки Рутокен вам необходимо выбрать значение Microsoft Base Smart Card Crypto Provider. После этого нужно попробовать еще раз сформировать ключ. Если возникнут сложности, необходимо произвести обновление драйверов.
Помимо этого, проблема возникает при неправильном введении пин-кода. Если вы несколько раз неправильно ввели данные, то носитель может заблокироваться. Тогда вам придется обратиться в удостоверяющий центр. Дополнительно причиной ошибки может стать несоответствие адреса РСА ключа, указанного в лицензии. Если же будет выявление несоответствие данных, нужно будет обратиться в техподдержку Росалкогольрегулирования. С соответствующим запросом можно обратиться как лично, так и через Личный кабинет. Стоит отметить, что в некоторых случаях после внесения корректировок может потребоваться повторное формирование РСА-ключа.
Итак, для успешной работы во всероссийской системе вам помимо крипто-ключа и установки УТМ необходимо позаботиться о формировании RSA-ключа.
Что такое рса ключ
Генерация RSA-ключей на устаревших версиях Драйверов Рутокен может привести к проблемам с целостностью сертификатов на носителе.
Вход в личный кабинет ЕГАИС
Зайдите на сайт http://egais.ru/ (Internet Explorer 9.0 или выше) и перейдите по ссылке «Войти в личный кабинет».
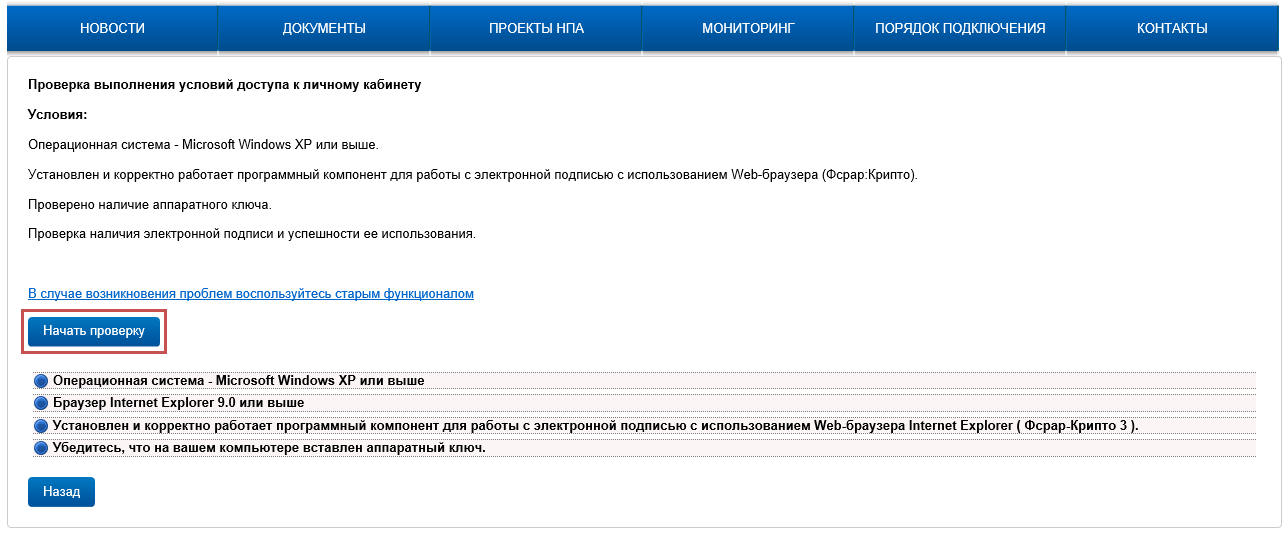
Нажмите кнопку «Ознакомиться с условиями и проверить их выполнение»
Проверьте, что Рутокен ЭЦП 2.0 вставлен и нажмите кнопку «Начать проверку»
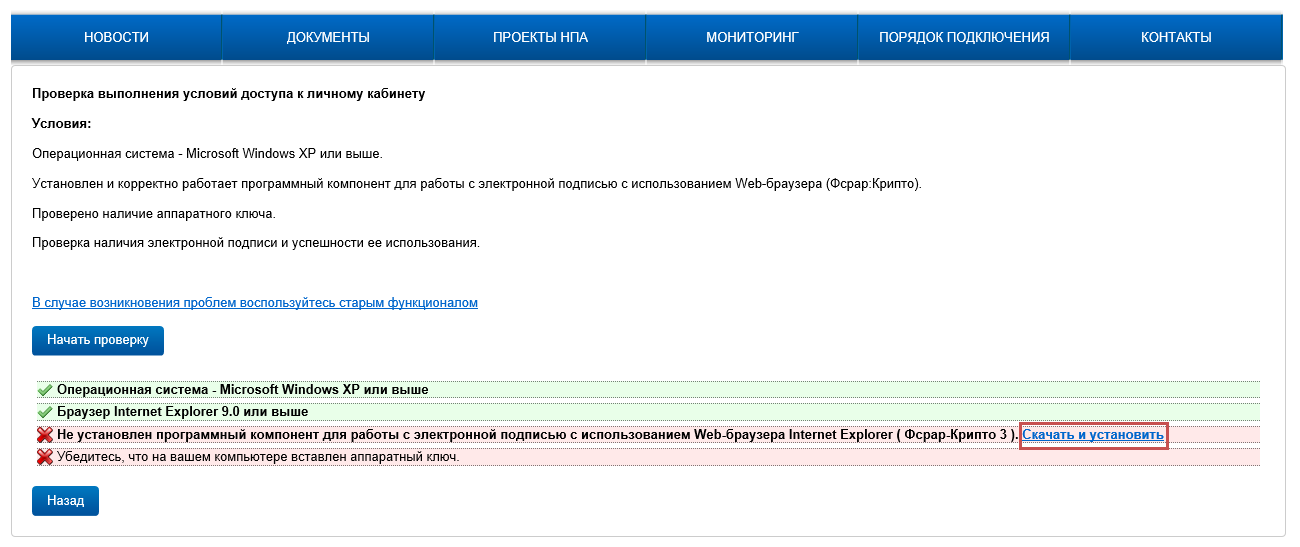
Если во время проверки выполнения условий для подключения к личному кабинету возникла ошибка «Не установлен программный компонент для работы с электронной подписью с использованием Web-браузера Internet Explorer (Фсрар-Крипто 3)«, выполните действия, указанные в инструкции ниже:
Скачайте и установите компонент «ФСРАР-Крипто 2».
Перед установкой ФСРАР Крипто 3 закройте все окна браузера Internet Explorer.
После успешной установки повторно зайдите на сайт http://egais.ru/ и повторно пройдите проверку выполнения условий доступа к личному кабинету.
Если ошибка сохранилась, воспользуйтесь рекомендациями, описанными в этой статье.
Если во время проверки выполнения условий для подключения к личному кабинету возникла «Не обнаружен аппаратный ключ. Перед следующей проверкой вставьте аппаратный ключ. (возможно не установлены драйверы аппаратного ключа, скачайте с сайта производителя аппаратного ключа)«, выполните действия, указанные в инструкции ниже:
— в USB-порт вставлен ключевой идентификатор модели Рутокен ЭЦП 2.0
— светодиод на ключе Рутокен ЭЦП 2.0 горит
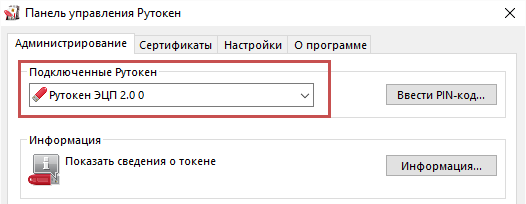
— ключевой идентификатор Рутокен определяется в «Панели управления Рутокен» в поле «Подключенные Рутокен»
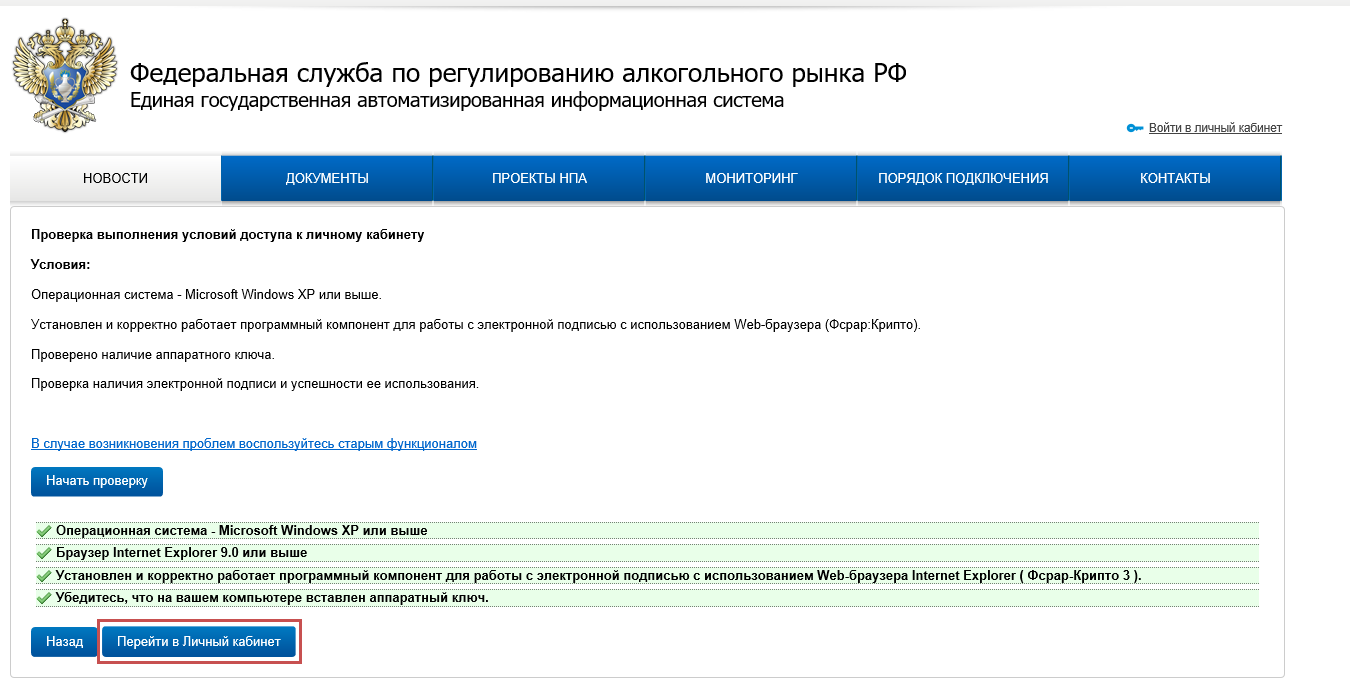
Проверка условий должна завершиться успехом.
Нажмите кнопку «Перейти в Личный кабинет».
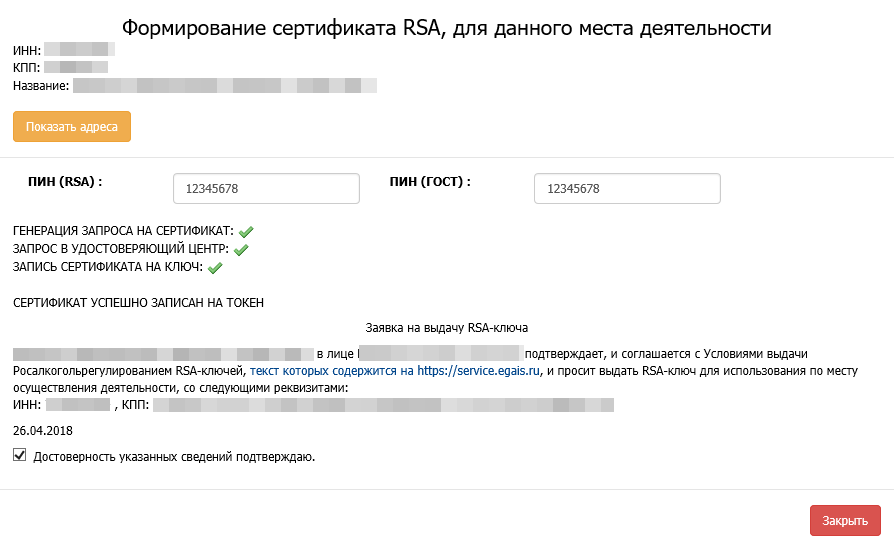
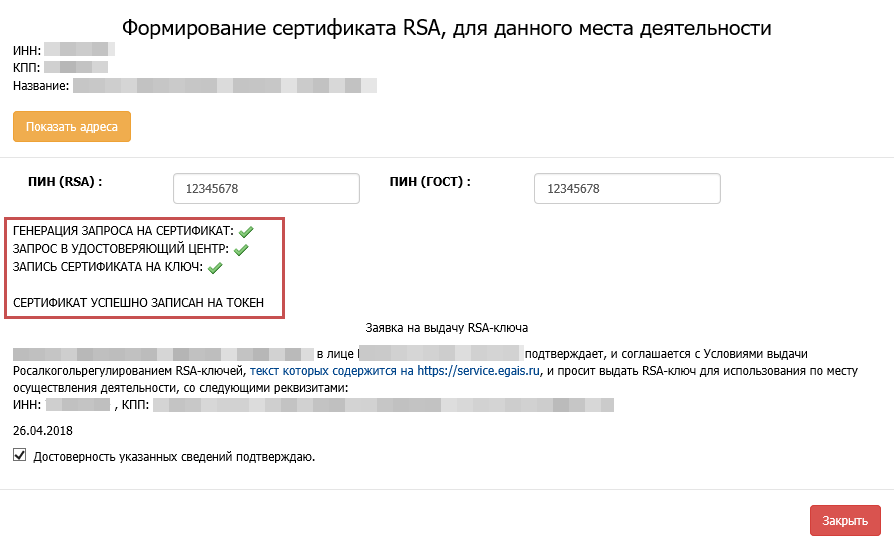
Получение RSA-ключа
RSA-ключ успешно записан на Рутокен ЭЦП 2.0.
Можно устанавливать Универсальный транспортный модуль.
Иллюстрация работы RSA на примере
Вокруг алгоритмов шифрования с отрытым и закрытым ключом существует множество недопониманий и мистификаций. Здесь я хотел бы предельно коротко и наглядно, с конкретными числами и минимумом формул, показать, как это работает.
Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах.
Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надёжности канала передачи данных. Приступим.
Шаг первый. Подготовка ключей
Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ.
Теперь пара чисел
Шаг второй. Шифрование
Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться.
Шаг третий. Расшифровка
Я получил ваши данные ( E=10 ), и у меня имеется закрытый ключ
Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования.
Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение ( E=10 ), так как ни у кого нет закрытого ключа.
В чём гарантия надёжности шифрования
Постараюсь это показать на примере. Давайте разложим на множители число 360:
Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5
Давайте теперь возьмём число 361. Тут нам придётся помучиться.
При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время.
А как это всё работает на практике?
Многие читатели спрашивают, как всё это применяется на практике. Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются.
Сперва сгенерируем ключи с чуть бо́льшими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20.
Оттолкнёмся от пары простых чисел
Мы готовы к шифрованию. Переведём наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19.
Мы можем зашифровать каждое из этих чисел открытым ключом
Немного о сложностях
На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путём недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы.
Таким образом, злоумышленнику не придётся отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их.
Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую.
Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие.
На практике, в исходное сообщение специально добавляются случайные и бессмысленные буквы в начало. Чтобы даже по первому коду было невозможно ничего понять. Получатель просто отбрасывает начало сообщения.
То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква.
В реальной жизни всё ещё немного сложнее. Блоки, на которые бьётся сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только потом применяется само RSA-шифрование.
Получатель делает всё в обратном порядке: расшифровывает, «распутывает» блоки и отбрасывает ненужную информацию, добавленную просто для выравнивания (чтобы сообщение можно было разбить на целое число блоков).
Детали и принципы формирования блоков можно почитать тут. Я же в этой заметке хотел рассказать только про RSA. Надесь, удалось.
Что такое рса ключ
Криптосистема [math]\mathtt
Содержание
Реализация [ править ]
Алгоритм [math]\mathtt
Криптографические системы с открытым ключом используют так называемые односторонние функции.
| Определение: |
| Односторонняя функция (англ. one-way function) — математическая функция, которая легко вычисляется для любого входного значения, но задача нахождения аргумента по заданному значению функции относится к классу NP-полных задач. |
Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
Создание открытого и секретного ключей [ править ]
| Определение: |
| Случайное простое число (англ. random prime numbers) — в криптографии, простое число, содержащее в двоичной записи заданное количество битов. |
Передача ключей [ править ]
Шифрование [ править ]
Расшифрование [ править ]
Корректность схемы [math]\mathtt[/math] [ править ]
Действительно, для [math]\forall m \in \mathbb
Возможны два случая:
где второе тождество следует из теоремы Ферма.
[math]m^
\equiv m \pmod
[/math]
Таким образом, при всех [math]m[/math] выполняется равенство
[math]m^
[/math]
Аналогично можно показать, что:
[math]\forall m \in \mathbb Стойкость алгоритма основывается на сложности вычисления обратной функции к функции шифрования [math]e \cdot d \equiv 1 \pmod<\varphi(n)>,[/math] Система [math]\mathtt Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается. Алгоритм шифрования сеансового ключа выглядит следующим образом: Алгоритм [math]\mathtt При неправильной или неоптимальной реализации или использовании алгоритма возможны специальные криптографические атаки, такие как атаки на схемы с малой секретной экспонентой или на схемы с общим выбранным значением модуля. На момент выдачи патента срок действия патента составлял 17 лет. Срок действия патента истекал 21 сентября 2000 г., когда 6 сентября 2000 г. RSA Security опубликовала алгоритм в открытом доступе. Алгоритм RSA состоит из четырех этапов: ключ поколения, распределение ключей, шифрования и дешифрования. Кроме того, для некоторых операций удобно, что порядок двух возведений в степень может быть изменен, и что это соотношение также подразумевает: Ключи для алгоритма RSA генерируются следующим образом: После того, как Боб получит открытый ключ Алисы, он может отправить сообщение M Алисе. Для расшифровки c = 2790 вычисляем Практические реализации используют китайскую теорему об остатках для ускорения вычислений с использованием модуля факторов (mod pq, используя mod p и mod q ). Предположим, Алиса использует открытый ключ Боба, чтобы отправить ему зашифрованное сообщение. В сообщении она может заявить, что она Алиса, но Боб не имеет возможности проверить, что сообщение было от Алисы, поскольку любой может использовать открытый ключ Боба для отправки ему зашифрованных сообщений. Чтобы проверить источник сообщения, RSA также может использоваться для подписи сообщения. Предположим, Алиса хочет отправить Бобу подписанное сообщение. Для этого она может использовать свой собственный закрытый ключ. Она создает хеш-значение сообщения, возводит его в степень d (по модулю n ) (как она это делает при расшифровке сообщения) и прикрепляет его как «подпись» к сообщению. Когда Боб получает подписанное сообщение, он использует тот же алгоритм хеширования в сочетании с открытым ключом Алисы. Он возводит подпись в степень e (по модулю n ) (как он это делает при шифровании сообщения) и сравнивает полученное хеш-значение с хеш-значением сообщения. Если они согласны, он знает, что автор сообщения владел закрытым ключом Алисы и что сообщение не подвергалось подделке с момента его отправки. Это работает из-за правил возведения в степень : час знак равно хэш ( м ) ; <\ displaystyle h = <\ text Таким образом, ключи можно менять местами без потери общности, то есть закрытый ключ пары ключей может использоваться либо для: Мы хотим показать, что ( м е ) d ≡ м ( мод п q ) <\ Displaystyle (м ^ <е>) ^ <д>\ экв м <\ pmod Проверка того, что m ed ≡ m (mod q ) проходит совершенно аналогично: Существует ряд атак на простой RSA, как описано ниже. Чтобы избежать этих проблем, практические реализации RSA обычно встраивают некоторую форму структурированного рандомизированного заполнения в значение m перед его шифрованием. Это заполнение гарантирует, что m не попадет в диапазон незащищенных открытых текстов и что данное сообщение после заполнения будет зашифровано одним из большого количества различных возможных зашифрованных текстов. Схемы безопасного заполнения, такие как RSA-PSS, столь же важны для безопасности подписи сообщений, как и для шифрования сообщений. Получены два патента США на PSS (USPTO 6266771 и USPTO 70360140); однако срок действия этих патентов истек 24 июля 2009 г. и 25 апреля 2010 г. соответственно. Использование PSS больше не ограничивается патентами. Обратите внимание, что использование разных пар ключей RSA для шифрования и подписи потенциально более безопасно. Эти значения позволяют получателю более эффективно вычислять возведение в степень m = c d (mod pq ) следующим образом: Это более эффективно, чем вычисление возведения в степень возведением в квадрат, даже если необходимо вычислить два модульных возведения в степень. Причина в том, что оба этих модульных возведения в степень используют меньший показатель степени и меньший модуль. Первая факторизация RSA-512 в 1999 г. использовала сотни компьютеров и потребовала 8 400 операций в секунду в год за время, примерно равное семи месяцам. К 2009 году Бенджамин Муди мог разложить ключ RSA-512 бит за 73 дня, используя только общедоступное программное обеспечение (GGNFS) и свой настольный компьютер (двухъядерный Athlon64 с процессором 1900 МГц). Требовалось менее пяти гигабайт дискового хранилища и около 2,5 гигабайт оперативной памяти для процесса просеивания. По состоянию на 2020 год самый большой общеизвестный факторный номер RSA составлял 829 бит (250 десятичных цифр, RSA-250 ). Его факторизация с помощью современной распределенной реализации заняла около 2700 процессорных лет. На практике ключи RSA обычно имеют длину от 1024 до 4096 бит. В 2003 году RSA Security подсчитала, что 1024-битные ключи, вероятно, станут поддающимися взлому к 2010 году. По состоянию на 2020 год неизвестно, могут ли такие ключи быть взломаны, но минимальные рекомендации перешли как минимум на 2048 бит. Обычно предполагается, что RSA безопасен, если n достаточно велико, вне квантовых вычислений. Нахождение больших простых чисел p и q обычно осуществляется путем проверки случайных чисел правильного размера с помощью вероятностных тестов на простоту, которые быстро исключают практически все непростые числа. Хенингер говорит в своем блоге, что плохие ключи почти полностью возникли во встроенных приложениях, включая «межсетевые экраны, маршрутизаторы, устройства VPN, устройства удаленного администрирования серверов, принтеры, проекторы и телефоны VOIP» от более чем 30 производителей. Хенингер объясняет, что проблема одного общего простого числа, обнаруженная двумя группами, является результатом ситуаций, когда генератор псевдослучайных чисел изначально плохо загружается, а затем повторно заполняется между генерацией первого и второго простых чисел. Проблему должно решить использование семян с достаточно высокой энтропией, полученных из таймингов нажатия клавиш, шума электронных диодов или атмосферного шума от радиоприемника, настроенного между станциями. Генерация сильных случайных чисел важна на всех этапах криптографии с открытым ключом. Например, если для симметричных ключей, распространяемых RSA, используется слабый генератор, то перехватчик может обойти RSA и напрямую угадать симметричные ключи. Была описана атака по побочному каналу с использованием анализа предсказания ветвлений (BPA). Многие процессоры используют предсказатель ветвления, чтобы определить, вероятно ли выполнение условного перехода в потоке команд программы. Часто эти процессоры также реализуют одновременную многопоточность (SMT). Атаки анализа предсказания ветвления используют шпионский процесс для обнаружения (статистически) закрытого ключа при обработке этими процессорами. Simple Branch Prediction Analysis (SBPA) утверждает, что улучшает BPA нестатистическим способом. В своей статье «О силе простого анализа прогнозирования ветвлений» авторы SBPA (Онур Ачиичмез и Цетин Кая Коч) утверждают, что за 10 итераций обнаружили 508 из 512 бит ключа RSA. Атака сбоя питания на реализации RSA была описана в 2010 году. Автор восстановил ключ, изменив напряжение питания процессора вне пределов; это вызвало несколько сбоев питания на сервере. Некоторые криптографические библиотеки, обеспечивающие поддержку RSA, включают:[math]\triangleleft[/math] Криптографическая стойкость [ править ]
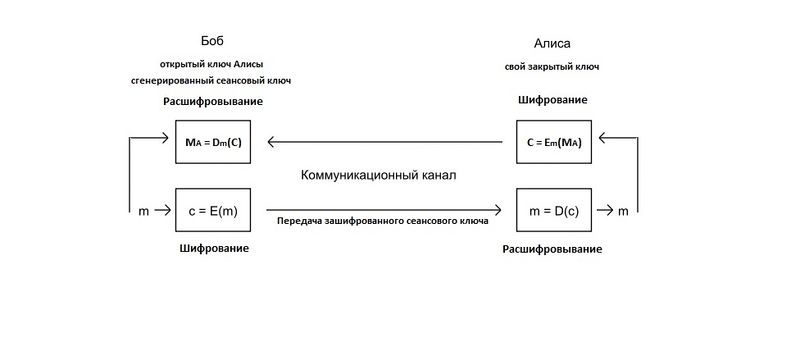
Применение [ править ]
Шифрование [ править ]
Расшифрование [ править ]
Минусы [ править ]
СОДЕРЖАНИЕ
История
Патент
Операция
Генерация ключей
Распределение ключей
Шифрование
Расшифровка
Пример
Подписание сообщений

Доказательства правильности
Доказательство с помощью малой теоремы Ферма.
Доказательство с использованием теоремы Эйлера.
Обивка
Атаки на простой RSA
Схемы заполнения
Безопасность и практические соображения
Использование китайского алгоритма остатка
Целочисленная факторизация и проблема RSA
Неправильная генерация ключей
Важность сильной генерации случайных чисел
Сроки атаки
Адаптивные атаки по выбранному зашифрованному тексту
Атаки анализа побочного канала
Реализации