Что такое ряды предпочтительных чисел
Что такое ряды предпочтительных чисел
ГОСТ 8032-84
(СТ СЭВ 3961-83)
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПРЕДПОЧТИТЕЛЬНЫЕ ЧИСЛА
И РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
Preferred numbers and series of preferred numbers
Дата введения 1985-07-01
Постановлением Государственного комитета СССР по стандартам от 9 августа 1984 г. N 2828 срок введения установлен с 01.07.85
ПЕРЕИЗДАНИЕ. Январь 1993 г.
Стандарт не распространяется на параметры технических объектов, естественная закономерность изменения значений которых отличается от закономерностей образования рядов, установленных настоящим стандартом.
Настоящий стандарт полностью соответствует СТ СЭВ 3961-83.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
(знаменатель прогрессии 
Значение определяет число членов прогрессии в одном десятичном интервале.
Предпочтительные числа представляют собой округленные значения членов ряда данной прогрессии.
Члены прогрессии, расположенные в интервале от 1,00 до 10,00 составляют исходный ряд.
1.2. Ряды предпочтительных чисел не ограничиваются в обоих направлениях, при этом предпочтительные числа менее 1 и более 10 получают делением или умножением членов исходного ряда на число 10, 100, 1000 и т.д.
1.3. Предпочтительные числа одного ряда могут быть либо только положительными, либо только отрицательными.
1.4. Свойства рядов предпочтительных чисел приведены в приложении 1.
2. ОСНОВНЫЕ РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
Ряды предпочтительных чисел (в технике)
Из Википедии — свободной энциклопедии
Ряды предпочтительных чисел (в технике) — это упорядоченная последовательность чисел, предназначенная для унификации значений технических параметров.
Ряды предпочтительных чисел создаются на основе числовых последовательностей. Это могут быть:
Арифметическим рядам свойственна относительная неравномерность расположения соседних членов: старшие члены ряда расположены относительно ближе, чем младшие. У геометрических прогрессий этот недостаток отсутствует, и поэтому они применяются чаще.
Каждый ряд содержит в каждом десятичном интервале соответственно 5, 10, 20 и 40 различных чисел. Более редкий ряд всегда является предпочтительным по отношению к более частому. Значения часто используемых первых четырех рядов в порядке их предпочтения:
Члены этих рядов по сравнению с точными значениями округлены в пределах 1,3 %. Предпочтительные числа других десятичных порядков получают умножением или делением на 10, 100 и т. д.
В электротехнике применяют ряды E, рекомендованные МЭК ИСО, со знаменателем геометрической прогрессии q= 10 k <\displaystyle <\sqrt[
Рекомендации по использованию нормальных линейных размеров не распространяется:
Что такое ряды предпочтительных чисел
Колчков В.И. МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ. М.:Учебное пособие
2. Стандартизация
2.3. Методические основы стандартизации
2.3.2. Система предпочтительных чисел
Размеры деталей и соединений, ряды допусков, посадок и другие геометрические параметры изделий, а так же параметры, отражающие функциональные свойства сборочных единиц, механизмов и машин общетехнического применения (подшипники качения, редукторы, электродвигатели и др.), целесообразно упорядочить и делать общими для всех отраслей промышленности, где эти изделия применяются. Применение упорядоченных чисел, представляющих собой ряды предпочтительных чисел, позволяет сократить номенклатуру типоразмеров изделий, создать условия для взаимозаменяемости, широкой унификации деталей и узлов и способствовать агрегатированию, а так же выбирать рациональные параметры процессов производства.
Применение рядов предпочтительных чисел представляет собой параметрическую стандартизацию, которая позволяет получить значительный эффект на всех стадиях жизненного цикла изделий ( проектирование, изготовление, эксплуатация и др.) Стандартами параметров охватывается большой диапазон характеристик изделий: материалы, заготовки, размерный режущий инструмент, оснастка, контрольные калибры, узлы по присоединительным размерам, выходные параметры электродвигателей и многое другое, что используется в той или иной отрасли промышленности.
Ряды предпочтительных чисел, применяемые в стандартизации, строятся на базе математических закономерностей. Наибольшее распространение получили ряды предпочтительных чисел представленные в ГОСТ 8032-84, который разработан на основе рекомендаций ИСО.
Стандартом установлены четыре основных десятичных ряда предпочтительных чисел R5, R10, R20, R40. В технически обоснованных случаях допускается применение двух дополнительных рядов R80 и R160. Ряды построены по правилу геометрической прогрессии со знаменателем равным корню из 10 степеней 5, 10, 20 и 40 соответственно.
Основанием этих рядов является число, состоящее из цифр 1 и 0, таким образом, они являются бесконечными как в сторону малых, так и в сторону больших значений, то есть допускают неограниченное представление чисел в направлении увеличения или уменьшения. Номер ряда предпочтительных чисел указывает на количество членов ряда в десятичном интервале, например, свыше 1 до 10 включительно. Число 1,00 не входит в десятичный интервал как завершающее число предыдущего десятичного интервала, т.е. свыше 0,10 до 1,00 включительно.
Допускается образование специальных рядов путем отбора каждого второго, третьего или n-го числа из существующего ряда. Так образуется ряд R10/3, состоящий из каждого третьего значения основного ряда, причем начинаться он может с первого, второго или третьего значения, например: R10/3 может состоять из чисел 1,00; 2,00; 4,00; 8,00 или R10/3 1,25; 2,50; 5,00; 10,00 или R10/3 1,60; 3,15; 6,30; 12,50. Можно составлять специальные ряды с разными знаменателями геометрической прогрессии в различных интервалах ряда.
Ряды предпочтительных чисел имеют ряд свойств, наличием которых объяснятся их широкое применение в стандартизации. Эти свойства позволяют переходить от стандартизации линейных величин к площадям, объёмам, энергетическим параметрам (производительности, мощности и др.).
Наиболее значимые из свойств рядов следующие: 1) Каждый последующий ряд содержит числа предыдущего ряда. 2) Произведение 2-х чисел рядов является числом, содержащимся в рядах, т.е. предпочтительным, что позволяет стандартизовать площади. 3) Произведение 3-х чисел ряда является числом, содержащимся в рядах, т.е. предпочтительным, что позволяет стандартизовать объёмы. 4) Начиная с ряда R10, в рядах содержится число 3,15 близкое к числу Пи, что позволяет стандартизовать длину окружностей, площадь кругов и объём цилиндров. 5) Произведение или частное любых членов ряда является, с учётом правил округления, членом ряда. Это свойство используется при увязке между собой стандартизованных параметров в пределах одного ряда предпочтительных чисел.
Согласованность параметров является важным критерием качественной разработки стандартов. В радиоэлектронике применяют предпочтительные числа с другими знаменателями геометрической прогрессии и образуют ряды Е, установленные Международной электротехнической комиссией (МЭК). При стандартизации иногда применяют ряды предпочтительных чисел, построенные по арифметической прогрессии. Арифметическая прогрессия положена в основу образования рядов размеров, например, в строительных стандартах. Встречаются ступенчато-арифметические ряды, у которых на отдельных отрезках прогрессии разности между соседними членами различны.
Ряды предпочтительных чисел (ГОСТ 8032-84)
Предпочтительными числами называются такие числа, которым отдается предпочтение по сравнению с другими.
Примеры использования предпочтительных чисел встречаются повсюду: размеры одежды и обуви, длина гвоздей, диаметр резьбы, номинальные значения масс гирь, мощность электрических машин, двигателей внутреннего сгорания и т. д.
Результатом использования предпочтительных чисел является такое согласование параметров и размеров, которое обеспечивает взаимозаменяемость деталей и узлов, создает предпосылки для гибких производственных систем, механизации и автоматизации производства, повышения производительности труда и в конечном итоге – повышения качества продукции.
Предпочтительным числам свойственны определенные математические закономерности. Наиболее простые ряды чисел строятся на основе арифметической прогрессии, в которой разность между последующим и предыдущим членами остается постоянной. Ряды, основанные на арифметической прогрессии, применяются сравнительно редко: ряд диаметров внутренних колец подшипников качения (через 5 мм), стандарты на размеры обуви. Преимуществом таких рядов является простота, а недостатком – относительная неравномерность. Например, в ряде из 100 членов разность – единица, но второй член относительно первого отличается на 100 %, десятый относительно девятого – на 11 %, а сотый относительно девяносто девятого – на 1 %. Таким образом, больших значений оказывается больше, чем маленьких, что не вполне соответствует потребностям.
Для преодоления этого недостатка может применяться ступенчатая арифметическая прогрессия, но гораздо чаще применяется геометрическая прогрессия, которая имеет важные преимущества:
1) постоянная относительная разность между любыми соседними членами ряда;
2) произведение или частное от деления любых двух членов прогрессии является новым членом ряда той же прогрессии.
Современный ряд предпочтительных чисел основан на геометрической прогрессии, которую в 1877 – 1879 гг. применил офицер французского инженерного корпуса Шарль Ренар при конструировании воздушных шаров. Ренар взял за основу канат имеющий массу а в граммах на 1 метр длины, и построил ряд, приняв знаменатель прогрессии, обеспечивающий десятикратное увеличение каждого пятого члена ряда, т. е. a g 5 = 10 a, откуда g = 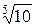
Труд Ренара был опубликован в 1886 г., но тогда не привлек к себе внимания. Только в 1910 г. (Германия), 1912 г. (Франции) были утверждены стандарты по этим рядам.
По ГОСТ 8032-84 установлено четыре основных и два дополнительных ряда:
R5 → 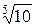
R10 → 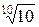
R20 → 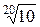
R40 → 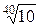
R80 → 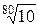
R160 → 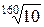
На основе рядов предпочтительных чисел определены значения нормальных линейных размеров (ГОСТ 6636-69), из числа которых выбираются номинальные величины. Номинальным размером называется такой, значение которого определяется любым видом расчета и округляется в соответствии с ГОСТ 6636-69. Номинальный размер затем проставляется на чертеже в качестве основного.
ТЕМА 7: РЯДЫ ПРЕДПОЧТИТЕЛЬНЫХ ЧИСЕЛ
Основой нормализации являются ряды чисел, подчиняющихся определенным закономерностям. В арифметических рядах каждый член образуется прибавлением к предыдущему члену постоянного числа (разность прогрессии) τ.
Величина любого члена ряда ак = а0 + kτ, где k — порядковый номер члена; а0 — первый член ряда, которому присваивается нулевой номер.
Рисунок 11 – Арифметические (а) и геометрические (б) ряды;
k – порядковый номер члена ряда
Арифметические ряды отличаются относительной неравномерностью. Их верхние области больше насыщены градациями размеров, а нижние меньше. Отношение каждого члена ряда к предыдущему имеет большую величину для первых членов ряда и резко уменьшается в верхних областях ряда.
С уменьшением j интервалы между членами ряда уменьшаются, число членов ряда возрастает; ряд получается более дробным (рис. 11, б).
| R | 5: | 1; 1,6; 2,5; 4; 6,3; 10. |
| R | 10: | 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10. |
| R | 20: | 1; 1,12; 1,25; 1,4; 1,6; 1,8; 2; 2,24; 2,5; 2,8; 3,15; 3,55; 4; 4,5; 5; 5,6; 6,3; 7,1; 8; 9; 10. |
| R | 40: | 1; 1,06; 1,12; 1,18; 1,25; 1,32; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2; 2,12; 2,24; 2,36; 2,5; 2,65; 2,8; 3; 3,15; 3,35; 3,55; 3,75; 4; 4,25; 4,5; 4,75; 5; 5,3; 5,6; 6; 6,3; 6,7; 7,1; 7,5; 8; 8,5; 9; 9.5; 10. |
большим округлением чисел по сравнению с основными. В отличие от основных ряды нормальных размеров обозначают буквой а:
ГОСТ 6636-69 охватывает линейные размеры в интервале 0,001 — 20000 мм.
Применение тестированных линейных размеров целесообразно для поверхностей, подвергаемых точной механической обработке, особенно для диаметров посадочных соединений, что способствует нормализации режущего, контрольного и мерительного инструмента и облегчает настройку станков.
Главный экономический выигрыш получается при сокращении числа членов рядов, т. е. при применении в каждом отдельном случае наиболее низкого ряда, обеспечивающего нужный диапазон размеров.
Меньшее значение имеют нормальные размеры для поверхностей, не нуждающихся в точной координации.
На основании нормальных линейных размеров устанавливают ряды диаметров проволоки, прутков, толщины листового проката, линейных размеров сечений фасонного проката.
Применять нормализованные ряды для осевых размеров и для размеров необрабатываемых поверхностей (литье, штамповка) нерационально. В таких случаях даже частичная нормализация размеров, не давая никаких реальных преимуществ, только усложняет процесс проектирования и изготовления деталей,
Ряды предпочтительных чисел в конструировании. Значение рядов предпочтительных чисел для конструирования не следует переоценивать. Некоторые конструкторы считают необходимым применять ряды предпочтительных чисел для нормализации и для всех областей конструирования. Это неверно.
Ряды предпочтительных чисел целесообразно использовать в случаях, когда требуется создавать ряд градаций какого-либо параметра с равномерной насыщенностью градаций во всех частях ряда (например, передаточных отношений в коробках передач и подач металлорежущих станков).
Однако равномерное распределение градаций не всегда является наиболее рациональным. Правильнее при нормировании технических параметров исходить из плотности распределения применяемости данного параметра.
Рисунок 12 – Применяемость модулей зубьев
В качестве примера на рис. 12 приведен график применяемости модулей зубьев в общем машиностроении. Как видно, 90% всех применяемых колес имеют модуль в пределах т = 1 ¸ 5.
Ряды предпочтительных чисел неприменимы для создания унифицированных рядов машин с повторяющимися рабочими органами. Параметры унифицированных рядов складываются по другим законам, зависящим от реальных возможностей сочетания унифицированных органов и условий технической применяемости членов ряда, и не могут уложиться в геометрическую прогрессию.
Параметрические ряды необходимо строить с учетом применяемости различных категорий машин, степени их гибкости и т. д. Формальное применение геометрических прогрессий может привести к большим ошибкам.
Неприменимы ряды предпочтительных чисел и для: определения параметров прогрессивно развиваемых и модернизируемых машин, параметры которых на каждой стадии зависят от технических возможностей и потребностей соответствующих отраслей народного хозяйства. Так, мощность тепловых машин зависит от их начальных параметров (давления и температуры) и частоты вращения. Ни один из этих параметров невозможно произвольно увеличить. В некоторых случаях они имеют оптимальное значение (например, степень сжатия в газовых турбинах), изменение которого ухудшает показатели машины. Увеличение температуры и частоты вращения возможно только на базе технических усовершенствований (повышения жаропрочности материалов, улучшения охлаждения термически напряженных деталей). Результаты этих поисковых работ невозможно уложить в ряды предпочтительных чисел.
Общий вывод состоит в том, что параметры нормализуемых элементов следует выбирать не на основе априорных закономерностей, а исходя из конкретных условий их применяемости.


