Что такое с недостатком и с избытком
Что такое с недостатком и с избытком
Автор: Додонов Вячеслав Григорьевич
Организация: МОУ Ново-Томышевская основная школа
Населенный пункт: Ульяновская область, с. Новое Томышево
Класс: 5
Предмет: МАТЕМАТИКА
Тип урока: Урок изучения нового материала.
Цели урока:
— формировать умения и навыки определять расстояние между двумя точками;
— измерять длину отрезка с точностью до 1 см с недостатком, с избытком, с округлением;
Формировать УУД:
Личностные: способность к самооценке на основе критерия успешности учебной деятельности.
Регулятивные: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; оценивать правильность выполнения действия на уровне адекватной оценки; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать свое предположение.
Коммуникативные: умение оформлять свои мысли в устной и письменной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им; планирование сотрудничества с учителем и одноклассниками в поиске и выборе информации; слушать и понимать речь других; построение логической цепи рассуждений, выдвижение гипотез и их обоснование.
Познавательные: умение ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя); добывать новые знания (находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке)
Планируемые результаты
Коммуникативные: формировать умения учащихся воспроизводить мысли устной и письменной речью;
Регулятивные: анализировать, сравнивать, обобщать и делать выводы, выступать перед аудиторией.
Личностные: способность к самоуправлению, сознательную дисциплину, трудолюбие, усидчивость, самостоятельность в работе.
Предметные: знать единицы измерения отрезков, понятие приближённой длины отрезка с недостатком, с избытком, с округлением.
Оборудование: ноутбук, презентация.
Мы сегодня продолжим работать по теме «Измерение отрезков». Поэтому давайте вспомним понятия, с которыми познакомились на прошлом уроке (слайд 1):
— Расшифруйте предложенные термины: плоскость, прямая, луч, отрезок.
— Скажите, что из перечисленного мы сможем измерить?
— Чем?
— Как называется отрезок, длина которого принята за единицу измерения?
— Что называют расстоянием между двумя точками?
— Расскажите, как мне с помощью линейки измерить отрезок?
— Посмотрим небольшой сюжет (демонстрация фрагмента мультфильма «38 попугаев»): https://yandex.ru/video/preview/?text=мультфильм%2038%20попугаев%20измерение%20удава&path=wizard&parent-reqid=1616507733142502-441565576134106352500121-production-app-host-vla-web-yp-38&wiz_type=vital&filmId=4340551432591760197
— Какой значение имеет этот сюжет к нашей теме?
— Удалось ли друзьям удава точно измерить его длину?
Цель: Обеспечение мотивации учения детьми, принятие ими темы и целей урока.\
Мы сейчас с вами проведем небольшое исследование и попытаемся ответить на вопросы (слайд 3):
Понятно, что каждый отрезок имеет определенную длину, но длина не всякого отрезка в точности равна целому числу единичных отрезков, которыми он измеряется.
В этом случае точная длина отрезка АВ осталась неизвестной.
Однако известно, что 5 см
Знак ≈ называют знаком приближенного равенства и читают «приближенно равно».
В рассмотренном примере длина отрезка АВ приближенно равна 5 см с недостатком и 6 см с избытком с точностью до 1 см.
Однако ещё можно получить приближённую длину отрезка с точностью до 1 см с округлением. Поясним эти слова.
Т.к. точка В расположена ближе к делению 5, то более точным приближением длины отрезка АВ является 5 см. В таком случае говорят, что длина отрезка АВ приближённо равна 5 см с округлением с точностью до 1 см.
Если же точка В оказалась бы ближе к делению 6, то мы сказали бы, что длина отрезка АВ приближённо равна 6 см с округлением с точностью до 1 см.
Остается ещё третий случай, когда точка В окажется точно посередине между делениями линейки 5 и 6. В этом случае условились считать, что 6 см есть приближенная длина отрезка АВ с точностью до 1 см с округлением.
5. Закрепление изученного материала.
Цель: Выявить качество и уровень усвоения знаний, а также установить причины выявленных ошибок.
Задание (слайд 4): Найдите приближенно длину отрезка (у доски работают 2 ученика):
6. Физминутка.
Цель: сменить вид деятельности.
Давайте немного отдохнем.
Поднимает руки класс – это «раз».
Повернулась голова – это «два».
Руки вниз, вперед смотри – это «три».
Руки в стороны пошире развернули на «четыре»,
С силой их к плечам прижать – это «пять».
Всем ребятам надо сесть – это «шесть».
Задание (слайд 5): Найдите и запишите длину отрезков округлением. (самостоятельно в тетрадях с последующей проверкой),
Задание (слайд 6): № 374 (соревнования между рядами).
7. Самостоятельная работа (слайд 7):
8. Рефлексия (слайд 8):
Цель: оценить результаты собственной деятельности.
— Итак, над какой темой урока мы сегодня с вами работали?
— Как происходить округление с избытком; недостатком.
— Как найти длину отрезка округлением?
9. Домашнее задание (слайд 9):
п. 2.2., стр. 81-82, учить определения,
№ 374, № 377 на стр. 83 выполнить в тетрадях.
10. Подвести итог урока. Оценить работу класса. Выставить оценки учащимся.
Что такое с недостатком и с избытком
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В жизни человека встречается два вида чисел: точные и приближённые.
Например, у квадрата четыре стороны, число 4 является точным.
Другая ситуация, на вопрос, сколько вам лет вы отвечаете 12, это приближенная величина, мы ведь не говорим 12 лет 7 месяцев 26 дней.
На практике мы часто не знаем точных значений величин. Никакие весы, как бы хорошо они ни были настроены, не могут показать абсолютно точный вес. Любой термометр показывает температуру с той или иной погрешностью. Наш глаз не в состоянии увидеть четко показания прибора, поэтому вместо того, чтобы иметь дело с точным значением величины, мы вынуждены оперировать с ее приближённым значением
Однако знание о приближённом числе уже даёт понимание о сути дела, и к тому же не всегда точное значение бывает необходимо.
Приближенные значения чисел в математике разделяют на:
1. приближенные значения с избытком;
2. приближенные значения с недостатком.
Например, про арбуз, который весит 9 кг 280 г, мы можем сказать, что его вес примерно равен 9 кг. Это приближенное значение с недостатком. А если бы его вес составлял 9 кг 980 грамм, мы бы сказали 10 кг – это приближенное значение с избытком.
Давайте рассмотрим такие примеры:
1)число 58,79 больше чем 58, но меньше 59. Число 58,79 ближе расположено к натуральному числу 59;
2)число 181, 123 больше, чем 181, но меньше, чем 182. Число 181,123 расположено ближе к натуральному числу 181. То натуральное число, к которому дробь ближе называют округленным значением этого числа.
Под округлением числа понимают отбрасывание одной или нескольких цифр в десятичном представлении числа. Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Например, число 58,79 округляется до 59, так как число 59 расположено ближе, а число 181,123 округляется до 181.
А что делать, если расстояния до приближенного значения числа с недостатком и избытком равны, например, 23,5? Оказывается, округляют в большую сторону! Т.е. получится 24
Наверняка у вас возник вопрос: «А можно ли округлять не до целого?» Конечно! Округлять можно и до других разрядов, например, до десятых, сотых, тысячных или же до десятков, сотен, тысяч и так далее.
Существует четкое правило для округления чисел:
Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения. Если за подчеркнутой цифрой стоит цифра 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличиваем на 1.
Теперь стало понятно, почему число 23,5 округлили до 24.
Т.к. отбрасываемая цифра равна 5.
Округлим число 86,275 до десятых.
Подчеркнем цифру 2, отбрасываем цифры 7 и 5, которые следуют за разрядом десятых. За подчеркнутой цифрой 2 стоит цифра 7, поэтому цифру 2 увеличиваем на 1. Получаем 86,3. Записывают это так:
Округлим число 6,6739 до сотых.
Подчеркиваем цифру 7, отбрасываем цифры 3 и 9, которые следуют за разрядом сотых. За подчеркнутой цифрой 7 стоит цифра 3, поэтому цифру 7 оставляем без изменения. Получаем 6,67.
Записывают это так:
Таким образом, можно убедиться, что если десятичную дробь округляют до какого-нибудь разряда, то все следующие за этим разрядом цифры отбрасывают.
Округлим число 8 154 до сотен.
Подчеркиваем цифру 1, за ней следует цифра 5, значит 1 заменяем цифрой 2, а все последующие цифры нулями, то есть получится 8200.
Записывают это так:
Делаем вывод, что при округлении натурального числа до некоторого разряда все цифры последующих разрядов заменяются нулями.
Итак, перед вами несложный алгоритм, который позволяет правильно выполнить округление любого числа:
Первое: найти нужный разряд и подчеркнуть стоящую в нем цифру.
Второе: переписать все цифры, стоящие до нее.
Третье: заменить все цифры, стоящие после выделенной, нулями до конца целой части или отбросить все цифры, имеющиеся после выделенной, если они стоят после запятой.
Четвертое: увеличить выделенную цифру на единицу, если за этой цифрой стоит цифра 5,6,7,8,9 или переписать выделенную цифру без изменений, если за ней стоит цифра 0,1,2,3,4.
Таким образом, в ходе этого урока Вы узнали, что такое приближенные значения чисел с недостатком и избытком округление чисел, а также приобрели четкий алгоритм, который позволяет правильно выполнить округление любого числа!
Химия, Биология, подготовка к ГИА и ЕГЭ
Задачи такого типа (точнее, это может быть даже не самой задачей, а частью задачи) есть в части С ГИА, они входят в часть С ЕГЭ, теперь они появились и в части B.
Классический пример задачи на избыток и недостаток.
Этапы решения задачи:
1. Записываем уравнение реакции и уравниваем его:
2. Находим количество моль тех веществ, массы которых нам даны в условии:
n(Cu) = m\Ar =3.2 г \ 63.5 г\моль = 0,05 моль
m(Hg(NO3)2) = m\Mr = 20 \ 324 = 0,06 моль
3. Сравниваем количество моль веществ и определяем недостаток:
по уравнению реакции меди и нитрат ртути реагируют 1:1, значит, их количество моль тоже должно быть одинаковым
0,05 моль ПО НЕДОСТАТКУ
Почему по недостатку? Это аналогично вопросу — «сколько целых яблок можно сложить из 5 половинок? «
4. Вычисляем массу продукта по количеству моль, соответствующему недостатку:
0,05 моль ——> 0,05 моль
m(Hg)= n*Ar = 0,05 моль * 200 г\моль = 10 г
______________________________________________________________________________________
Пример задачи на избыток и недостаток,
где вещества в другом соотношении:
те же самые этапы решения:
1. Записываем уравнение реакции и уравниваем его:
2. Находим количество моль тех веществ, массы которых нам даны в условии:
n(N2 ) = m\Mr = 14\28=0.5 моль
3. Сравниваем количество моль веществ и определяем недостаток:
в этом уравнении все не так очевидно, как в предыдущем, поэтому нужно просто прикинуть:
4. Вычисляем массу продукта по количеству моль, соответствующему недостатку:
m(N2O5) = n*Mr = 2* 0.5\5 моль * 108 г\моль = 21 г
______________________________________________________________________________________
Есть задачи, очень похожие на задачи избыток-недостаток,
1. Записываем уравнение реакции и уравниваем его:
здесь у нас возможно 2 варианта — образование средней и кислой соли:
2. Находим количество моль тех веществ, массы которых нам даны в условии:
n(CO2 ) = V\22.4 л\моль = 24.9 \ 22.4 = 1,11 моль
n(NaOH)= m\Mr = 44.4\40 = 1,11 моль
т.к. количество моль веществ одинаково, то делаем вывод, что реакция протекает по схеме образования кислой соли:
4. Вычисляем массу продукта по количеству моль:
m ( NaHCO3) = n*Mr = 1,11 * 84 = 93,24 г
_____________________________________________________________________________________ _
Задачи на избыток и недостаток не трудные, зачастую они являются частью более сложных задач, поэтому все, что нужно сделать, это натренироваться — порешать как можно больше таких примеров, внимательно уравнивая и работая с коэффициентами.
Методика решения задач
на «избыток–недостаток»
в курсе основной
общеобразовательной школы
Умение решать химические задачи – важная составляющая знаний по предмету. Согласно государственному стандарту образования по химии учащиеся, оканчивающие школу, должны уметь решать более десятка типов стандартных задач. Среди них и задачи на «избыток–недостаток».
Предлагаю свой вариант подачи материала по решению таких задач в курсе химии 9-го класса.
На изучение этой темы отвожу 2–2,5 урока, в зависимости от уровня способностей учеников класса. Ознакомление с алгоритмом решения задач данного типа происходит в рамках изучения темы «Теория электролитической диссоциации». Однако если класс сильный, то в рамках эксперимента этот тип задач иногда изучаем и в конце 8-го класса в главе «Галогены», а высвободившееся время можно потратить на изучение органической химии в курсе 9-го класса.
На первом уроке разбираю два типа задач на «избыток–недостаток»:


В качестве домашнего задания обязательно предлагаются две-три задачи, подобные изученным на уроке.
На втором уроке закрепляю и углубляю изученный материал, ввожу понятия «процентная концентрация растворов веществ», вступивших в реакцию, «плотность растворов». Кроме того, усложняю задачи, вводя «процентное содержание примесей в исходном веществе» и т. д. Такой прием позволяет повторить элементы уже изученного материала, сэкономить время. В конце второго урока изучения темы или в начале третьего провожу небольшую самостоятельную работу на закрепление изученного материала, включающую одну-две задачи, причем самостоятельная работа предлагается в трех уровнях сложности, в зависимости от способностей ученика.
Урок 1
Решение задач на «избыток–недостаток»
ХОД УРОКА

Решая химические задачи, следует не забывать о правилах их грамотного оформления по схеме: дано, найти, решение, ответ.
ЗАДАЧА 1. На 47 г оксида калия подействовали раствором, содержащим 40 г азотной кислоты. Найдите массу образовавшегося нитрата калия.
Решение
Рассчитаем относительные молекулярные массы интересующих нас веществ:
Для удобства расчета за х1 примем массу НNО3 и найдем, какое из веществ, вступивших в реакцию, дано в избытке, какое – в недостатке.
Следовательно, азотная кислота дана в недостатке, т. к. по условию ее 40 г, а по расчету необходимо 63 г, поэтому расчет ведем по HNO3:
ЗАДАЧА 2. На 24 г металлического магния подействовали 100 г 30%-го раствора соляной кислоты. Найдите массу образовавшегося хлорида магния.
m(Mg) = 24 г,
m(р-р HCl) = 100 г, 
Решение
Рассчитаем относительные молекулярные массы интересующих нас веществ:
Для удобства расчета за х1 примем массу соляной кислоты и найдем, какое из веществ, вступивших в реакцию, дано в избытке, какое – в недостатке.
Из расчета видно, что соляная кислота дана в недостатке, т. к. по условию задачи ее дано 30 г, а для реакции требуется 73 г. Следовательно, расчет ведем по соляной кислоте:

ЗАДАЧА 1. На 36 г алюминия подействовали 64 г серы. Найдите массу образовавшегося сульфида алюминия.
Решение
Примем массу Al за х1 и найдем, какое из веществ, вступивших в реакцию, дано в избытке, какое – в недостатке.
В данном случае вещества, вступившие в реакцию, взяты в стехиометрических количествах, поэтому расчет можно вести по любому из них:
ЗАДАЧА 2. На раствор, содержащий 53 г карбоната натрия, подействовали раствором, содержащим 49 г серной кислоты. Найдите массу образовавшейся соли.
Решение
Рассчитаем относительные молекулярные массы интересующих нас веществ:
Примем за х1 массу cерной кислоты, чтобы узнать, какое вещество дано в избытке, какое – в недостатке.
В данном случае оба вещества взяты в стехиометрических количествах, поэтому расчет можно вести по любому из них:
Однако учитель, подбирая задачи для решения в классе, должен помнить, что в некоторых случаях (например, если кислота или кислотный оксид дан в избытке) решение задачи не ограничивается расчетом двух пропорций, т. к. реакция будет протекать дальше с образованием кислой соли. Это повысит сложность материала. На первых уроках при решении задач данного типа я не включаю в материал задачи на прохождение реакций с образованием кислых или основных солей.
Домашнее задание
ЗАДАЧА 1. На 200 г 10%-го раствора серной кислоты подействовали 40 г оксида алюминия. Найдите массу образовавшейся воды.
M(р-р H2SO4) = 200 г, 
m(Al2O3) = 40 г.
Решение
Рассчитаем относительные молекулярные массы интересующих нас веществ:
Найдем, какое из вступивших в реакцию веществ дано в избытке, а какое – в недостатке.
Из расчета видно, что Al2O3 дан в избытке, следовательно, расчет ведем по кислоте:
ЗАДАЧА 2. На 40 г оксида меди(II) подействовали раствором серной кислоты, содержащим 49 г безводного вещества. Найдите массу образовавшейся соли.
Решение
Найдем, какое из веществ, вступивших в реакцию, дано в избытке, а какое – в недостатке.
Cогласно уравнению данной реакции вещества взяты в стехиометрических количествах, поэтому расчет можно вести по любому из них:
Что такое с недостатком и с избытком
Репетитор по химии и биологии
100 баллов ЕГЭ по химии!
Первый МГМУ им. И.М. Сеченова
выпускница репетитора В.Богуновой
РГМУ по химии 2010
РНИМУ им. Н.И. Пирогова
выпускница репетитора В.Богуновой
Первый МГМУ им. И.М. Сеченова
выпускница репетитора В.Богуновой
МГМСУ, лечебный факультет
выпускник репетитора В.Богуновой
МГМСУ, лечебный факультет
выпускница репетитора В. Богуновой
РНИМУ им. Н.И. Пирогова
выпускник репетитора В.Богуновой
Первый МГМУ им. И.М. Сеченова
выпускница репетитора В.Богуновой
Секретная шпаргалка по химии.
Вы хотите познавать химию и профессионально, и с удовольствием? Тогда вам сюда! Автор методики системно-аналитического изучения химии Богунова В.Г. раскрывает тайны решения задач, делится секретами мастерства при подготовке к ОГЭ, ЕГЭ, ДВИ и олимпиадам
В ряде задач представлены данные для обоих реагентов. Как в таких случаях выполнять расчеты по уравнения реакций? Что брать в качестве точки расчета? Давайте разбираться. Вначале определимся с понятиями.
Для того, чтобы понять, в каких соотношениях представлены количества веществ-реагентов в конкретной задаче, необходимо начать анализ задачи по уже известным Четырем Заповедям. После выполнения Предварительных Расчетов (Третья Заповедь), следует выписать количества веществ над формулами реагентов в уравнении реакции и произвести пересчет количества одного вещества через количество другого. После определения избытка-недостатка дальнейшие расчеты в задаче производим по недостатку.
Как определить избыток-недостаток и провести дальнейшие расчеты, лучше разобрать на конкретной задаче. Читайте внимательно и попробуйте записать решение задачи на отдельном листе бумаги.
На 47 г оксида калия подействовали раствором, содержащим 40 г азотной кислоты. Найдите массу образовавшегося нитрата калия.
1) Первая Заповедь. Выписать данные задачи в разделе «Дано».
2) Вторая Заповедь. Написать уравнение реакции.
Немного теории химии. Оксиды щелочных металлов проявляют ярко выраженные основные свойства. Они легко реагируют с кислотами с образованием солей.
3) Третья Заповедь. Сделать предварительные расчеты по данным условия задачи
На этой стадии необходимо определить, кто из реагентов в избытке, а кто в недостатке. Для этого следует провести пересчет количества одного вещества через количество другого. Покажу два способа пересчета и анализа. Можете пользоваться любым, какой понятней.
2) Считаем количество вещества оксида калия по количеству вещества азотной кислоты (обычный расчет по уравнению реакции). Я мысленно произношу: «Пусть вся азотная кислота вступила в реакцию. Сколько тогда прореагирует оксида калия?» Оксида калия, по расчетам, требуется меньше, чем дано, значит, оксид калия в избытке.
4) Четвертая заповедь. Составить алгоритм решения задачи.
Формулизируем вопрос задачи «Найдите массу образовавшегося нитрата калия», т.е. записываем формулу расчета массы, которая для нас, как для химиков, должна быть представлена произведением количества вещества на молярную массу.
Анализируем компоненты формулы: молярную массу нитрата калия определяем по таблице Менделеева, количество вещества нитрата калия рассчитываем по уравнению реакции исключительно по недостатку!
Смешали 7,3 г хлороводорода и 4 г аммиака. Какая масса соли при этом образуется?
Последовательность действия, выполняемых при решении задачи:
1 ) Выписать данные в разделе «Дано»
2) Написать уравнение реакции
3) Сделать предварительные расчеты
4) Определить избыток-недостаток
5) Сделать расчет по уравнению реакции (по недостатку!)
6) Составить алгоритм решения
7) Сделать окончательный расчет
На 36 г алюминия подействовали 64 г серы. Найдите массу образовавшегося сульфида алюминия.
При поджигании смеси порошкообразных алюминия и серы между ними начинается интенсивная экзотермическая реакция с образованием сульфида алюминия, который полностью гидролизуется водой, поэтому не может быть получен обменными реакциями в водных растворах.
Последовательность действия, выполняемых при решении задачи:
1) Выписать данные в разделе «Дано»
2) Написать уравнение реакции
3) Сделать предварительные расчеты.
4) Определить избыток-недостаток
5) Сделать расчет по уравнению реакции (по недостатку!)
6) Составить алгоритм решения
7) Сделать окончательный расчет
Секрет таланта и успеха на ЕГЭ
Вы готовитесь к ЕГЭ и хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии. Здесь вы найдете огромное количество задач, заданий и теоретического материала, познакомитесь с моими учениками, многие из которых уже давно работают врачами.



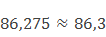
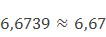
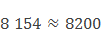



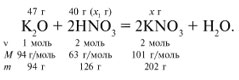
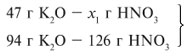
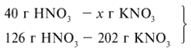
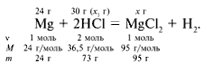
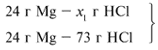
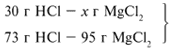
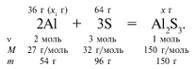
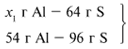
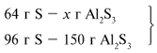
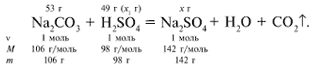
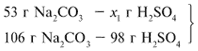
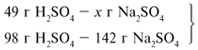
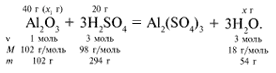
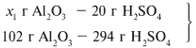
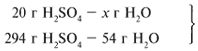
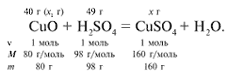
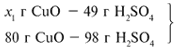





m.jpg)
m.jpg)
m.jpg)

m.jpg)
m.jpg)
m.jpg)
_1.jpg)
_2.jpg)
_3.jpg)