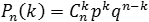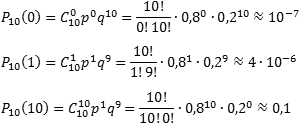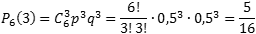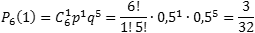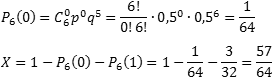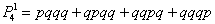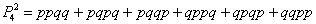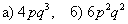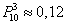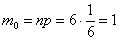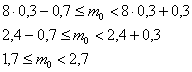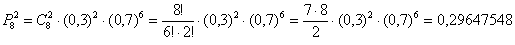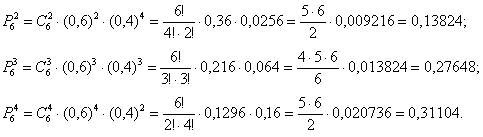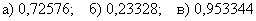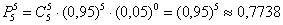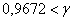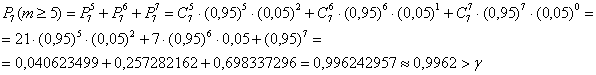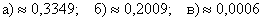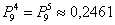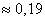Что такое с в формуле бернулли
Схема Бернулли. Примеры решения задач
Не будем долго размышлять о высоком — начнем сразу с определения.
Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.
Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:
Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.
Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:
. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:
где C n k — число сочетаний, q = 1 − p.
Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.
По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A », т.е. выпуск бракованного изделия.
Таким образом, имеем: n = 10; p = 0,8; q = 0,2.
Итак, находим вероятность того, что в партии все детали бракованные ( k = 0), что только одна деталь без брака ( k = 1), и что бракованных деталей нет вообще ( k = 10):
Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:
Таким образом, имеем: n = 6; p = 0,5; q = 0,5.
Определим вероятность того, что герб выпал три раза, т.е. k = 3:
Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:
Заметим, что эта сумма также равна (1 − P 6(0) − P 6(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз ( k = 1) или не выпал вообще ( k = 0). Поскольку P 6(1) нам уже известно, осталось найти P 6(0):
Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?
Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.
Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.
Найдем вероятность получить два «дефектных» телевизора ( k = 2) и три ( k = 3):
Очевидно, P 20(3) > P 20(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.
Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.
Учебник по теории вероятностей
1.7. Независимые испытания. Формула Бернулли
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
$$P_n(k)=C_n^k \cdot p^k \cdot q^
Распределение числа успехов (появлений события) носит название биномиального распределения.
Онлайн-калькуляторы для формулы Бернулли
Некоторые наиболее популярные типы задач, в которых используется формула Бернулли, разобраны в статьях и снабжены онлайн-калькулятором, вы можете перейти к ним по ссылкам:
Примеры задач с решениями
Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности 

По формуле Бернулли требуемая вероятность равна 
Пример. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение. Вероятность рождения девочки 

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:




Следовательно, искомая вероятность

Пример. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Пример. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Решение. Вычисляем по формуле Бернулли:
Пример. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них 
Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:
D – в n-ом испытании А произошло;
С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
Видеоурок про формулу Бернулли
Для тех, кому нагляднее последовательное видеообъяснение, 15-минутный ролик:
Независимые испытания и формула Бернулли
Сегодня на уроке мы познакомимся с ещё одним распространённым следствием теорем сложения и умножения вероятностей, которое касается независимых испытаний, и рассмотрим многочисленные примеры на использование формулы Бернулли. Данная задача входит в «обязательный комплект» типовой самостоятельной/контрольной работы по теории вероятностей, поэтому ваше ближайшее времяпровождение будет крайне полезным. Кроме того, я расскажу, в чём заблуждается подавляющее большинство участников лотерей и азартных игр. …Нееет, вера или слабая надежда «сорвать куш» тут совершенно ни при чём 😉 Не успев и глазом моргнуть, погружаемся в тему:
Что такое независимые испытания? Практически всё понятно уже из самого названия. Пусть производится несколько испытаний. Если вероятность появления некоего события 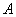
Простейшие примеры:
– монета подбрасывается 10 раз;
– игральная кость подбрасывается 20 раз.
Совершенно ясно, что вероятность выпадения орла либо решки в любом испытании не зависит от результатов других бросков. Аналогичное утверждение, естественно, справедливо и для кубика.
А вот последовательное извлечение карт из колоды не является серией независимых испытаний – как вы помните, это цепочка зависимых событий. Однако если карту каждый раз возвращать обратно, то ситуация станет «такой, какой надо».
Спешу обрадовать – у нас в гостях очередной Терминатор, который абсолютно равнодушен к своим удачам/неудачам, и поэтому его стрельба представляет собой образец стабильности =):
Стрелок совершает 4 выстрела по мишени. Вероятность попадания при каждом выстреле постоянна и равна 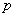
а) стрелок попадёт только один раз;
б) стрелок попадёт 2 раза.
Решение: условие сформулировано в общем виде и вероятность попадания в мишень при каждом выстреле считается известной. Она равна 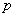
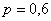
Коль скоро мы знаем 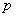
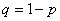
а) Рассмотрим событие «Стрелок попадёт только один раз» и обозначим его вероятность через 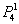
По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
Внимание! Если вам НЕ ПОНЯТНА эта запись, пожалуйста, вернитесь к предыдущему уроку по вышеприведённой ссылке!
Упростим результат с помощью комбинаторной формулы количества сочетаний:
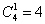
И, поскольку в каждом случае имеет место 1 попадание и 3 промаха, то:
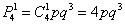
…Как-то так «с лёгкой руки» я начал называть повторные независимые испытания «попытками», что не в каждой задаче может быть корректным… …ну да ладно.
б) Рассмотрим событие «Стрелок попадёт два раза» и обозначим его вероятность через 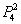
в 1-й и 2-й попытках
или
в 1-й и 3-й попытках
или
в 1-й и 4-й попытках
или
во 2-й и 3-й попытках
или
во 2-й и 4-й попытках
или
в 3-й и 4-й попытках.
Таким образом, по тем же теоремам сложения и умножения вероятностей:
Можно ли так решать задачу? Безусловно, можно. Но что делать, если серия состоит из 5, 6 или бОльшего количества выстрелов? Тут уже будут получаться десятки слагаемых, запись которых отнимет много времени и места. В этой связи рациональнее придерживаться более компактной схемы:
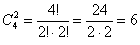
И, поскольку в любом исходе ровно 2 попадания и 2 промаха, то:
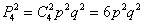
Ответ:
Итак – вероятность того, что будет 1 попадание из 4, равна 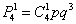
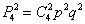
Только что на конкретном примере мы повторили путь Якоба Бернулли, который несколько веков назад вывел формулу, названную позже в его честь:
– Вероятность 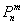
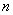
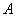
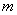
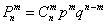
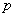
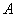
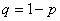
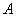
Коэффициент 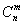
Примечание: формула Бернулли справедлива только для тех независимых испытаний,
в которых вероятность 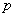
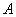
За примером далеко ходить не будем:
Найти вероятность того, что при 10 бросках монеты орёл выпадет 3 раза.
Решение: сначала немного порассуждаем: всего проводится 10 повторных независимых испытаний. Сколькими способами можно выбрать 3 испытания, в которых выпадет орёл?
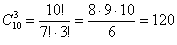
Это что же получается – записывать 120 слагаемых, в каждом из которых 10 множителей? =)
Используем формулу Бернулли: 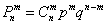
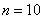
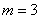
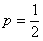
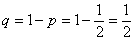
Таким образом:
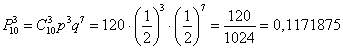
Ответ:
Следует отметить, что повторный характер независимых испытаний не является «жизненно важным» (необходимым) условием для применения формулы Бернулли. Рассмотрим похожую задачу (которая, кстати, эквивалентна Задаче 8 урока о классическом определении вероятности):
Найти вероятность того, что при броске 10 монет орёл выпадет на 3 монетах.
Здесь испытания не повторяются, а скорее, производятся одновременно, но, тем не менее, работает та же самая формула: 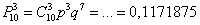
Решение будет отличаться смыслом и некоторыми комментариями, в частности:
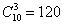
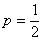
и т.д.
Однако на практике подобные задачи встречаются не столь часто, и, видимо, по этой причине формула Бернулли чуть ли не стереотипно ассоциируется только с повторными испытаниями. Хотя, как только что было показано, повторяемость вовсе не обязательна.
Следующая задача для самостоятельного решения:
Игральную кость бросают 6 раз. Найти вероятность того, что 5 очков:
а) не выпадут (выпадут 0 раз);
б) выпадут 2 раза;
в) выпадут 5 раз.
Результаты округлить до 4 знаков после запятой.
Краткое решение и ответ в конце урока.
Очевидно, что в рассматриваемых примерах некоторые события более вероятны, а некоторые – менее вероятны. Так, например, при 6 бросках кубика даже безо всяких расчётов интуитивно понятно, что вероятности событий пунктов «а» и «бэ» значительно больше вероятности того, что «пятёрка» выпадет 5 раз. А теперь поставим задачу найти
НАИВЕРОЯТНЕЙШЕЕ число появлений события  в
в  независимых испытаниях
независимых испытаниях
Опять же на уровне интуиции в Задаче №3 можно сделать вывод о том, что наивероятнейшее количество появлений «пятёрки» равно единице – ведь всего граней шесть, и при 6 бросках кубика каждая из них должна выпасть в среднем по одному разу. Желающие могут вычислить вероятность 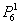
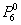
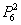
Сформулируем строгий критерий: для отыскания наивероятнейшего числа 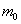
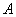
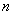
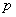
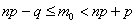
1) если значение 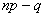
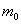
в частности, если 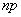
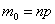
2) если же 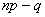
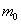
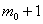
Наивероятнейшее число появлений «пятёрки» при 6 бросках кубика подпадает под частный случай первого пункта:
В целях закрепления материала решим пару задач:
Вероятность того, что при броске мяча баскетболист попадёт в корзину, равна 0,3. Найти наивероятнейшее число попаданий при 8 бросках и соответствующую вероятность.
А это уже если и не Терминатор, то, как минимум, хладнокровный спортсмен =)
Решение: для оценки наивероятнейшего числа попаданий используем двойное неравенство 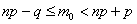
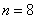
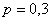
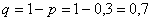
Таким образом, наивероятнейшее количество попаданий при 8 бросках находится в следующих пределах:
Поскольку левая граница – дробное число (пункт №1), то существует единственное наивероятнейшее значение, и, очевидно, что оно равно 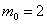
Используя формулу Бернулли 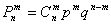
Ответ: 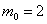
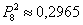
Аналогичное задание для самостоятельного решения:
Монета подбрасывается 9 раз. Найти вероятность наивероятнейшего числа появлений орла
Примерный образец решения и ответ в конце урока.
А сейчас весьма любопытная ситуация: предположим, что во всех 9 испытаниях выпал орёл. Это, кстати, не являются каким-то уж сильно невероятным событием: 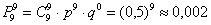
Вопрос: какая сторона монеты вероятнее всего выпадет в 10-м испытании?
Решка? Глубокое заблуждение!
Правильный ответ: вероятности останутся равными! Почему? Причина была сформулирована ещё в самом начале урока: поскольку испытания независимы, то вероятность выпадения орла либо решки в любом испытании не зависит от результатов других испытаний!
Однако игры разума таковы, что у многих людей напрашивается следующий вывод: «раз орёл выпал много раз подряд, то теперь выпадение решки гораздо (!) вероятнее». В теории и на практике этот психологический феномен получил название «Ошибка игрока». Если подбрасывать монету тысячи, десятки тысяч раз, то соотношение орлов/решек будет примерно равным (о чём мы ещё поговорим в статье Статистическое определение вероятности). Но в этом процессе неоднократно встретятся эпизоды, когда монету «заклинит» на какой-то одной грани; и КАК ИМЕННО распределятся эти «необычные» случаи на длинной дистанции – никто не знает.
К слову, о «необычности». Любая случайная последовательность девяти орлов/решек так же вероятна, как и выпадение 9 орлов! Проверить данный факт легче лёгкого: запишем произвольную последовательность исходов, например:
Орёл/Решка/Решка/ Орёл /Решка/ Орёл /Решка/ Орёл /Орёл
По теореме умножения вероятностей независимых событий, вероятность появления этой цепочки: 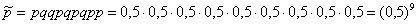
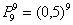
И здесь мы сталкиваемся со второй иллюзией – человек склонен считать «красивые» комбинации чем-то из ряда вон выходящим и чуть ли не фантастическим. Но на самом деле ничего «необычного», например, в комбинации О/О/О/Р/Р/Р/О/О/О – нет, и она может запросто появиться в серии испытаний. Вероятность получить, скажем, пиковый «Ройял-флеш» в покере составляет 1:2598960, однако мало кто задумывается, что с той же вероятностью приходит ЛЮБАЯ, в том числе, совершено «мусорная» комбинация из пяти карт! И с этой точки зрения «сверхъестественная» комбинация 10, В, Д, К, Т пик ничем не примечательна – встречалась «в истории» наряду с другими очень много раз.
Кстати, к теме нашего разговора относятся и типичные ситуации в карточных играх – когда «карта идёт» и наоборот – когда «постоянно сдают один мусор» или «фатально не везёт». Такие «полосы» бывают у каждого игрока, и никакой мистики в этом нет.
На просторах Интернета часто встречается популярный «секрет выигрыша» в рулетку, также известный под названием «Мартингейл». Примерная суть состоит в следующем: «Ставьте на красное. Если выпало чёрное, удваивайте ставку и снова ставьте на красное. Если снова выпало чёрное, то ещё раз удваивайте ставку и снова ставьте на красное и т.д.». Казалось бы – вот оно, золотое дно, ведь красных секторов целых 18 из 37 (18 черных и 1 зеро в европейской рулетке)! И уж «красное» должно выпасть если не на 5-й, то на 10-й раз точно, что позволит отыграть всё ранее поставленное с прибылью!
Ничего подобного! Вероятность выпадения красного сектора в любом испытании постоянна 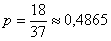
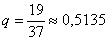
Остаётся вопрос: так почему же этот «удивительный способ» рекламируется в Сети на каждом шагу? Ответ прост: казино распиливает с владельцем сайта-лохотрона проигранные деньги каждого привлечённого Буратино. И что совсем забавляет – «благодетель» просит, чтобы особо везучие лохи отблагодарили его материально (обычно депозит сливается далеко не сразу и поначалу можно даже неплохо подняться). Кто виноват? Конечно же, мошенническая «шарашка», которая специально настроила программное обеспечение на «невероятный» проигрыш. Что делать? Попытать удачи в других заведениях.
«Ошибка игрока» совершается и многими участниками лотерей. На сайте одной лотереи на самом видном месте расположена информация о том, «какие номера давно не выпадали». И вот – целая армия энтузиастов начинает собирать статистику тиражей, подгадывать определённые комбинации и т.д. Чистой воды химера и пустая трата времени – если, например, №8 не выпадал 50 раз подряд, то он с таким же успехом может не выпасть ещё 150 розыгрышей (это не ирония – я в прямом смысле). Однако если провести десятки тысяч тиражей, то количество появлений всех номеров будет примерно равным. Но В КАКОМ ПОРЯДКЕ И КАКИМИ СЕРИЯМИ будет выпадать та же «восьмёрка» на длинной дистанции – никто предсказать не может.
«Русское лото» в этом смысле честнее – оно призывает «поставить на любимые номера», т.е. приобрести билет (онлайн), в котором присутствуют понравившиеся числа.
Но в действительности нет никакой разницы – покупаете ли вы билет наугад, или выбираете билет с определёнными числами, или даже если заполняете бланк самостоятельно. Это если не учитывать потусторонние силы =)
После увлекательного отступления рассмотрим ещё несколько задач, а затем я поделюсь секретом правильной игры в азартные игры и лотереи.
Среди изделий, произведенных на станке-автомате, в среднем бывает 60% изделий первого сорта. Какова вероятность того, что среди 6 наудачу отобранных изделий будет:
а) от 2 до 4 изделий первого сорта;
б) не менее 5 изделий первого сорта;
в) хотя бы одно изделие более низкого сорта.
Вероятность производства первосортного изделия не зависит от качества других выпущенных изделий, поэтому здесь идёт речь о независимых испытаниях. Старайтесь не пренебрегать анализом условия, а то может статься – события-то зависимые или задача вообще о другом.
Решение: вероятность зашифрована под проценты, которые, напоминаю, нужно разделить на сто: 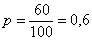
Тогда: 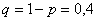
а) Событие «Среди 6 наудачу отобранных изделий будет от 2 до 4 изделий первого сорта» состоит в трёх несовместных исходах:
среди 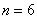
С исходами удобнее разделаться по отдельности. Трижды используем формулу Бернулли 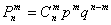
По теореме сложения вероятностей несовместных событий:
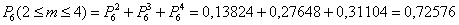
Решение можно было записать и «одной строкой», что мы, впрочем, сделаем в следующем пункте:
б) Событие «Среди 6 наудачу отобранных изделий будет не менее 5 изделий первого сорта» состоит в 2 несовместных исходах: первосортных изделий будет пять или шесть.
По теореме сложения вероятностей несовместных событий: 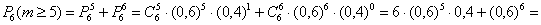
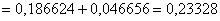
в) Вероятность того, что «Среди 6 наудачу отобранных изделий будет хотя бы одно изделие более низкого сорта» удобно найти через вероятность противоположного события («Все изделия будут первосортными»), которая уже известна:
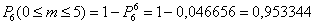
Ответ:
Давайте заодно вспомним такое полезное понятие, как полная группа событий. Что осталось не найденным? Остались не найденными вероятности двух событий.
Не знаю кому как, а мне порядком поднадоел микрокалькулятор, и я предлагаю воспользоваться расчётным макетом по теории вероятностей – это подарок для самых прилежных студентов, которые не уходят курить во время моих занятий =)
Вводим исходные данные и получаем:
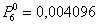
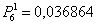
Проверка: 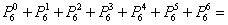
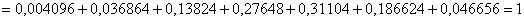
что и требовалось проверить.
Небольшое задание для самостоятельного решения:
Производится 8 выстрелов по цели, в каждом из которых вероятность попадания равна 0,1. Найти вероятность того, что цель будет поражена хотя бы два раза.
Краткое решение и ответ в конце урока.
Следует отметить, что задачи на формулу Бернулли «хорошо узнаются» и обычно не вызывают затруднений. С дополнительными, в том числе весьма интересными примерами по теме можно ознакомиться в этой pdf-ке с готовыми решениями. И одну из таких задач я разберу в заключение урока:
Для нормальной работы вычислительного центра необходима безотказная работа в течение дня, как минимум, 5 компьютеров. Сколько компьютеров нужно установить, чтобы с вероятностью, не меньшей 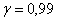
Решение: из условия легко найти, что вероятность безотказной работы любого компьютера в течение дня составляет 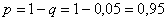
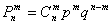
Поскольку для нормальной работы центра необходима безотказная работа, как минимум, 5 компьютеров, то может быть пяти и хватит?
1) Если в вычислительном центре установить 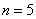
Но по условию нормальную работу центра нужно обеспечить с вероятностью, не меньшей, чем 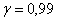
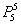
2) Предположим, что в вычислительном центре установлено 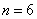
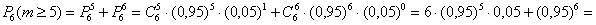
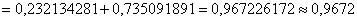
Данное значение нас тоже не устроит, так как оно меньше требуемой надёжности работы вычислительного центра:
Таким образом, шести компьютеров тоже не достаточно. Добавляем ещё один:
3) Пусть в вычислительном центре 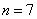
Есть! Требуемый уровень надёжности достигнут.
Можно, конечно, поставить и бОльшее количество компьютеров, но зачем переплачивать? =)
Ответ: чтобы обеспечить нормальную работу вычислительного центра в течение дня с вероятностью, не меньшей 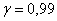
Формула Бернулли очень удобна, но с другой стороны, обладает и рядом недостатков. Так, например, при достаточно больших значениях «эн» и «эм» её применение затруднено ввиду огромных значений факториалов. В этом случае используют теоремы Лапласа, которые мы рассмотрим на следующем уроке. Другая распространённая на практике ситуация – когда вероятность 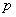
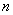
И, наконец, обещанный секрет:
…Так всё-таки – как правильно играть в азартные игры и лотереи?
Наверное, многие ожидали услышать от меня что-нибудь вроде: «Лучше вообще не играть», «Открыть собственное казино», «Организовать лотерею» и т.п.
Ну почему же не играть? Игра – это одно из развлечений, а за развлечения, как известно, нужно… совершенно верно! Поэтому средства, на которые вы играете, следует считать платой за развлечение, но ни в коем случае трагической потерей.
Тем не менее, каждый участник азартной игры хочет выиграть. И выиграть хорошую сумму. Какой тактики (о стратегии речи не идет вообще) выгоднее всего придерживаться в игре с заведомо проигрышным математическим ожиданием, например, в рулетке? Лучше всего сразу поставить все фишки, как вариант, на «красное» либо «чёрное». С вероятностью 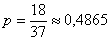
Не имеет смысла играть по какой-то «системе» (хотя бы потому, что это глупо) и тратить на это часы/дни/недели – в той же рулетке заведение имеет минимальное преимущество, и проигрываться можно ооооочень долго. Если в оффлайновом казино это ещё как-то можно понять (общение, выпивка, девочки и т.д.), то онлайн игра оставит вас с красными глазами и чувством глубокой досады.
Что касается лотерей, то билет лучше покупать опять же ради развлечения и… наобум. Или «по наитию». Правда, лично я почему-то никогда не слышал об экстрасенсах и предсказателях, которые выигрывают в лотереи =) Не иначе, как шифруются.
Естественно, перечисленные советы не относятся к хроническим лудоманам и им как раз таки «Лучше вообще не играть». Ну а тем посетителям, которые мечтают разбогатеть на гэмблинге, настоятельно рекомендую прочитать либо ещё раз перечитать вводную статью по теории вероятностей.
Задача 3: Решение: используем формулу Бернулли: 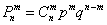
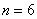
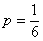
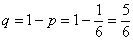
а) 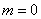
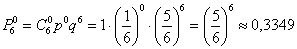
б) 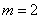
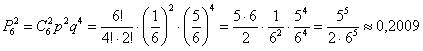
в) 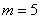
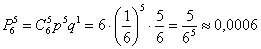
Ответ:
Задача 5: Решение: в данной задаче речь идёт о независимых испытаниях, при этом:
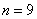
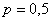
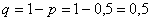
Найдём наивероятнейшее количество 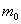
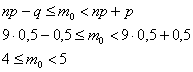
Так как 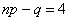
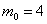
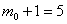
Используя формулу Бернулли, вычислим соответствующие вероятности: 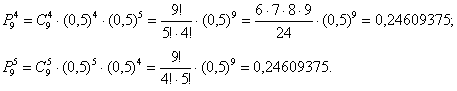
Ответ: 4 и 5;
Задача 7: Решение: используем формулу Бернулли: 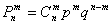
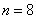
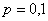
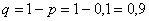
По теореме сложения вероятностей несовместных событий:
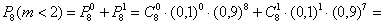
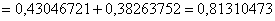
Найдём вероятность противоположного события:
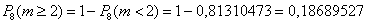
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5