Что такое самопересечение в геометрии

Ломаная линия

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

Замкнутая и незамкнутая ломаная

Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.

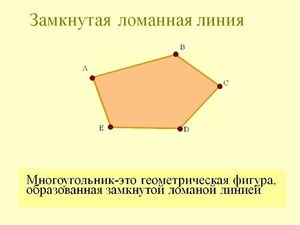
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Источник

Самопересечения точка

Смотреть что такое «Самопересечения точка» в других словарях:

САМОПЕРЕСЕЧЕНИЯ ТОЧКА — одна из особых точек кривой или поверхности. См., напр., Двойная точка … Математическая энциклопедия

Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… … Большая советская энциклопедия

Точка — I Точка (математическая) одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых… … Большая советская энциклопедия

Узловая точка — самопересечения точка, Особая точка кривой … Большая советская энциклопедия

УЗЛОВАЯ ТОЧКА — точка самопересечения кривой. При параметрич. задании кривой У. т. соответствует двум или более значениям параметра. Например, у кривой а sinЗj У. т. начало координат … Математическая энциклопедия

ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия

Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия

Особая точка — указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой… … Википедия

Особая точка функции — Особая точка указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например,… … Википедия

ДВОЙНАЯ ТОЧКА — один из видов особых точек кривой F(x, y) = 0, в к рой первые частные производные равны нулю и по крайней мере одна из вторых частных производных функции F(х, у)не равна нулю. При исследовании строения кривой вблизи Д. т. рассматривают знак… … Математическая энциклопедия

Источник

Как выглядит замкнутая ломаная линия

Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.

Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:

Типы ломаных линий

Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.

Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.

Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.

Всего существует 4 типа подобных линий по своей структуре:

Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.

Особенности замкнутых линий

Рассмотрим подробнее составляющие части этой геометрической фигуры.

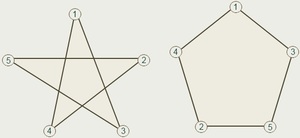
Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.

Многоугольник как разновидность замкнутой ломаной

Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.

Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.

Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.

Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.

У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.

Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.

Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.

Источник

Замкнутые самопересекающиеся ломаные

Александр Блинков, Александр Грибалко
«Квантик» №11, 2019

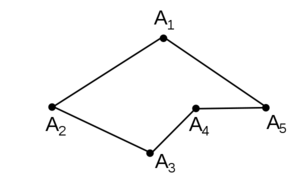
В этой статье пойдёт речь о ломаных линиях на плоскости. Для того чтобы изобразить ломаную, достаточно выбрать несколько точек (не меньше трёх), занумеровать их в каком-нибудь порядке, после чего последовательно соединить отрезками точки с соседними номерами. Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).

Если хотя бы два звена ломаной пересекаются (в своих внутренних точках), её называют самопересекающейся (на рисунке 2 — четырёхзвенная самопересекающаяся ломаная).

И наконец, если первая и последняя вершины ломаной совпадают, её называют замкнутой. В такой ломаной количество вершин совпадает с количеством звеньев (на рисунке 3 изображена пятизвенная замкнутая ломаная).

Нас будут интересовать замкнутые самопересекающиеся ломаные.

Начнём с задачи, предложенной А. Пешниным (её частные случаи были использованы на XXV турнире математических боёв имени А. П. Савина).

Задача 1

Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно два раза?

Очевидно, что трёхзвенная замкнутая ломаная не может быть самопересекающейся. Замкнутая ломаная с четырьмя вершинами также не удовлетворяет условию задачи, так как соседние звенья пересечься не могут, а для каждого звена есть только одно не соседнее. Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.

Этот пример подсказывает, что аналогичным образом можно построить любую ломаную, удовлетворяющую условию, с нечётным количеством звеньев, большим трёх. Достаточно поставить на окружности требуемое количество вершин и последовательно соединить их через одну. Например, на рисунке 4, б — искомая ломаная с девятью звеньями.

Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.

Искомой шестизвенной ломаной не существует, но доказывать это мы умеем только перебором всех случаев, который не очень интересен.

Для восьми звеньев существует красивый пример (рис. 5, а). Аналогично можно построить ломаную, удовлетворяющую условию, с любым чётным количеством звеньев, большим восьми. Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.

Есть и более простой способ. Воспользуемся тем, что любое чётное число, большее восьми, можно представить в виде суммы двух нечётных слагаемых, каждое из которых не меньше пяти.

Покажем, например, как построить двенадцатизвенную ломаную, удовлетворяющую условию. Изобразим две окружности, которые касаются друг друга внешним образом в некоторой точке. В одной из окружностей построим уже указанным способом пятизвенную ломаную, а в другой — семизвенную, причём точка касания должна быть их общей вершиной. А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).

Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.

Возникает вопрос: почему мы начали с двух точек пересечения звеньев, а не с одной, что, казалось бы, более естественно?

Дело в том, что такой порядок более логичен, так как решение следующей задачи будет во многом опираться на решение рассмотренной.

Задача 2

Сколько вершин может быть у замкнутой ломаной, которая каждое своё звено пересекает ровно один раз?

Сразу заметим, что в этом случае звенья ломаной должны разбиваться на непересекающиеся пары, поэтому у искомых ломаных — чётное количество звеньев. Легко проверить, что замкнутая ломаная из четырёх звеньев условию не удовлетворяет.

Пример искомой ломаной из шести звеньев можно построить, исходя из следующих соображений: помимо того, что не могут пересекаться соседние звенья, не могут пересекаться и звенья, стоящие через одно. Действительно, в этом случае образуется треугольник (рис. 7, а), в который можно будет только «войти», если пересечь среднее звено, но нельзя будет «выйти». Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).

Пример искомой ломаной из восьми звеньев читателю предлагается построить самостоятельно (см. задачи в конце статьи). А вот пример десятизвенной ломаной можно получить, обратившись к задаче 1. Действительно, рассмотрим пример замкнутой пятизвенной ломаной, которая каждое своё звено пересекает два раза (рис. 4). «Сломаем» каждое звено между двумя точками пересечения и получим искомый пример (рис. 8). Аналогично, рассмотрев семизвенную ломаную из задачи 1, можно получить решение для ломаной с четырнадцатью звеньями; пример восьмизвенной ломаной из задачи 1 помогает получить решение для ломаной из шестнадцати звеньев, и т. д.

Этот приём не годится только для построения двенадцатизвенной ломаной, так как нет шестизвенной ломаной, которая каждое своё звено пересекает два раза. Но в этом случае можно использовать другую идею решения задачи 1: «раздвоение». Построим две ломаные из рис. 7, б с общей вершиной и «раздвоим» её (рис. 9, результат раздвоения — вершины с номерами 6 и 12). Понятно, что идея «раздвоения» вершин более универсальна. В том числе и потому, что позволяет комбинировать ломаные с разным количеством звеньев.

Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.

Упражнения и задачи для самостоятельного решения

1. Может ли прямая, не содержащая вершин замкнутой девятизвенной ломаной, пересечь каждое её звено?

2. (В. Произволов) Замкнутая ломаная такова, что каждые два её не соседних звена пересекаются. Докажите, что у этой ломаной нечётное количество звеньев.

3. Существует ли пятнадцатизвенная ломаная, пересекающая каждое своё звено ровно три раза?

4. Постройте восьмизвенную замкнутую ломаную, которая каждое своё звено пересекает один раз.

5. (Д. Калинин, вариация фольклора) Маша нарисовала замкнутую семизвенную ломаную. Для каждого звена она записала, со сколькими звеньями оно пересекается во внутренних точках. Могла ли она записать в каком-то порядке числа 1, 2, 3, 4, 3, 2, 1?

6. Какое наибольшее количество точек самопересечения может иметь замкнутая семизвенная ломаная?

7. (Н. Васильев) Рассматриваются всевозможные шестизвенные замкнутые ломаные, все вершины которых лежат на окружности.

Источник

САМОПЕРЕСЕЧЕНИЯ ТОЧКА

одна из особых точек кривой или поверхности. См., напр., Двойная точка.

Смотреть что такое «САМОПЕРЕСЕЧЕНИЯ ТОЧКА» в других словарях:

Самопересечения точка — узловая, кратная точка, одна из особых точек (См. Особая точка) кривой … Большая советская энциклопедия

Точка (матем.) — Точка (математическая), одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых состоят… … Большая советская энциклопедия

Точка — I Точка (математическая) одно из основных понятий геометрии. При систематическом изложении геометрии Т. обычно принимается за одно из исходных понятий. В современной математике Т. называются элементы весьма различной природы, из которых… … Большая советская энциклопедия

Узловая точка — самопересечения точка, Особая точка кривой … Большая советская энциклопедия

УЗЛОВАЯ ТОЧКА — точка самопересечения кривой. При параметрич. задании кривой У. т. соответствует двум или более значениям параметра. Например, у кривой а sinЗj У. т. начало координат … Математическая энциклопедия

ОСОБАЯ ТОЧКА — 1) О. т. аналитической функции f(z) препятствие для аналитического продолжения элемента функции f(z) комплексного переменного zвдоль какого либо пути на плоскости этого переменного. Пусть аналитическая функция f(z) определена некоторым… … Математическая энциклопедия

Особая точка — в математике. 1) Особая точка кривой, заданной уравнением F (x, у) = 0, точка М0(х0, y0), в которой обе частные производные функции F (x, у) обращаются в нуль: Если при этом не все вторые частные производные… … Большая советская энциклопедия

Особая точка — указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например, точка в которой… … Википедия

Особая точка функции — Особая точка указывает сюда. См. также особая точка (дифференциальные уравнения). Особенность или сингулярность в математике это точка, в которой математический объект (обычно функция) не определён или имеет нерегулярное поведение (например,… … Википедия

ДВОЙНАЯ ТОЧКА — один из видов особых точек кривой F(x, y) = 0, в к рой первые частные производные равны нулю и по крайней мере одна из вторых частных производных функции F(х, у)не равна нулю. При исследовании строения кривой вблизи Д. т. рассматривают знак… … Математическая энциклопедия

Источник