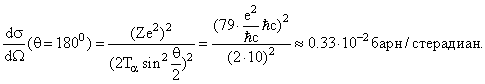Что такое сечение рассеяния
Что такое сечение рассеяния
Основным экспериментальным методом изучения взаимодействий элементарных частиц и ядер со времен Резерфорда является их рассеяние друг на друге 1 . Информация о свойствах частиц и их взаимодействий извлекается, в первую очередь, из данных о вероятностях тех или других процессов, происходящих при столкновении этих частиц. Эта вероятность, в свою очередь, определяется величиной т. н. «поперечного сечения» данной реакции, связанного непосредственно с квадратом модуля амплитуды ее вероятности и «размером» той области в т. н. «фазовом пространстве», в которой могут оказаться конечные продукты реакции. Границы этой области однозначно определяются законами сохранения энергии-импульса, т. е. кинематикой рассматриваемой реакции. Некоторые зоны в разрешенной области могут оказаться недоступными, образуя «каверны» [2] (или наоборот, предпочтительными, т. е. «зонами концентрации», или «аттракторами») для конечных продуктов из-за запретов или других требований, накладываемых на конечные состояния законами сохранения квантовых чисел (спина, четности, изоспина) или следствиями статистики Ферми или Бозе-Эйнштейна и т. д. Все это тоже является предметом рассмотрения кинематики.
Перед обсуждением этих и подобных им вопросов, представляется естественным вначале напомнить, что такое поперечное сечение реакции и как эта величина измеряется экспериментально. Для этого взят пример полных сечений рассеяния (энергозависимость которых была показана в Части I) и уделено внимание ряду деталей, нечасто упоминаемых в учебниках или специальных обзорах, но важных для знакомства с методикой измерений.
8.1 Сечения реакций
8.1.1 Определение сечения рассеяния
Напомним определение поперечного сечения рассеяния. Пусть сталкиваются два пучка частиц с плотностями na, nb и скоростями va, vb (не обязательно коллинеарными). В системе покоя частиц b скорость частиц a есть 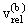
справедлива и в релятивистском, и в нерелятивистском случае. В этой формуле плотности помечены индексом (0) чтобы подчеркнуть, что они берутся в системе покоя соответствующих частиц (полезно помнить, что плотность частиц есть их число в единице объема). Существенное изменение в формуле (8.2) состоит в том, что величина uab есть пространственная компонента относительной 4-скорости частиц a и b.
В литературе существуют другие, более традиционные, формы записи, в которых единство нерелятивистской и релятивистской записи выражения для числа столкновений увидеть сложнее. Релятивистское обобщение формулы (8.1) обычно делается с помощью введения понятия т. н. Мёллеровского инвариантного потока, который, если привлечь понятие относительной 4-скорости, может быть записан как
(Здесь 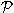
Мёллеровский инвариантный поток можно представить в иной форме, используя только инвариант sab − квадрат полной энергии в системе центра масс частиц a и b и определение (3.29) треугольной функции:
где p* есть импульс частицы a или b в их системе центра масс; для получения последнего равенства использовано соотношение (3.29). Формула (8.4) пригодится в дальнейшем, а последнее равенство в ней особенно удобно при рассмотрении экспериментов на коллайдерах, когда лабораторный импульс частиц каждого из сталкивающихся встречных пучков (при угле встречи 0°) есть просто p*.
8.1.2 Как измерять поперечные сечения?
Ответ на этот вопрос прост: в формулах (8.1) или (8.2) спрятано не только определение сечения рассеяния, но и идея метода его экспериментального измерения. Действительно, пусть мишень b в лабораторной системе отсчета покоится. Тогда nb (0) dV = ρ·l·dS·NA/A есть число частиц мишени в трубке длиной l с поперечным сечением dS, а na (0) cdt | uab | − число частиц пучка, упавших на единицу площади мишени за время dt. Обычно поперечное сечение пучка меньше мишени (т. к. мишень, как правило, полностью перехватывает пучок); поэтому множитель dS можно перебросить в часть, относящуюся к пучку. Тогда за время T облучения мишени пучком с поперечным размером S число столкновений, зарегистрированных детектором, будет равно
где Ncycl − число циклов ускорителя за время T, δ − «duty factor»(скважность), τ − длительность импульса излучения, I − число частиц в импульсе излучения. Эту формулу можно переписать в ином виде, введя понятие светимости L
В формуле (8.6) светимость записана для случая т. н. «экспериментов с неподвижной мишенью» (мишень покоится в лабораторной системе). Однако это понятие чаще используется для экспериментов на коллайдерах, когда встречаются два пучка частиц и между ними происходят столкновения. Вид формулы для светимости в этом случае иной.
Дальше все зависит от того, как детектор регистрирует сам факт столкновения и какого типа столкновения он «умеет» распознавать. Зная светимость и подсчитав число зарегистрированных столкновений нужного типа, легко найти сечение соответствующих реакций.
Одна из важных экспериментально наблюдаемых характеристик реакций рассеяния − полное сечение рассеяния, которое определяет вероятность того, что произойдет какое бы то ни было взаимодействие снаряда и мишени: упругое рассеяние, неупругое взаимодействие с возбуждением любой из взаимодействующих частиц, неупругое рассеяние (с рождением любого числа частиц, допустимого законами сохранения и возможного при данной энергии снаряда).
8.2 Обобщенная схема измерений
Чтобы понять, как можно измерить полное сечение рассеяния, найдем сначала ответ на следующий вопрос. Пусть параллельный монохроматический пучок падает нормально на плоскопараллельную пластинку толщины x по направлению пучка. Какова вероятность P0(x) того, что частица пучка пройдет через вещество пластинки не испытав ни одного столкновения со структурными единицами (например, ядрами атомов) ее вещества?
Очевидно, что число рассеивающих ядер на пути пучка, взятое на единицу площади пластинки (число рассеивающих центров), есть
где ρ − плотность вещества пластинки, 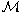
Увеличим толщину пластинки на бесконечно малую величину dx. То, что и после этого какая-то из частиц пучка по-прежнему не испытала ни одного столкновения, означает, что случилось событие, состоящее из двух следующих последовательных частных событий: (1) не было ни одного столкновения при прохождении слоя x, (2) не было ни одного столкновения при прохождении добавочного слоя dx. Вероятность первого частного события есть P0(x). Какова же вероятность второго частного события? Очевидно, что раз слой бесконечно тонок, то могут быть только 2 взаимоисключающих исхода: либо ничего не случится (вероятность чего и надо найти), либо случится одно столкновение, вероятность чего есть Ncenters(dx)·σtot в соответствии с определением сечения рассеяния. Сумма вероятностей этих событий есть 1, а значит, P0(dx) = 1 − Ncenters(dx)·σtot. То есть,
Но это означает, что
Общее решение этого уравнения хорошо известно; вспоминая очевидное граничное условие
P0(0) = 1 (т. е. при нулевой толщине пластинки с вероятностью 1 рассеяния не будет), приходим к знакомому из оптики (и других разделов классической физики) закону:
где ncenters − число рассеивающих центров на единицу толщины пластинки. Соответственно,
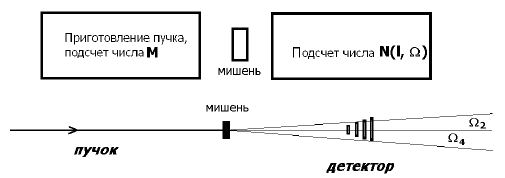
Формула (8.11) лежит в основе одного из широко распространенных способов экспериментального измерения полных сечений рассеяния. В этом способе сравниваются интенсивности падающего пучка и пучка, прошедшего через пластинку-мишень без взаимодействия. Такой метод называется трансмиссионным. Реализовать его в реальном мире не так уж и просто, особенно если речь идет о точных измерениях: пучки никогда не бывают идеальными, сосчитать число упавших на мишень частиц не всегда легко, и того сложнее определить, прошла ли частица через мишень без взаимодействия или же оно имело место. Обобщенная схема измерений полных сечений рассеяния методом измерения коэффициента трансмиссии 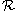
Рис. 8.1. Обобщенная схема измерений полных сечений трансмиссионным методом (вверху) и типичная схема реального эксперимента в условиях «хорошей геометрии» (внизу).
8.3 Трансмиссионный метод: детали
В этом методе основная экспериментальная проблема − нахождение интенсивности нерассеянного пучка. Информация о величине полного сечения рассеяния скрыта в коэффициенте трансмиссии 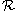
где N(x) = I(x)·Tmeasur, M = I0·Tmeasur, Tmeasur − время измерения. Главные трудности, особенно существенные при стремлении достичь малых (проценты или доли процентов от измеряемой величины) систематических погрешностей, связаны с тем, что:
Итак, рассмотрим упрощенную схему измерений, показанную на рис. 8.1. Будем считать мишень «тонкой», т. е. вероятностью ядерного рассеяния кратности выше 1 можно пренебречь по сравнению с другими источниками погрешностей. Количественно, это означает, что показатель экспоненты в формуле (8.12) мал (см. также задачи 58-54 в Части X). Будем предполагать, что пучок аксиально симметричен, его линейные размеры в поперечном сечении малы и угловая расходимость также невелика (то есть, поперечные размеры пучка в районе мишени и на выходе из экспериментальной установки почти не различаются). Наконец, примем на время, что частица считается «не рассеянной», если она зарегистрирована детектором i. перекрывающим некоторый телесный угол Ωi.
В этих предположениях, (см. также задачу 58 Части X), число частиц, зарегистрированных детектором, перекрывающим телесный угол Ω после мишени, в отсутствии многократного кулоновского рассеяния можно записать как
Если же телесный угол Ω в формуле (8.13) выбран столь малым, что даже многократное кулоновское (мольеровское) рассеяние может вывести из него проходящую через мишень частицу, то эта формула примет иной вид:
Здесь под ƒ(θ) понимается плотность вероятности того, что частица. не испытавшая никакого ядерного рассеяния, окажется зарегистрированной при угле θ в интервале телесных углов (Ω, Ω+dΩ); далее будем называть ее «аппаратурной функцией». Она может включать в себя эффекты мольеровского рассеяния 2 , аппаратурное угловое разрешение, эффекты конечных линейных и угловых параметров пучка. Под обозначениями θ« и θ‘ понимается, что последовательное действие мольеровского рассеяния на угол θ« и ядерного рассеяния на угол θ‘ − θ« оставит частицу в телесном угле с раствором θ. Конечно, здесь всюду пока подразумевается, что поперечный размер пучка бесконечно мал и его расходимость также бесконечно мала. Можно модифицировать эту формулу так, чтобы включить и учет размеров реального пучка, но для понимания основных моментов реализации трансмиссионного метода эти детали несущественны (однако, при выполнении конкретного эксперимента о них нельзя забывать).
Формула (8.14) достаточно реалистична несмотря на то, что в ней не учтено присутствие фонового вещества. Она позволяет провести обсуждение вопросов о выборе величины захватываемых счетчиками угловых интервалов и проблемы экстраполяции.
Первое важное для практики следствие формулы (8.14): метод оправдан, если дифференциальное сечение зависит от угла много медленнее, чем аппаратурная функция ƒ(θ), то есть, существует область углов θ > θ0, где dσ/dΩ еще достаточно велико и меняется с изменением угла захвата (Ω на рис. 8.1), но первый интеграл в формуле (8.14) уже равен 1. В противном случае, чтобы измерить полное сечение рассеяния, необходимо знать также и поведение дифференциального сечения.
8.4 Характерные области углов рассеяния
Проведенное обсуждение уже позволяет выделить первую характерную область углов рассеяния, совершенно непригодную для нахождения полного сечения ядерного рассеяния: это область очень малых углов, где отклонение частицы после прохождения слоя вещества от ее первоначального направления обусловлено рассеянием на электронах многих атомов этого вещества: т. н. многократным кулоновским рассеянием. Характерный пространственный угол многократного рассеяния, как известно, есть
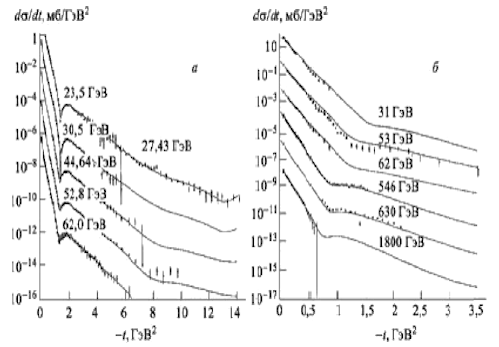
Рис. 8.2. Дифракционное упругое рассеяние протонов (слева) и антипротонов (справа), [79].
Итак, планируя трансмиссионные измерения полных сечений следует выбирать интервал углов вне области кулон-ядерной интерференции с одной стороны, но оставаться в пределах т. н. «дифракционного конуса» с другой (рис. 8.2-8.4).
Область дифракционного конуса отвечает углам рассеяния (или передачам | t |) от самых малых (начиная с тех, где кулоновские эффекты уже несущественны) до области первого дифракционного минимума в дифференциальных сечениях.
Теперь, понимая, что такое поперечное сечение рассеяния и как оно измеряется, можно перейти к рассмотрению его связи с матричным элементом той или иной реакции.
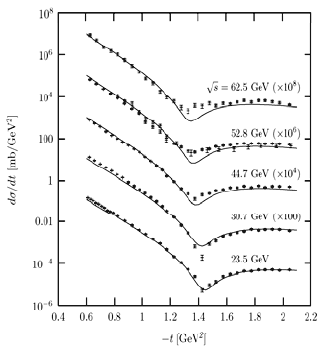
Рис. 8.3. Дифракционное упругое рассеяние протонов еще раз (из работы [80]).
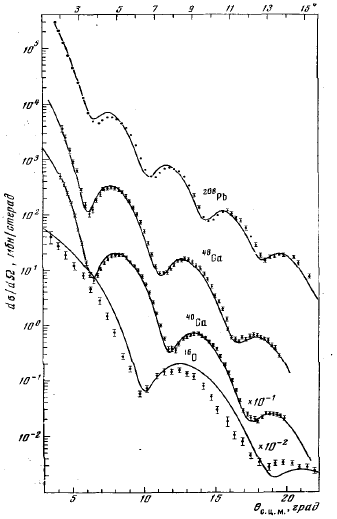 | 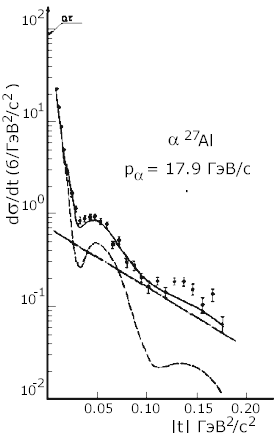 |
Рис. 8.4. Слева: дифференциальные сечения упругого дифракционного рассеяния протонов с
Тkin
1 ГэВ на ядрах от кислорода до свинца, данные ПИЯФ [81]. Справа: дифференциальные сечения упругого дифракционного рассеяния релятивистских ядер гелия-4 на ядрах алюминия; данные ОИЯИ [82].
(1) В классической физике этот метод широко использовался во многих дисциплинах задолго до появления атомной и ядерной физики.
(2) То есть, многократного кулоновского рассеяния, теория которого была дана Мольер, см. университетские курсы о прохождении заряженных частиц через вещество, а также обзоры [62].
Что такое сечение рассеяния
Если на рассеивающий элемент падает звуковая волна с интенсивностью 



Можно ввести также понятие дифференциального сечения рассеяния 



Частным примером дифференциального сечения рассеяния является сечение обратного рассеяния
Сечение поглощения определяется как отношение полной мощности, теряемой первичной волной и преобразующейся в тепло в данной локальной области, к плотности потока энергии (интенсивности) в первичной волне
Сечение затухания представляет собой относительную величину полной мощности, теряемой первичной волной за счет рассеяния и поглощения:
Подобные определения различных сечений применимы к произвольному рассеивающему препятствию в однородной плоской волне,
причем в равной мере их можно использовать как в случае одиночного препятствия, так и при наличии совокупности рассеивателей. В тех средах, где рассеиватели распределены случайным образом и рассматриваемый объем содержит достаточно большое их число, рассеиваемая мощность будет пропорциональна этому объему, и рассеяние называется некогерентным [20]. В этих случаях эффективность рассеяния на совокупности препятствий можно охарактеризовать с помощью сечения рассеяния на единицу объема. Эта величина называется коэффициентом рассеяния 





Пусть на слой некогерентно рассеивающего материала толщиной 


Ослабление интенсивности волны есть 
Здесь предполагается, что энергия, теряемая первичной волной, не возвращается в нее в результате многократного рассеяния.
Сечение рассеяния можно рассчитать, зная звуковое давление в рассеянной волне.
При экспериментальном исследовании рассеяния наиболее удобно проводить измерения звукового давления в дальнем поле рассеивающего препятствия, где рассеянная волна становится сферической (см. уравнение (6.12)):
Интенсивность этой волны есть
откуда поток энергии, теряемой объемом V за счет рассеяния, можно представить в виде
где интегрирование проводится по поверхности 
Коэффициент рассеяния определяется последним выражением, нормированным по отношению к интенсивности падающей волны 
В приближении Борна (см. разд. 6.2.1) полное сечение рассеяния определяется выражением
До сих пор мы определяли все сечения рассеяния для конкретной ориентации рассеивающего препятствия, задаваемой углами 
Для тканей, обладающих аксиальной симметрией, таких как мышцы, целесообразно определять соответствующие сечения рассеяния отдельно для случая, когда волновой вектор первичной волны параллелен мышечным волокнам, и отдельно для тех ситуаций, когда волновой вектор перпендикулярен волокнам.
Кроме того, можно ввести еще несколько усредненных сечений, которые поддаются экспериментальному измерению. Они будут рассмотрены в разд. 6.4.1.
Что такое сечение рассеяния
В физике микромира характеристиками вероятности процессов взаимодействия частиц и ядер являются дифференциальное и полное эффективные сечения реакций.
Рассмотрим поток частиц А, падающих на мишень и вступающих во взаимодействие с частицами мишени В. Результатом реакции может быть как появление частиц А и В с другими кинематическими характеристиками, так и возникновение новых частиц.
Дифференциальное эффективное сечение реакции в системе покоя мишени определяется как
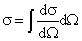
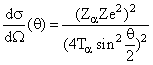
Здесь для упрощения процедуры расчета использована константа электромагнитного взаимодействия и константа конверсии
Расчет аналогичен расчету предыдущей задачи.
Следует отметить, что формула Резерфорда в виде (3.3) справедлива лишь при энергиях 
Диаграммы Фейнмана
В системе единиц 







(соотношение неопределенности Гейзенберга для энергии и времени)
Для виртуальных частиц
Следует подчеркнуть, что в целом для всего процесса законы сохранения выполняются точно, в частности, полная энергия частиц до взаимодействия равна полной энергии частиц после взаимодействия.
На рис. 3.1 изображена диаграмма Фейнмана для рассеяния фотона на электроне. (Вектор времени направлен слева направо). Перемена направлений на фермионной линии дает диаграмму Фейнмана для рассеяния фотона на позитроне. Диаграммы Фейнмана обладают замечательными свойствами: если на рис.1 направить вектор времени снизу вверх
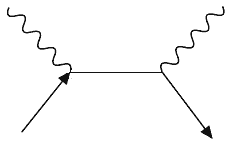
Рис.3.1
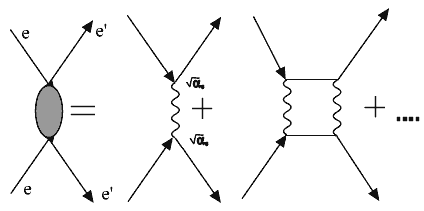
Рис.3.2
Поскольку взаимодействие электромагнитное, каждой вершине соответствует константа электромагнитного взаимодействия
(

Первая из диаграмм Фейнмана, дающая вклад в процесс рассеяния электрона на электроне, имеет две вершины, ее вклад в амплитуду вероятности процесса (матричный элемент процесса M) пропорционален произведению квадрату константы (3.4): M
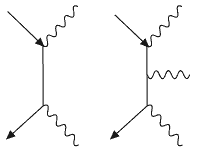
Рис.3.3
Для первого процесса с двумя вершинами вероятностьW1
(d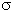
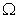
| Задача 3.5. Обосновать справедливость применения формулы Мотта с F = 1 в задаче 3.4. |
Введение формфактора как в формулу Резерфорда, так и в формулу Мотта необходимо в тех случаях, когда длина волны рассеиваемой на ядре частицы меньше, чем диаметр ядра. Для ядра Са-40 диаметр равен приблизительно
Длина волны электрона с кинетической энергией 10 МэВ
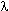

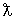

Таким образом, применение формулы Мотта для рассеяния электрона на точечном заряде оправдано для электронов с кинетической энергией 10 МэВ.