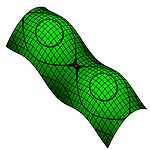
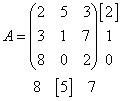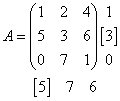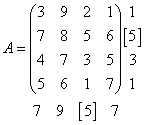Что такое седловая точка

06. Принцип максимина в антагонистических играх. Седловая точка

Как отмечалось, важнейшим вопросом в теории игр (в том числе и матричных) является вопрос о выборе оптимальных стратегий для каждого из игроков.

Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему максимальный выигрыш. Если игра повторяется неоднократно, то оптимальная стратегия должна обеспечивать максимальный средний выигрыш.

При выборе этой стратегии основой рассуждений является предположение, что Противник является, по меньшей мере, так же разумен, как и мы сами, и делает все, чтобы добиться такой же цели.

При этом для выбора оптимальной стратегии используют Принцип максимина: Выбирай ту стратегию, чтобы при наихудшем для нас поведении противника получить максимальный выигрыш. Другими словами, принцип максимина предполагает выбор той стратегии, при которой наш минимальный выигрыш для различных стратегий максимален. Отсюда и название «принцип максимина».

Для пояснения принципа максимина рассмотрим пример 1 матричной игры G (4х5) с платежной матрицей, приведенной на рис. 2.2.

Какой стратегией игроку А воспользоваться? Есть соблазнительный выигрыш 12, при применении стратегии А3. Но при этом противник может выбрать стратегию В3, и игрок А получит выигрыш, равный всего трем.

Для определения оптимальной стратегии в соответствии с принципом максимина, запишем в правом добавочном столбце платежной матрицы минимальное значение AI в каждой строке (минимум строки). Из всех значений AI (правый столбец) выделим наибольшее. Ему соответствует стратегия А4. Выбрав эту стратегию, мы во всяком случае можем быть уверены, что при любом поведении противника выигрыш будет не менее пяти.

Теперь станем на точку зрения игрока В и порассуждаем за него. Выбирая стратегию, он хотел бы отдать поменьше, но должен рассчитывать на наихудшее для него поведение игрока А.

Припишем к платежной матрице (рис.2.2) нижнюю строку и в ней запишем наихудшее для игрока В возможные результаты (максимумы столбцов BJ.

До тех пор, пока обе стороны в нашем примере будут придерживаться своих максиминных стратегий, выигрыш игрока А и проигрыш игрока В будет равен А43=5.

Легко показать, что нижняя цена игры никогда не превосходит верхней цены игры.

Лемма 1. Пусть задана матрица выигрышей

А = êêaijêêи определены b= и a= .

Тогда .

Доказательство. По определению максимума и минимума для любых фиксированных значений I и J имеем

(2.1)

Поскольку левая часть неравенства (2.1) не зависит от I, то можем записать

(2.2)

Так как правая часть неравенства (2.1) не зависит от J, то

(2.3)

Объединяя неравенства (2.2) и (2.3), получаем неравенство (2.1), что и требовалось доказать. Итак, всегда B³A.

Случай B=A, соответствует наличию у платежной матрицы так называемой Седловой точки.

Определение. Точка (I*, J*) называется седловой точкой платежной матрицы ||AIj||, если для всех остальных i и j этой матрицы выполняется условие

Т. е. Аij является одновременно минимумом своей строки и максимумом своего столбца.

Приведем без доказательства следующую теорему.

Теорема 1. Для того чтобы

(2.4)

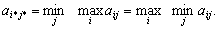
Говорят, что матричная игра имеет седловую точку, если соответствующая ей матрица выигрышей (платежная матрица) имеет седловую точку.

Пример 2. Найти решение игры G (3х3), платежная матрица которой имеет следующий вид:

Источник

Седловая точка в матричных играх

Матричные игры

Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.

Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.

2 Платёжная матрица, чистые стратегии, цена игры

В матричной игре её правила определяет платёжная матрица.

В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.

Составим платёжную матрицу:

.

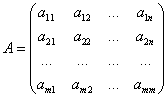
Так как aij + (- aij) = 0, то описанная игра является матричной игрой с нулевой суммой.

Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие. Первый и второй игроки бросают монету и в результате выпадает «орёл» или «решка». Если одновременно выпали «орёл» и «орёл» или «решка» или «решка», то первый игрок выиграет одну единицу, а в других случаях он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении второго игрока. Соответствующая платёжная матрица будет следующей:

.

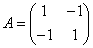
3 Как происходит выбор стратегии в матричной игре?

Вновь посмотрим на платёжную матрицу:

.

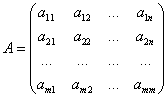
Сначала определим величину выигрыша первого игрока, если он использует i-ю чистую стратегию. Если первый игрок использует i-ю чистую стратегию, то логично предположить, что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим как v1, называется максиминным выигрышем или нижней ценой игры.

Теперь определим величину проигрыша второго игрока, если он использует j-ю стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим как v2, называется минимаксным проигрышем или верхней ценой игры.

Пример 1. Дана матричная игра с платёжной матрицей

.

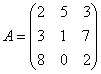
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.

Теперь, когда мы научились находить нижнюю и верхнюю цену игры, максиминную и минимаксную стратегии, пришло время научиться обозначать эти понятия формально.

Итак, гарантированный выигрыш первого игрока: .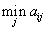

Первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так: .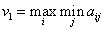

Первый игрок использует такую свою чистую стратегию, чтобы проигрыш второго игрока был максимальным. Этот проигрыш обозначается так: .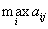

Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был минимальным. Этот проигрыш (минимакс) обозначается так:

.

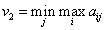
Пример 2. Дана матричная игра с платёжной матрицей

.

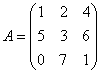
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.

Седловая точка в матричных играх

Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет седловую точку. Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке и наибольшим в столбце и равен цене игры.

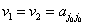
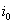
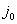
Таким образом, если , то — оптимальная чистая стратегия первого игрока, а — оптимальная чистая стратегия второго игрока. То есть равные между собой нижняя и верхняя цены игры достигаются на одной и той же паре стратегий.

В этом случае матричная игра имеет решение в чистых стратегиях.

Пример 3. Дана матричная игра с платёжной матрицей

.

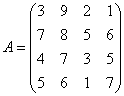
Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?

Дата добавления: 2019-04-03 ; просмотров: 4821 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Заметки с MBC Symposium: еще о седловых точках

Напоследок, о второй части доклада Surya Ganguli — как теоретическое понимание процесса оптимизации может помочь на практике, а именно, какую роль играют седловые точки (первая часть вот тут, и она совершенно необязательна для чтения дальше).

Disclaimer: пост написан на основе отредактированных логов чата closedcircles.com, отсюда и стиль изложения, и уточняющие вопросы.

Чуть-чуть напомню, что такое седловые точки. В пространстве нелинейных функций есть точки с нулевым градиентом по всем координатам — именно к ним стремится градиентный спуск.
Если у точки градиент по всем координатам 0, то она может быть:

Итак, нам рассказывают хорошие новости для градиентного спуска в очень многомерном пространстве (каким является оптимизация весов глубокой нейросети).

Оба этих утверждения были известны и теоретически доказаны для случайных ландшафтов в больших измерениях.
В сотрудничестве с лабой Yoshua Bengio их получилось экспериментально продемонстрировать и для нейросетей (теоретически пока не осилили).

Это гистограмма значений cost function в локальных минимумах, которые получились многократными попытками тренировок из разных точек — чем меньше параметров, тем меньше разброс значений в локальных минимумах. Когда параметров много, разброс резко уменьшается и становится очень близким глобальному минимуму.

Главный вывод — что локальных минимумов бояться не нужно, основные проблемы — с седловыми точками. Раньше, когда мы плохо умели тренировать нейросети, мы думали, что это из-за того, что система скатывается в локальный минимум. Оказывается, нет, мы просто не могли выбраться из седловой точки.

И вот они придумали твик градиентного спуска, который хорошо избегает седловых точек. К сожалению, у них там используется гессиан.

Для необразованных как я, гессиан — это матрица значений попарных вторых производных в точке. Если думать о градиенте как о первой производной для функции от многих переменных, гессиан — вторая.
Александр Власов вот написал хороший туториал про так называемые second order optimizations, к которым относится работа с гессианом.

Разумеется считать гессиан — страшно непрактично для современных нейросетей, поэтому я не знаю как их решение на практике применять.

Второй момент — это они придумали некую теоретически кошерную инициализацию, которая в случае просто линейных систем решает проблему vanishing gradients и дает тренировать сколь угодно глубокую линейную систему за одинаковое количество градиентных шагов.
И мол утверждается, что и для нелинейных систем это тоже помогает. Я, правда, пока не видел упоминаний в литературе успешного использования этой техники.
Ссылки на полные статьи: про оптимизацию градиентного спуска и про улучшенную инициализацию.

Источник

Седловая точка

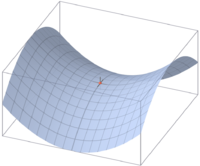
Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. В такой точке, если рассматривается функция двух переменных, образованная графиком функции поверхность обычно напоминает по форме седло или горный перевал — выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний. Например, два холма, между которыми находится высокий перевал, образуют седловую точку в вершине этого перевала: на карте высот это будет выглядеть как центр «восьмерки», образованной соответствующими изолиниями.

Содержание

Седловая точка в математическом анализе

Проверить, является ли данная стационарная точка функции F(x,y) двух переменных седловой, можно, вычислив матрицу Гессе функции в этой точке: если гессиан будет неопределенной квадратичной формой, то данная точка — седловая. Например, составив матрицу Гессе функции в стационарной точке получим матрицу:

которая является неопределенной. Поэтому, точка данной функции — седловая. Однако вышеприведенный критерий предоставляет только достаточное условие наличия седловой точки. Например, является седловой точкой функции , но матрица Гессе в данном случае будет нулевой матрицей, которую, по определению, нельзя назвать неопределенной.

В общем случае, седловой точкой гладкой функции (график которой изображает кривую, поверхность или гиперповерхность) называется такая стационарная точка, в окрестности которой данная кривая/поверхность/гиперповерхность не лежит полностью по одну сторону касательного пространства в данной точке.

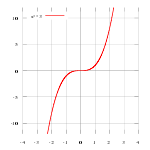
В случае функции одной переменной, седловая точка — такая точка, которая одновременно является и стационарной точкой, и точкой перегиба (точка перегиба не является локальным экстремумом).

Седловая точка матрицы

Седловой точкой (седловым элементом) матрицы называют элемент матрицы , удовлетворяющий условиям , то есть элемент матрицы, который одновременно является минимальным элементом в соответствующей строке матрицы и максимальным элементом в соответствующем столбце матрицы, или же наоборот, то есть элемент матрицы, который одновременно является максимальным элементом в соответствующем столбце матрицы и минимальным элементом в соответствующей строке матрицы.

Примеры

имеет 1 седловой элемент, равный 4, который расположен в первой строке в третьем столбце матрицы, так как он одновременно является минимальным элементом в соответствующей строке матрицы (в данном случае в первой строке матрицы) и максимальным элементом в соответствующем столбце матрицы (в данном случае в третьем столбце матрицы).

имеет 4 седловых элемента, равных 2, которые расположены в первой строке в первом столбце, в первой строке в четвёртом столбце, во второй строке в первом столбце, во второй строке в четвёртом столбце матрицы, соответственно.

Данный пример показывает, что матрица может иметь несколько (более одной) седловых точек.

Если матрица имеет несколько седловых точек, то все их значения равны.

Так, в матрице, все элементы которой равны друг другу, все элементы являются седловыми точками.

не имеет седловой точки.

Применение

Вышеприведенное использование термина «седловая точка» имеет особое значение в теории игр. Так, например, в играх с нулевой суммой седловая точка платёжной матрицы является равновесием Нэша.

См. также

Литература

Полезное

Смотреть что такое «Седловая точка» в других словарях:

Седловая точка — [saddle point] в математическом программировании точка, где функция Лагранжа (см. Лагранжиан) достигает максимума по исходным переменным (прямой задачи) и минимума по множителям Лагранжа. При некоторых условиях в задачах выпуклого и линейного … Экономико-математический словарь

седловая точка — В математическом программировании точка, где функция Лагранжа (см. Лагранжиан) достигает максимума по исходным переменным (прямой задачи) и минимума по множителям Лагранжа. При некоторых условиях в задачах выпуклого и линейного программирования… … Справочник технического переводчика

СЕДЛОВАЯ ТОЧКА — (saddle point) Точка, в которой значение функции двух переменных достигает максимума (maximum) в изменении в одних направлениях и минимума (minimum) в изменении в других направлениях. Термин заимствован из географии, где седло – низшая точка в… … Экономический словарь

СЕДЛОВАЯ ТОЧКА — точка гладкой поверхности, вблизи к рой поверхность лежит по разные стороны от своей касательной плоскости. Если С. т. является точкой двукратно непрерывно дифференцируемой поверхности, то ее гауссова кривизна в этой точке неположительна. С. т.… … Математическая энциклопедия

Седловая точка — SADDLE POINT 1. Такое сочетание значений переменных величин в функции, при котором получающееся в результате значение функции является максимальным в одном измерении и минимальным в другом. Рассмотрим функцию Y = f(Х, Z). Если показатель Y… … Словарь-справочник по экономике

точка равновесия — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] точка равновесия Такая точка в пространстве координат системы, которая характеризует ее состояние равновесия в… … Справочник технического переводчика

Точка равновесия — [equilib­rium point] такая точка в пространстве координат системы, которая характеризует ее состояние равновесия в данный момент. Это одна из стационарных точек функции, описывающей поведение системы, таким образом все частные производные функции … Экономико-математический словарь

Стационарная точка — [statio­nary point] точка, в которой все частные производные первого порядка рассматриваемой функции от нескольких переменных равны нулю и тем самым градиент дифференцируемой функции обращается в нуль. Любая экстремальная точка (экстремум)… … Экономико-математический словарь

КООРДИНАТА РЕАКЦИИ — величина, характеризующая изменение многоатомной системы в процессе ее хим. превращ. из реагентов в продукты р ции. Определение К. р. тесно связано с топографией поверхности потенциальной энергии (ППЭ) U(qi), к рая является ф цией Nвнутр.… … Химическая энциклопедия

Источник

СЕДЛОВАЯ ТОЧКА

(в теории игр) функции F,заданной на декартовом произведении двух множеств ,- точка , для к-рой

Наличие С. т. у функции Fравносильно существованию оптимальных стратегий у игроков в антагонистической игре Г=( Х, Y, F). В.

Смотреть что такое «СЕДЛОВАЯ ТОЧКА» в других словарях:

Седловая точка — функции z=x2 y2 (обозначена красным) … Википедия

Седловая точка — [saddle point] в математическом программировании точка, где функция Лагранжа (см. Лагранжиан) достигает максимума по исходным переменным (прямой задачи) и минимума по множителям Лагранжа. При некоторых условиях в задачах выпуклого и линейного … Экономико-математический словарь

седловая точка — В математическом программировании точка, где функция Лагранжа (см. Лагранжиан) достигает максимума по исходным переменным (прямой задачи) и минимума по множителям Лагранжа. При некоторых условиях в задачах выпуклого и линейного программирования… … Справочник технического переводчика

СЕДЛОВАЯ ТОЧКА — (saddle point) Точка, в которой значение функции двух переменных достигает максимума (maximum) в изменении в одних направлениях и минимума (minimum) в изменении в других направлениях. Термин заимствован из географии, где седло – низшая точка в… … Экономический словарь

СЕДЛОВАЯ ТОЧКА — точка гладкой поверхности, вблизи к рой поверхность лежит по разные стороны от своей касательной плоскости. Если С. т. является точкой двукратно непрерывно дифференцируемой поверхности, то ее гауссова кривизна в этой точке неположительна. С. т.… … Математическая энциклопедия

Седловая точка — SADDLE POINT 1. Такое сочетание значений переменных величин в функции, при котором получающееся в результате значение функции является максимальным в одном измерении и минимальным в другом. Рассмотрим функцию Y = f(Х, Z). Если показатель Y… … Словарь-справочник по экономике

точка равновесия — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] точка равновесия Такая точка в пространстве координат системы, которая характеризует ее состояние равновесия в… … Справочник технического переводчика

Точка равновесия — [equilib­rium point] такая точка в пространстве координат системы, которая характеризует ее состояние равновесия в данный момент. Это одна из стационарных точек функции, описывающей поведение системы, таким образом все частные производные функции … Экономико-математический словарь

Стационарная точка — [statio­nary point] точка, в которой все частные производные первого порядка рассматриваемой функции от нескольких переменных равны нулю и тем самым градиент дифференцируемой функции обращается в нуль. Любая экстремальная точка (экстремум)… … Экономико-математический словарь

КООРДИНАТА РЕАКЦИИ — величина, характеризующая изменение многоатомной системы в процессе ее хим. превращ. из реагентов в продукты р ции. Определение К. р. тесно связано с топографией поверхности потенциальной энергии (ППЭ) U(qi), к рая является ф цией Nвнутр.… … Химическая энциклопедия

Источник